Unit Circle Calculator

Q: What is a unit circle?

A unit circle is a circle with a radius of 1 (unit radius). In most cases, it is centered at the point ( 0 , 0 ) (0,0) ( 0 , 0 ) , the origin of the coordinate system. The unit circle is a really useful concept when learning trigonometry and angle conversion.

Q: What is tan 30 using the unit circle?

tan 30° = 1/√3 . To find this answer on the unit circle, we start by finding the sin and cos values as the y-coordinate and x-coordinate, respectively: sin 30° = 1/2 and cos 30° = √3/2 . Now use the formula. Recall that tan 30° = sin 30° / cos 30° = (1/2) / (√3/2) = 1/√3 , as claimed. See how easy it is?

Q: How do I find cosecant with the unit circle?

To determine the cosecant of θ on the unit circle: From the center of the circle draw the radius corresponding to the angle θ . Draw tangent lines to the circle at points (0,1) and (0,-1) . Extend the radius from Step 1 so that it intersects one of those tangents. The distance from the center to the intersection point from Step 3 is the cosecant of your angle θ . If there's no intersection point, the cosecant of θ is undefined (this happens when sin θ = 0 ).

Q: How do I find arcsin 1/2 with the unit circle?

As the arcsine is the inverse of the sine function , finding arcsin(1/2) is equivalent to finding an angle whose sine equals 1/2 . On the unit circle, the values of sine are the y-coordinates of the points on the circle. Inspecting the unit circle, we see that the y-coordinate equals 1/2 for the angle π/6 , i.e., 30° .

Created by Hanna Pamuła, PhD

Reviewed by Dominik Czernia, PhD and Jack Bowater

Last updated: Jul 01, 2024

Table of contents:

Welcome to the unit circle calculator ⭕. Our tool will help you determine the coordinates of any point on the unit circle. Just enter the angle ∡, and we'll show you sine and cosine of your angle.

If you're not sure what a unit circle is, scroll down, and you'll find the answer. The unit circle chart and an explanation on how to find unit circle tangent, sine, and cosine are also here, so don't wait any longer – read on in this fundamental trigonometry calculator!

What is a unit circle?

A unit circle is a circle with a radius of 1 (unit radius). In most cases, it is centered at the point $(0,0)$ , the origin of the coordinate system.

The unit circle is a really useful concept when learning trigonometry and angle conversion.

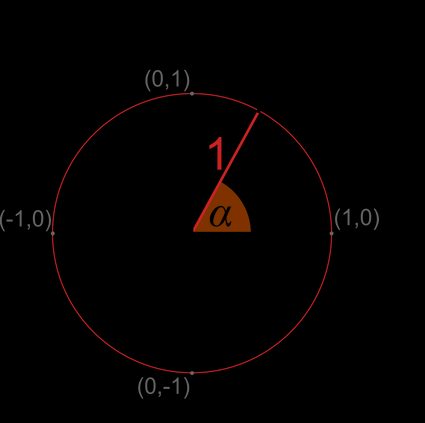
Now that you know what a unit circle is, let's proceed to the relations in the unit circle.

Unit circle: sine and cosine

OK, so why is the unit circle so useful in trigonometry?

TL;DR

Unit circle relations for sine and cosine:

Sine is the y-coordinate; and
Cosine is the x-coordinate

🙋 Do you need an introduction to sine and cosine? Visit our sine calculator and cosine calculator!

Standard explanation:

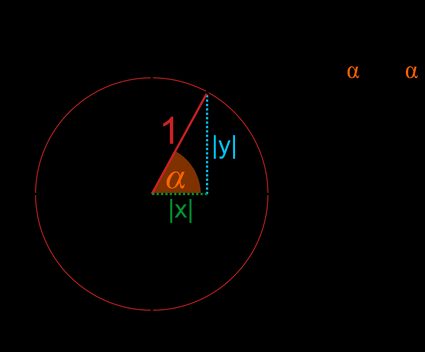
Let's take any point A on the unit circle's circumference.

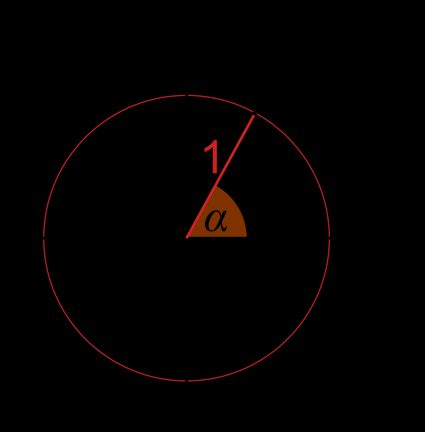
Unit circle in a coordinate system, with point A(x,y)

The coordinates of this point are $x$ and $y$ . As it's a unit circle, the radius r is equal to $1$ (a distance between point $P$ and the center of the circle).

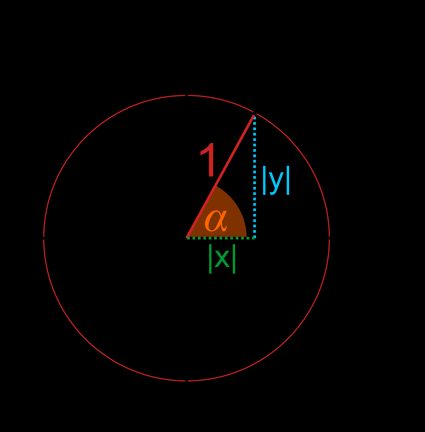
Unit circle in a coordinate system with point A(x,y) and legs |x| and |y|

By projecting the radius onto the x and y axes, we'll get a right triangle, where $|x|$ and $|y|$ are the lengths of the legs, and the hypotenuse is equal to $1$ .

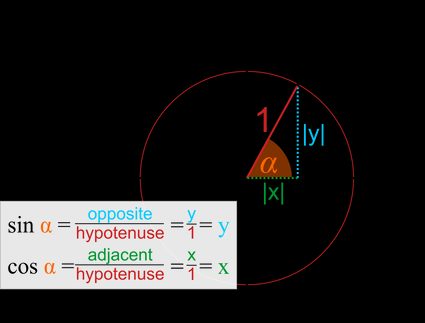
Unit circle in a coordinate system with sine and cosine formulas.

As in every right triangle, you can determine the values of the trigonometric functions by finding the side ratios:

\sin(\alpha)=\frac{\mathrm{opposite}}{\mathrm{hypotenuse}} = \frac{y}{1} = y

So, in other words, sine is the y-coordinate:

\cos(\alpha) = \frac{\mathrm{adjacent}}{\mathrm{hypotenuse}} = \frac{x}{1} = x

And cosine is the x-coordinate.

Unit circle in a coordinate system with point A(x,y) = (cos a, sin a)

The equation of the unit circle, coming directly from the Pythagorean theorem, looks as follows:

x^2+y^2=1

Or, analogically:

\sin^2(\alpha) + \cos^2(\alpha) = 1

🙋 For an in-depth analysis, we created the tangent calculator!

This intimate connection between trigonometry and triangles can't be more surprising! Find more about those important concepts at Omni's right triangle calculator.

Unit circle tangent & other trig functions

You can find the unit circle tangent value directly if you remember the tangent definition:

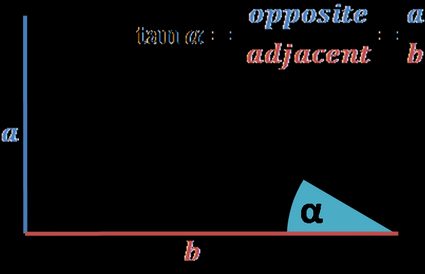
Right triangle: illustration of the tangent definition. Opposite side over an adjacent.

The ratio of the opposite and adjacent sides to an angle in a right-angled triangle.

\tan{\alpha} = \frac{\mathrm{opposite}}{\mathrm{adjacent}}

As we learned from the previous paragraph, $\sin(\alpha) = y$ and $\cos(\alpha) = x$ , so:

\tan(\alpha) = \frac{y}{x}

We can also define the tangent of the angle as its sine divided by its cosine:

\tan(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)} = \frac{y}{x}

Which, of course, will give us the same result.

Another method is using our unit circle calculator, of course. 😁

But what if you're not satisfied with just this value, and you'd like to actually to see that tangent value on your unit circle?

It is a bit more tricky than determining sine and cosine – which are simply the coordinates. There are two ways to show unit circle tangent:

Method 1:

Create a tangent line at point $A$ .
It will intersect the x-axis in point $B$ .
The length of the $\bar{AB}$ segment is the tangent value

Method 2:

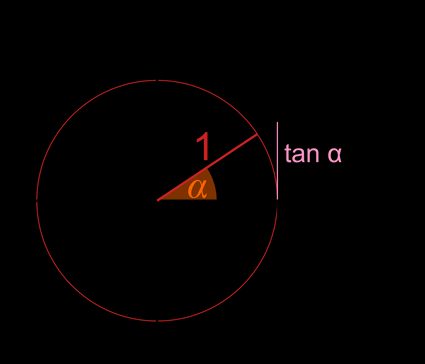
Draw a line $x = 1$ .
Extend the line containing the radius.
Name the intersection of these two lines as point $C$ .
The tangent, $\tan(\alpha)$ , is the y-coordinate of the point $C$ .

In both methods, we've created right triangles with their adjacent side equal to 1 😎

Sine, cosine, and tangent are not the only functions you can construct on the unit circle. Apart from the tangent cofunction – cotangent – you can also present other less known functions, e.g., secant, cosecant, and archaic versine:

Trigonometric functions based on the circle — Graphic by Steven G. Johnson at English Wikipedia, CC BY-SA.

Unit circle chart – unit circle in radians and degrees

The unit circle concept is very important because you can use it to find the sine and cosine of any angle. We present some commonly encountered angles in the unit circle chart below:

As an example – how to determine $\sin(150\degree)$ ?

Search for the angle $150\degree$ .
As we learned before – sine is a y-coordinate, so we take the second coordinate from the corresponding point on the unit circle:

\qquad \sin(150\degree) = \frac{1}{2}

Alternatively, enter the angle 150° into our unit circle calculator. We'll show you the $\sin(150\degree)$ value of your y-coordinate, as well as the cosine, tangent, and unit circle chart.

How to memorize unit circle?

Well, it depends what you want to memorize 🙃 There are two things to remember when it comes to the unit circle:

Angle conversion, so how to change between an angle in degrees and one in terms of $\pi$ (unit circle radians); and
The trigonometric functions of the popular angles.

Let's start with the easier first part. The most important angles are those that you'll use all the time:

$30\degree = \pi/6$ ;
$45\degree = \pi/4$ ;
$60\degree = \pi/3$ ;
$90\degree = \pi/2$ ; and
Full angle, $360\degree = 2\pi$ .

As these angles are very common, try to learn them by heart ❤️. For any other angle, you can use the formula for angle conversion:

\alpha\ [\mathrm{rad}] = \frac{\pi}{180\degree}\times \alpha\ [\mathrm{deg}]

Conversion of the unit circle's radians to degrees shouldn't be a problem anymore! 💪

The other part – remembering the whole unit circle chart, with sine and cosine values – is a slightly longer process. We won't describe it here, but feel free to check out 3 essential tips on how to remember the unit circle or this WikiHow page. If you prefer watching videos 🖥️ to reading 📘, watch one of these two videos explaining how to memorize the unit circle:

A Trick to Remember Values on The Unit Circle; and
How to memorize unit circle in minutes!!

Also, this table with commonly used angles might come in handy:

$\mathrm{\boldsymbol{\alpha}}$ (angle)		Trigonometric functions
$\mathrm{deg}$	$\mathrm{rad}$	$\sin(\alpha)$	$\cos(\alpha)$	$\tan(\alpha)$
$30\degree$	$\pi/6$	$1/2$	$\sqrt{3}/2$	$\sqrt{3}/3$
$45\degree$	$\pi/4$	$\sqrt{2}/2$	$\sqrt{2}/2$	$1$
$60\degree$	$\pi/3$	$\sqrt{3}/2$	$1/2$	$\sqrt{3}$

And if any methods fail, feel free to use our unit circle calculator – it's here for you, forever ❤️ Hopefully, playing with the tool will help you understand and memorize the unit circle values!

FAQ

What is tan 30 using the unit circle?

tan 30° = 1/√3. To find this answer on the unit circle, we start by finding the sin and cos values as the y-coordinate and x-coordinate, respectively: sin 30° = 1/2 and cos 30° = √3/2. Now use the formula. Recall that tan 30° = sin 30° / cos 30° = (1/2) / (√3/2) = 1/√3, as claimed. See how easy it is?

How do I find cosecant with the unit circle?

To determine the cosecant of θ on the unit circle:

From the center of the circle draw the radius corresponding to the angle θ.
Draw tangent lines to the circle at points (0,1) and (0,-1).
Extend the radius from Step 1 so that it intersects one of those tangents.
The distance from the center to the intersection point from Step 3 is the cosecant of your angle θ.
If there's no intersection point, the cosecant of θ is undefined (this happens when sin θ = 0).

How do I find arcsin 1/2 with the unit circle?

As the arcsine is the inverse of the sine function, finding arcsin(1/2) is equivalent to finding an angle whose sine equals 1/2. On the unit circle, the values of sine are the y-coordinates of the points on the circle. Inspecting the unit circle, we see that the y-coordinate equals 1/2 for the angle π/6, i.e., 30°.

Hanna Pamuła, PhD

Unit circle in a coordinate system with Pythagorean trig identity formula.

Angle

ArccosArcsinArctan… 18 more