Equation of a Sphere Calculator

Our equation of a sphere calculator will help you write the equation of a sphere in the standard form or expanded form if you know the center and radius of the sphere. Alternatively, you can find the sphere equation if you know its center and any point on its surface or if you know the end-points of any of its diameters. This calculator can also find the center and radius of a sphere from its equation.

Are you wondering what is the standard equation of a sphere or how to find the center and radius of a sphere using its equation? Have you perhaps come across a sphere equation that doesn't look like the general equation? Are you curious how knowing the diameter's end-points or the center and a point on the sphere can help you find the sphere's equation? Grab your favorite drink and keep reading this article; we'll tackle these questions together!

This calculator can also determine a sphere's surface area and volume from its equation. Want to calculate them without bothering with the sphere equation? Head to our sphere calc!

The equation of a sphere in the standard form is given by:

where:

• $(x,y,z)$ – Coordinates of any point lying on the surface of the sphere;
• $(h,k,l)$ – Coordinates of the center of the sphere; and
• $r$ – Radius of the sphere.

If we know the center and radius of the sphere, we can plug them into this standard form to obtain the equation of the sphere. For example, consider a sphere with a radius of $10$ and its center at $(3,7,5)$. By inserting this into the equation above, we get the standard equation of the sphere:

Similarly, you can use the standard form of the sphere equation to find the radius and center of the sphere. For example, a sphere with the equation $(x-7)^2 + (y-12)^2 + (z-4)^2 = 36$ would have its center at $(7,12,4)$, and its radius is given by:

Now that we know the standard equation of a sphere, let's learn how it came to be:

1. First thing to understand is that the equation of a sphere represents all the points lying equidistant from a center point. In other words, any point that lies at a distance $r$ from a point $(h,k,l)$ lies on the sphere. Sound familiar? A circle equation works the same way! Go to our equation of a circle calculator and see if you can uncover more similarities!
2. Consider a point $S(x,y,z)$ that lies at a distance $r$ from the center $(h,k,l)$. Using distance formula, we get:

3. Squaring on both sides and rearranging this equation, we get:

And, voila! Just like that, we got the standard equation of a sphere! It bears repeating that every point $S$ that satisfies this equation lies on the surface of the sphere.

Sometimes, you may come across a sphere equation that appears different from the standard form we've discussed so far. Generally, such equations should look like the following:

where:

• $E$ – Sum of all coefficients of the $x$ terms;
• $F$ – Sum of all coefficients of the $y$ terms;
• $G$ – Sum of all coefficients of the $z$ terms; and
• $H$ – Sum of all constants terms.

This equation may seem intimidating at a glance, but if you take a closer look; it is simply the expanded version of the standard form we're used to. Let's use the completing the squares method to backtrack our way from the expanded version to the simpler, standard form:

1. Rearrange the equation for clarity:

2. To write $(x^2+Ex)$ in the $(a-b)^2 = a^2-2ab+b^2$ format, we need to identify $a$ and $b$. Clearly, $a=x$. If $-2ab = Ex$, we get:

3. Adding and subtracting the quantity $\textcolor{red}{\left(- \frac{E}{2} \right)^2}$ to the equation, we get:

4. Similarly, we complete the squares for the y-terms and z-terms by adding and subtracting the quantities $\textcolor{red}{\left(- \frac{F}{2} \right)^2}$ and $\textcolor{red}{\left(- \frac{G}{2} \right)^2}$ to get:

5. Rearrange the equation to group all the constant terms on the right-hand side:

6. Comparing this equation with the standard form of the sphere equation $(x-h)^2 +(y-k)^2 + (z-l)^2) = r^2\text{:}$

7. Extracting the center point and radius of the sphere from this equation, we get:

Need help completing the squares? Our completing the square calculator will serve you.

In this sphere equation calculator, you can simply select the expanded form option as the type of the equation and enter the corresponding $E$, $F$, $G$ and $H$ values to obtain the equation in the standard form, its center and radius, and other relevant information.

Now that you know what the equation of a sphere is, let's discuss how to obtain it in cases where you don't have the necessary parameters readily available. Suppose you only know the end-points of any one of the diameters of the sphere and have no information on the center point or radius. You still have a way to frame its equation.

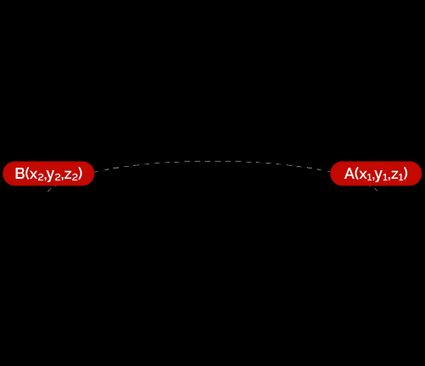
Say the diameter $AB$ of the sphere has the endpoints $A(x_1,y_1,z_1)$ and $B(x_2,y_2,z_2)$. Clearly, the center $C(h,k,l)$ is given by the mid-point of $AB$, which is given by:

Once we know the center, we can obtain the radius as the distance $CA$ or $CB$, through the distance formula:

We can then insert this center and radius in the standard sphere equation.

Similar to the case above, if we know the center $(h,k,l)$ and any point $P(p_x,p_y,p_z)$ on the sphere, we can use the distance formula to obtain the radius:

Again, we can directly plug in the values for the center and the radius in the standard equation of a sphere.

You can use this equation of a sphere calculator to find the sphere equation or to find the center and radius of the sphere, depending on the variables you already know:

• If you have the center and radius, directly enter them in the center coordinates and radius fields to get the sphere equation in the standard form and expanded form.

• If you know the equation of the sphere in the standard form, choose the standard equation type from the Select equation field. Enter the $h$, $k$, and $l$ values in the corresponding fields, along with the remaining constant $r^2$ value in the $R$ field, to calculate the center and radius of the sphere.

• If you know the equation of the sphere in the expanded form, choose the expanded equation type from the Select equation field. Enter the values for x-term coefficients in the $E$ field, for y-term coefficients in the $F$ field, for the z-term coefficients in the $G$ field, and the remaining constant term in the $H$ field to calculate the center and radius of the sphere.

• If you know the endpoints of any diameter of the sphere, choose "Known endpoints of diameter AB" from the Select equation field and enter the endpoints to get the equation of the sphere along with its center and radius.

• If you know the center and any point on the sphere, choose "Known point on the sphere $P(p_x,p_y,p_z)$" from the Select equation field and enter the point coordinates and center coordinates to obtain the equation of the sphere and its radius.

• Once you know the sphere's radius, obtaining other relevant properties such as area is straightforward. This calculator will evaluate the surface area and volume of the sphere for your convenience.

• If you're having problems with the calculator, specifically if the tool ignores your inputs, try refreshing the calculator and enter values again in that specific calculator mode. You can do this by clicking on the circular reload icon at the very bottom of the tool.