Completing the Square Calculator

This calculator for completing the square solves any given quadratic equation in the form ax² + bx + c = 0 with help from the method known as... "completing the square" 😉 Below, we give a detailed example of how to complete the square and then explain geometrically the steps of completing the square.

As a by-product, we will also derive the well-known quadratic formula (used in our quadratic formula calculator), and if by completing the square you mean filling a square with numbers, why not try our magic square calculator?

You just need to enter the coefficients of the quadratic equation:

ax² + bx + c = 0

...you want to solve. Remember that a can't be zero (otherwise, your equation is linear instead of quadratic).

Our completing the square calculator not only solves the equation but also shows you the steps of how to complete the square.

Go to the Complex number mode and Precision options of this completing the square calculator if you want to:

• Allow complex roots, i.e., equation roots represented by complex numbers (by default, only real roots are displayed).
• Increase the precision with which non-integer coefficients are computed.

Let's take the equation

x² + 6x - 7 = 0

and solve it by completing the square. We break the process into several simple steps so that nobody gets overwhelmed by the formula for completing the square:

1. Add 7 to either side of the equation so that the left-hand side contains only terms with x:

   x² + 6x - 7 + 7 = 7
x² + 6x = 7

2. Now it's time to complete the square! Take one-half of the coefficient in front of x and square it:

   • the coefficient in front of x is 6

   • one half of 6 is 3

   • after squaring, we get 3² = 9

3. Add the number computed in Step 2 to both sides of the equation:

   x² + 6x + 9 = 7 + 9
x² + 6x + 9 = 16

4. Recall the short multiplication formula, (p + q)² = p² + 2pq + q², and note that we may apply it 'backwards' to the left-hand side of our equation (with p = x and q = 3). We obtain:

   (x + 3)² = 16

5. Take the calculate the square root:

   x + 3 = 4 or x + 3 = - 4

   which gives:

   x = 1; and x = - 7

Hence, we've found the solutions of x² + 6x - 7 = 0.

This means we've determined the points where the parabola y = x² + 6x - 7 intersects the x-axis.

• What if a ≠ 1?

  In the example above, it is important that the coefficient in front of x² is equal to 1. What do you do if you are asked to solve a quadratic equation where a ≠ 1? Just apply one of the most frequently used problem-solving techniques in math, namely... transform the problem to some you've already solved🙃 What does that mean in our context? Just divide your equation by a!

  For example: assume we have to solve

  2x² + 12x - 5 = 0

  by completing the square. We see that a = 2. Dividing either side by 2, we obtain

  x² + 6x - 2.5 = 0

  and so the coefficient in front of x² is equal to 1. Now just go ahead with the steps we explained in the example above.

• What if b = 0?

  If b=0, then you may skip Steps 2, 3, and 4 and go from x² = -c (Step 1) directly to x = ±√|c| (Step 5).

  Why?

  Because in Step 2, we take b and perform some arithmetic operations on it, which gives us the number with which we will 'complete the square.'
  Note that if b = 0, then (b/2)² = 0, and so we would add 0 to both sides of the equations. This is, of course, redundant.

Let's go once again through the steps for completing the square. This time we apply it to the general equation
x² + bx + c = 0

• Note that we've already made sure that a = 1

• Move c to the right-hand side: x² + bx = -c

• x² is the area of the square with side x

• bx is the area of the rectangle of sides x and b

• Let the magic happen:

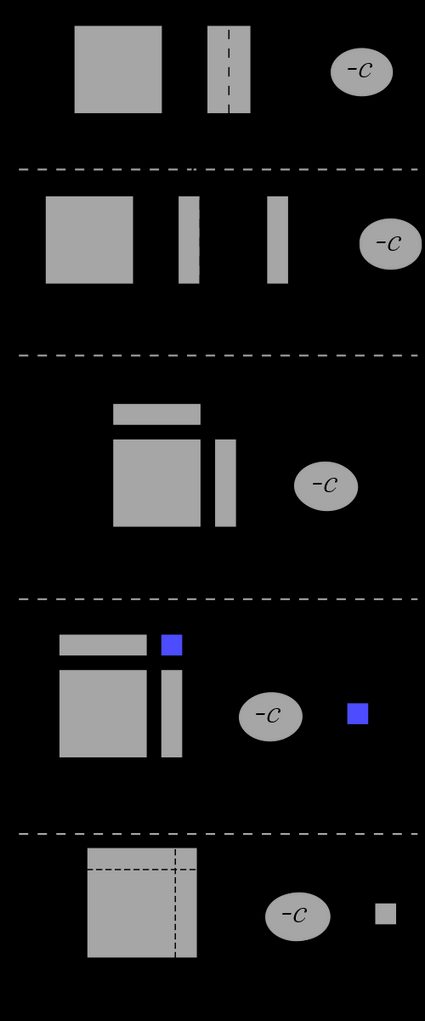
As a consequence, we have

(x + b/2)² = -c + b²/4

Taking the square root and moving b/2 to the right-hand side, we get:

• x = -b/2 ± √(-c + b²/4) if b²/4 > c; in such a case, the equation has two distinct real roots.

• x = -b/2 if b²/4 = c: the equation has one real root.

• the equation has no real roots if b²/4 < c. If we allow complex roots, they are given by x = -b/2 ± i √(c - b²/4).