Gamma Function Calculator
Our Gamma function calculator uses the best Gamma function approximations to help you find the value of the Gamma function for both real and complex arguments.
Scroll down if you are unsure what the Gamma function formula is or how to calculate the Gamma function at a particular point. We will explain the link between the Gamma function and factorials, give you the Gamma function integral formula and, since a picture is worth a thousand words, show a few graphs of the Gamma function.
What is the Gamma function? Gamma function properties
The Gamma function is very tightly linked to the notion of factorial. Hence, before moving on to the Gamma function properties, let us first recall what the factorial is.
Factorial operator
Let n be a positive integer. The factorial of n (denoted by n!) is the product of all integers between (and including) 1 and n:
n! = 1 ⋅ 2 ⋅ ... ⋅ (n-1) ⋅ n.
For instance
5! = 1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5 = 120.
Factorials are essential in statistics and probability, and they have many uses. For example, you can find factorials present in the following calculators:
If you want to learn more about factorials, especially their applications, visit our dedicated factorial calculator.
What is essential for us is the fact that the factorial is only defined for positive integers. Is there any way to extend the factorial to all positive numbers? How about all real (or even complex) numbers? We can think of this as the following interpolation problem:
Can we find a smooth curve that connects the points
(x, y)given byy = x!at the positive integer values for x?
There have been several approaches to solving this problem, and the Gamma function is the most popular one.
Gamma function and factorials
Gamma is a function (denoted by the Greek letter 𝚪) that allows us to extend the notion of factorial well beyond positive integer numbers. Formally, the Gamma function formula is given by an integral (see the next section for more details). Most importantly, the Gamma function and factorials are linked via the relationship:
𝚪(n) = (n - 1)!
So it is indeed a solution to the interpolation problem described above. Below you can see the graph of the Gamma function 𝚪(n + 1) = n! for all positive numbers (the red dots are the values of the factorial at each integer of x):
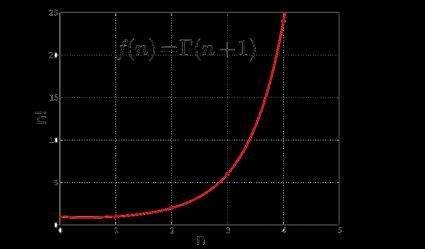
💡 Do you know that... this function was defined by the Swiss mathematician Leonhard Euler in the first half of the 18th century, while the name Gamma and notation 𝚪 was introduced by the French mathematician Adrien-Marie Legendre at the beginning of the 19th century.
Gamma function – integral formula
For more advanced readers, we now briefly discuss the Gamma function integral formula and show some more Gamma function properties. Namely, for a complex number z taken from the positive complex half-plane (i.e., for z with a positive real part), we define the Gamma function via the following integral:

This Gamma function integral is absolutely convergent. With the help of standard integration methods, we can also show that:
𝚪(1) = 1 and 𝚪(z + 1) = z × 𝚪(z).
In consequence, we get 𝚪(n) = (n − 1)! for any natural number n. Hence, we've extended the factorial to the positive complex half-plane.
If Re(z) ≤ 0, then the above integral is not convergent, but 𝚪 has a unique analytic continuation to the negative half-plane. To find this analytic continuation, we can use the formula:
𝚪(z) = 𝚪(z+1) / z.
However, this technique works if and only if z is a non-positive integer. Therefore, we must leave the Gamma function undefined at these integers to avoid dividing by zero. So, we've extended the factorial to the whole complex plane, except non-positive integers.
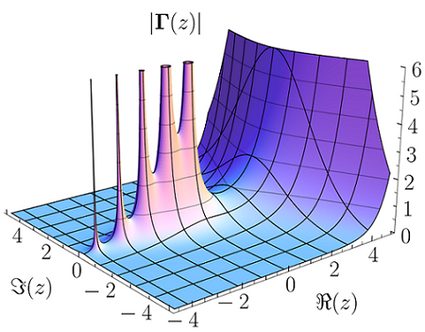
The Gamma function graph plotted over the real numbers looks like this:

In the language of complex analysis, we say that Gamma is a meromorphic function in the whole complex plane. At each non-positive integer it has a simple pole and the residue at -n is equal to (-1)ⁿ/n! for n = 0, 1, 2, .... Gamma has no zeros. Here is the plot of the absolute value of Gamma over the complex plane:
How to calculate the Gamma function? Gamma function of 1/2
You now know what the Gamma function is and what the Gamma function formula looks like, but you probably still have very little idea of how to determine its values. Well, we don't have good news for you: it's highly non-trivial to find the values of Gamma, apart from some very specific points, like the Gamma function of 1/2.
Let's start with the simplest case. We've already seen that for positive-integer arguments we have
𝚪(n) = (n − 1)!
so we easily get
𝚪(1) = 0! = 1
𝚪(2) = 1! = 1
𝚪(3) = 2! = 2
𝚪(4) = 3! = 6
etc.
Next, we have a nice formula for half-integer arguments:
𝚪(n/2) = (n-2)!! × √(π/2(n-1))
where n!! is a double factorial. Recall that the double factorial is defined as the product of all integers between 1 and n with the same parity as n: if n is even, then n!! = 2 ⋅ 4 ⋅ ... ⋅ n; and if n is odd, then n!! = 1 ⋅ 3 ⋅ ... ⋅ n.
Using this half-integer formula, we obtain the Gamma function of 1/2:
𝚪(1/2) = √π,
and other fractions:
𝚪(3/2) = 1/2 ⋅ √π
𝚪(5/2) = 3/4 ⋅ √π
etc.
There are also formulas that link the values of Gamma at several points. Thanks to them, you can find the value of Gamma at some point z provided that you know its value at some other point linked to z. For instance, if z is not an integer, then 𝚪(1-z) and 𝚪(z) are linked by Euler's reflection formula:
𝚪(1-z) ⋅ 𝚪(z) = π / sin(π × z).
Thanks to this formula, we find:
𝚪(-1/2) = -2 × √π
𝚪(-3/2) = 4/3 × √π
𝚪(-5/2) = -8/15 × √π
etc.
The reflection formula allows us also to derive the following relationships:
𝚪(1/3) ⋅ 𝚪(2/3) = 2√3/3 × π
𝚪(1/4) ⋅ 𝚪(3/4) = √2 × π
etc.
Unfortunately, no simple expression for 𝚪(1/3) or 𝚪(1/4) exists.
Another interesting formula is the Legendre duplication formula. Assume that 2 × z is not equal to any non-positive integer. Then, if you know any two from 𝚪(z), 𝚪(2 × z), and 𝚪(z + 1/2), you can find the third one. The equation that links all three is of the form:
𝚪(z) ⋅ 𝚪(z + 1/2) = 21 - 2×z × √π × 𝚪(2 × z)
How to use this Gamma function calculator?
Are you still wondering how to calculate the Gamma function? Well, the best answer is: use our Gamma function calculator! Here we briefly describe how to use it:
- Choose the type of argument you want our Gamma function calculator to use. By default, we set it to real arguments, but complex numbers are available as well.
- Enter the argument in the appropriate field(s).
- The calculator uses very precise Gamma function approximations to determine the result. It appears just beneath the argument. Enjoy!
- If you need to increase the precision of calculations, you can increase the number of significant figures using the 'Precision' variable. By default, this Gamma function calculator uses five significant figures to display the result.
Gamma function approximations
As we have seen above, we can find precise values of the Gamma function for only very specific arguments. Fortunately, we can approximate Gamma numerically with arbitrary precision.
There are several Gamma function approximations, let us mention the most popular ones:
Stirling's and Lanczos' methods allow us to compute the values of Gamma with any precision we want, but they still require quite complicated calculations. Our Gamma function calculator uses the Lanczos approximation for small values and an extended Stirling approximation for large values.
Nemes' approximation leads to the

which is, however, a bit less precise. Feel free to use it when accuracy is not critical.