Factorial Calculator

Welcome to the factorial calculator: a tool that calculates the factorial of any number from 0 to 170. On top of calculating, e.g., the 0-factorial or 5-factorial... we will also show you how to use the exclamation point in maths, provide information about the n-factorial formula and the applications it can have. By the end of this, we will have an answer to "what is a factorial?" using the factorial definition. And finally, we will dive into the maths behind it to find how we can include more than just positive integers by using the gamma function.

When you saw an exclamation point in maths for the first time, you probably got shocked or even thought that there was some kind of mistake or typo. But the reality is different: this exclamation point in maths is called the factorial or n-factorial. The factorial is a reasonably unknown operator that can, in fact, be viewed more as an abbreviation than an actual operator, at least at the beginning.

It is important not to confuse the factorial with the prime factorization of a number, which is a way of obtaining the prime numbers that, when multiplied together, give your number. Prime factorization has its uses in maths and is arguably more well-known than the n-factorial. Part of the reason for the popularity of prime factorization is its usefulness when calculating Greatest Common Factor (GCM) and the Least Common Multiplier (LCM), but we digress. However, if you'd like to follow the white rabbit, you can find more information in the prime factorization calculator.

To understand what the factorial does or means, we should start with an example. We could choose any number n and calculate its n-factorial value, but it's best to choose a relatively small number, so let's use 5-factorial.

5! = 5 × 4 × 3 × 2 × 1 = 120

From this example, you can see that it is not rocket science, and you might even take a guess at the factorial formula. You can also understand why this exclamation point in maths can be regarded as an abbreviation since it is not a new operation but rather a collection of multiplications. In short, and somewhat informally, we can define the factorial as the multiplication of all the positive integers smaller than and equal to the given number.

Playing a bit with this, we can see that for 5-factorial, we can relate it to the 4-factorial in a straightforward way:

5! = 5 × (4 × 3 × 2 × 1) = 5 × 4!

This kind of relationship between n-factorials with a different n is the basis of the mathematical formula that defines the factorial operation, as we will see in the next section.

The factorial operation is not used everywhere in maths, but it is essential in statistics and probability problems. In those cases, especially when one has to deal with permutations or combinatorics, the n-factorial appears almost all the time. In the following sections of our factorial calculator, we will see real-world examples of problems that require the usage of factorials and the factorial formula.

So far, we have seen a slightly loose answer to the question "what is a factorial?", but we have not given a proper factorial definition. Well, that is precisely the aim of this section: to see and explain the factorial formula and how we can find the factorial definition in a more mathematical way from it.

For a more mathematical description of the factorial formula, let's look at the n-factorial and how it relates to other factorials. In this case, n can be any number. If we look at the previous examples with 5-factorial, we can see that:

5! = 5 × 4! = 5 × (5-1)!

If we now extrapolate that to the n-factorial:

n! = n × (n-1)!

The above is the general factorial formula and is an integral part of the factorial definition. However, we're sure this does not answer all the questions about factorials you may have. For example, what would happen if we take a negative number? When do I stop subtracting numbers? These are valid questions that the factorial formula above doesn't answer, but are fundamental for having a proper factorial definition.

These two questions can be answered easily by stating that the factorial formula is only defined for positive integers, which means that we cannot go lower than n = 1. But this also brings up another question: What is the 0-factorial? Since we cannot use this formula, you are forgiven for thinking that this question has no answer, and the whole factorial thing is "fake news". However, there is a 'trick' to get around this: setting the value of the zero-factorial to a number by definition.

And, hence, we arrive at the convention:

0! = 1.

A small disclaimer is needed here since, in maths, things are never as easy as "choose a number and roll with it" there are many complex reasons as to why the value of zero-factorial has been set to one and not any other number. However, explaining these reasons in detail is far beyond the scope of this factorial calculator.

Let's check now some of the value for the n-factorial of several small n, like zero factorial, 3 factorial, 5 factorial. Pay special attention to the value of 0 factorial because it is the most important one, and we will talk more about it later.

• 0! = 1
• 1! = 1
• 2! = 2
• 3! = 6
• 4! = 24
• 5! = 120
• 6! = 720
• 7! = 5040
• 8! = 40,320
• 9! = 362,880
• 10! = 3,628,800

We can see how fast the factorial of a number increases as we use bigger numbers. This is yet another situation where scientific notation can save the day (if we know how to truncate to the necessary significant figures correctly) if you need to work with such big numbers. For factorials of numbers greater than 10, don't hesitate to use the factorial calculator above. Besides, you can use logarithms for the computation of factorials of higher numbers. To see how, you may like to check our logarithm calculator where we explain how logarithm can be applied for such arithmetic.

The 0-factorial is a key part of the factorial definition. To understand why it is so important, we can show the problems we encounter when we try to calculate it using the factorial formula above:

0! = 0 × (0-1)!

It looks like no matter what the value of (0-1)! turns out to be, the result should always be 0! = 0, but things are more complicated than that in maths. In the previous section, we saw that the n-factorial is only defined for n > 0, so we have a problem here. The term (0-1)! is what mathematicians call: undefined expression, which means that the expression is not correct, and thus it has no mathematical meaning. This problem is the same as with division by zero. It's not that we cannot calculate it. The problem is that the expression doesn't make sense, it doesn't have a meaning.

This is a reason why 0! is critical to define as a convention value. Setting it's value to 0! = 0 would not be a good idea since it would mean that n! = 0 for any value of n. You can see why by applying the factorial formula. On the other hand, if we set zero-factorial to 1, we now retain the expected values for n-factorial while having a simple convention for the value of 0!.

In the following section, we will see another reason for setting zero-factorial to be equal to 1, with a bit more mathematical logic behind it. In doing that, we will also introduce the Gamma function, which is, in plain terms, an extended factorial formula that includes all positive numbers and the 0-factorial.

It is possible to determine the factorial of non-integer numbers – in fact, it is possible for all real and complex numbers, excluding negative integers. It requires the use of sophisticated mathematical tools, so we will try to give a more straightforward version here, retaining as much accuracy as possible. There have been several approaches to extending the factorial formula to include all positive numbers, each with subtle differences and mostly compatible with each other.

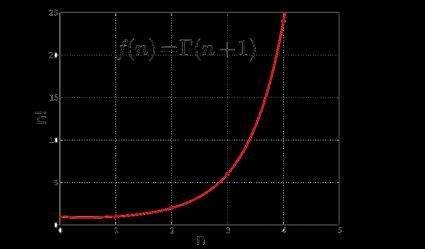
Let's start with the Gamma function. The Gamma function is a function that extends the notion of the n-factorial beyond integers. Obviously, the formula cannot be the same as we have used before because we would end up at a dead-end. In fact, this function extends the n-factorial to complex numbers as well, where the intuitive notion of a factorial is much harder to grasp. The only numbers for which the Gamma function is not defined are negative integers:

𝚪(z) = ∫tᶻ⁻¹ e⁻ᵗ dt

That's the Gamma function's definition, where t is the variable of integration from zero to infinity, and z is a (non-negative-integer) complex number. This formula is reduced to the n-factorial formula when applied over any positive integer n.

n! = 𝚪(n+1)

You can see 2 things from this formula:

1. The Gamma function is much more complicated to use than the n-factorial formula for integers.
2. It is not an exact copy of the n-factorial since you need to calculate the Gamma function's value for n+1 to obtain n!.

To remedy the second "problem", we can introduce the Pi function.

𝚷(z) = ∫tᶻ e⁻ᵗ dt

The Pi function is very similar to the Gamma function but shifted just enough so that the factorial and the function would match up.

𝚷(n) = n!, n ∈ 𝗡

You might be bewildered by the complexity of the maths behind this factorial formula, but don't fret!. As a simple trick, we can tell you that (-0.5)! = √π and (0.5)! = 0.5√π.

Interestingly, the first factorial formula is still valid here. So, for example:

(2.5)! = 2.5 × (1.5)! = 2.5 × 1.5 × (0.5)! = 1.875√π

We have already discussed that the factorial is commonly used in probabilistic calculations or permutations, but there is more. Let's see the other places in which the n-factorial appears. Keeping within the realm of pure maths, we arrive at the binomial distribution that helps calculate probabilities of, for example, independent experiments having similar results.

Besides maths, the n-factorial appears in many other calculations, most notably in statistical physics and particle physics, which are parts of physics that deal with the permutations of particles, amongst other things. In particular, statistical physics is a beneficial area of physics that can be thought of as a "microscopic" version of thermodynamics. That is because statistical physics deals with thermodynamics problems (like the one in the latent heat calculator), but it does it from a particle-by-particle basis.

There are other areas (mostly in physics) that use factorials in calculations, and we could dive very deep into how and why they use the factorial formula in their calculations. Still, for a simple calculator like this one, that would be well beyond its reach.

In our modern world, the tedious calculations are generally left to computers (just like you're doing by using this factorial calculator). The usage of coding languages to create small programs that will make those calculations for us are increasingly common. The n-factorial is a perfect candidate since it's not really complex conceptually. It does, however, require too much time for humans to calculate for vast numbers. For those who are using programming languages, we will leave some examples for some of the most common coding languages.

• Python factorial (after 2.6): Use math.factorial(x) to get the Python factorial values.

• Java factorial: There is no 'Java factorial' method in the standard Java packages.

• Factorial Matlab: To calculate a factorial, matlab uses factorial(x). More information on the factorial Matlab function can be found in the official documentation.

• Factorial in Excel: Use FACT to calculate the factorial in excel. Note that the factorial in excel only works with integers.

• Factorial C++: There is no factorial c++ function included in the standard libraries. See here an example of a factorial c++ function.

• Factorial Javascript: There is no factorial javascript function included in the standard libraries.