Prime Factorization Calculator
The prime factorization calculator will take any number and find its prime factors. Simply type the number into our tool and in no time you'll find the prime factorization. To understand the whole process, first you must get familiar with what is a prime factor. Once you understand that, we will move on to the difference between prime factor and prime factorization.
Below, you'll find all the answers, as well as concise information about how to find prime factorization and what a factor tree is.
What is a prime number?
To understand prime factorization, we need to start from the beginning — what is a prime number? A prime number is a number whose only factors are one and itself - in other words, it can't be formed by multiplying two smaller natural numbers. A key point to note is that the two factors must be different, so 1 is not a prime number since both factors of 1 are the same. For example, 5 is a prime number since the only factors of 5 are 1 and 5. 6 is not a prime as, apart from 1 and 6, other factors exist — 2 and 3.
There are infinitely many primes, and there's no simple formula to determine whether a number is a prime or not. That's why this prime factorization calculator is such a great, multi-purpose tool — you can use it as a prime number calculator as well!
What is a prime factor?
Prime factors are factors of a number that are themselves prime numbers. For example, suppose we want to find the factors of 20, that is, we want to know what whole numbers multiply to give you 20. We know that 1 × 20 = 20, 2 × 10 = 20 and 4 × 5 = 20. But notice that 20, 10 and 4 are not prime factors. The only prime factors of 20 are 2 and 5.
What is prime factorization?
Prime factorization is when we break a number down into factors that are only prime numbers. If we look at the above example with 20, the factors are 1, 2, 4, 5, 10, 20. The best place to start is to find at least one initial factor that is prime. Since 5 is prime, we can start with 4 × 5. Notice that 4 is not prime, so we break 4 down into 2 × 2. Since 2 is prime, the prime factorization of 20 is 2 × 2 × 5. Go ahead and check this result with our prime factorization calculator.
How to find prime factorization? A factor tree method
We'll show you step by step how to find prime factorization. We'll use the factor tree diagram, an easy way to break down a number into its prime factors. Are you ready?
- Take a number. There's no point in picking a prime number, as the prime factorization will finish at this point. Let's choose
36. - Factor it into any two numbers, prime or not. You may want to take the easiest splits, e.g., if your number is even, split it into 2 and the other number. 36 is even so that we can write it as
2 * 18. - Start constructing the factor tree. Draw two branches splitting down from your original number.

- Factor the next line. If your number is a prime, leave it as it is. If it's not a prime number, repeat step 2.
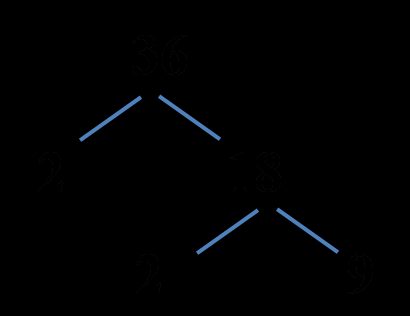
- Repeat step 4 until you're left with only prime numbers.

- Write down the final prime factorization and prime factors.
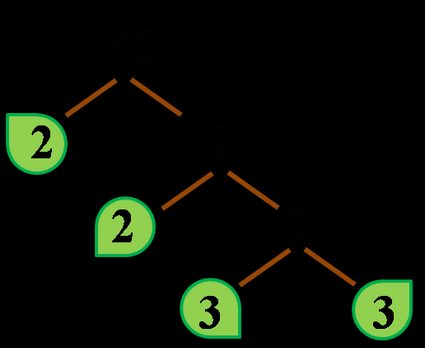
Take all the "leaves" of your factor tree and multiply them together:
36 = 2 × 2 × 3 × 3
That's how we find prime factorization!
The prime factors of our original number 36 are 2 and 3. The same prime factor may occur more than once, which is precisely what happened in our case - both prime numbers appear twice in the prime factorization. We can then express it as:
36 = 2² × 3²
Of course, you should get the same result with a different factor tree splits, as e.g. here:
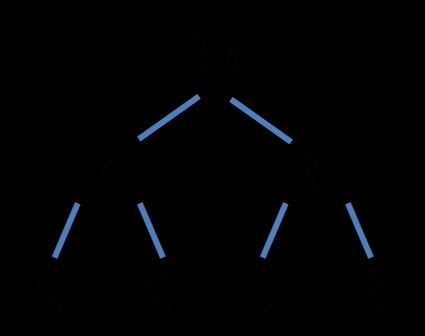
Greatest Common Factor
Prime factorization is the first step in finding the greatest common factor — the greatest factor of two or more numbers. The GCF is especially useful for simplifying fractions and solving equations using polynomials. For example, the greatest common factor between 6 and 20 is 2: prime factorization of the first number is 6 = 2 × 3, the latter may be expressed as 20 = 5 × 2 × 2, and the only number that appears in both prime factorizations is 2, indeed. If you want to calculate the greatest common factor in a snap, use our greatest common factor calculator.
Least common multiple
The prime factorization calculator is also useful in finding the least common multiple (LCM). The LCM is important when adding fractions with different denominators. The least common multiple is obtained when you multiply the higher powers of all factors between the two numbers. For example, the least common multiple between 6 and 20 is (2 × 2 × 3 × 5) = 60. The LCM may be found by hand or with the use of the least common multiple calculator.
What is prime factorization of...
Here is a list of prime factorizations for ease of reference. You can verify these with our prime factorization calculator.
-
2 is prime
-
3 is prime
-
4 = 2 × 2
-
5 is prime
-
6 = 2 × 3
-
7 is prime
-
8 = 2 × 2 × 2
-
9 = 3 × 3
-
10 = 2 × 5
-
11 is prime
-
12 = 2 × 2 × 3
-
13 is prime
-
14 = 2 × 7
-
15 = 3 × 5
-
16 = 2 × 2 × 2 × 2
-
17 is prime
-
18 = 2 × 3 × 3
-
19 is prime
-
20 = 2 × 2 × 5
-
21 = 3 × 7
-
22 = 2 × 11
-
23 is prime
-
24 = 2 × 2 × 2 × 3
-
25 = 5 × 5
-
26 = 2 × 13
-
27 = 3 × 3 × 3
-
28 = 2 × 2 × 7
-
29 is prime
-
30 = 2 × 3 × 5
-
31 is prime
-
32 = 2 × 2 × 2 × 2 × 2
-
33 = 3 × 11
-
34 = 2 × 17
-
35 = 5 × 7
-
36 = 2 × 2 × 3 × 3
-
37 is prime
-
38 = 2 × 19
-
39 = 3 × 13
-
40 = 2 × 2 × 2 × 5
-
41 is prime
-
42 = 2 × 3 × 7
-
43 is prime
-
44 = 2 × 2 × 11
-
45 = 3 × 3 × 5
-
46 = 2 × 23
-
47 is prime
-
48 = 2 × 2 × 2 × 2 × 3
-
49 = 7 × 7
-
50 = 2 × 5 × 5
-
51 = 3 × 17
-
52 = 2 × 2 × 13
-
53 is prime
-
54 = 2 × 3 × 3 × 3
-
55 = 5 × 11
-
56 = 2 × 2 × 2 × 7
-
57 = 3 × 19
-
58 = 2 × 29
-
59 is prime
-
60 = 2 × 2 × 3 × 5
-
61 is prime
-
62 = 2 × 31
-
63 = 3 × 3 × 7
-
64 = 2 × 2 × 2 × 2 × 2 × 2
-
65 = 5 × 13
-
66 = 2 × 3 × 11
-
67 is prime
-
68 = 2 × 2 × 17
-
69 = 3 × 23
-
70 = 2 × 5 × 7
-
71 is prime
-
72 = 2 × 2 × 2 × 3 × 3
-
73 is prime
-
74 = 2 × 37
-
75 = 3 × 5 × 5
-
76 = 2 × 2 × 19
-
77 = 7 × 11
-
78 = 2 × 3 × 13
-
79 is prime
-
80 = 2 × 2 × 2 × 2 × 5
-
81 = 3 × 3 × 3 × 3
-
82 = 2 × 41
-
83 is prime
-
84 = 2 × 2 × 3 × 7
-
85 = 5 × 17
-
86 = 2 × 43
-
87 = 3 × 29
-
88 = 2 × 2 × 2 × 11
-
89 is prime
-
90 = 2 × 3 × 3 × 5
-
91 = 7 × 13
-
92 = 2 × 2 × 23
-
93 = 3 × 31
-
94 = 2 × 47
-
95 = 5 × 19
-
96 = 2 × 2 × 2 × 2 × 2 × 3
-
97 is prime
-
98 = 2 × 7 × 7
-
99 = 3 × 3 × 11
-
100 = 2 × 2 × 5 × 5
-
101 is prime
-
102 = 2 × 3 × 17
-
103 is prime
-
104 = 2 × 2 × 2 × 13
-
105 = 3 × 5 × 7
-
108 = 2 × 2 × 3 × 3 × 3
-
117 = 3 × 3 × 13
-
120 = 2 × 2 × 2 × 3 × 5
-
121 = 11 × 11
-
125 = 5 × 5 × 5
-
126 = 2 × 3 × 3 × 7
-
130 = 2 × 5 × 13
-
132 = 2 × 2 × 3 × 11
-
135 = 3 × 3 × 3 × 5
-
140 = 2 × 2 × 5 × 7
-
144 = 2 × 2 × 2 × 2 × 3 × 3
-
147 = 3 × 7 × 7
-
150 = 2 × 3 × 5 × 5
-
162 = 2 × 3 × 3 × 3 × 3
-
175 = 5 × 5 × 7
-
180 = 2 × 2 × 3 × 3 × 5
-
196 = 2 × 2 × 7 × 7
-
200 = 2 × 2 × 2 × 5 × 5
-
210 = 2 × 3 × 5 × 7
-
216 = 2 × 2 × 2 × 3 × 3 × 3
-
225 = 3 × 3 × 5 × 5
-
245 = 5 × 7 × 7
-
250 = 2 × 5 × 5 × 5
-
256 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2
-
300 = 2 × 2 × 3 × 5 × 5
-
375 = 3 × 5 × 5 × 5
-
400 = 2 × 2 × 2 × 2 × 5 × 5
-
500 = 2 × 2 × 5 × 5 × 5
-
625 = 5 × 5 × 5 × 5
At the beginning, 1 was considered a prime number. It was not until the early 20th century that most mathematicians excluded 1 as a prime number. Notice the prime factorization calculator does not include 1 in the results of prime numbers.