Factor Calculator

With this factor calculator, you will determine the factors of any positive natural number. A factor is any number that divides evenly into another number.

Just enter any positive integer, and in the blink of an eye, you'll find all positive factors of that number. If you are not sure what a factor is, scroll down to see the definition of a factor, as well as divisibility rules with a dedicated paragraph for the not-so-well-known divisibility rule of 7.

A factor, also called a divisor, is any number that divides evenly into another number. In other words, factors are the numbers we can multiply together to get a certain product:

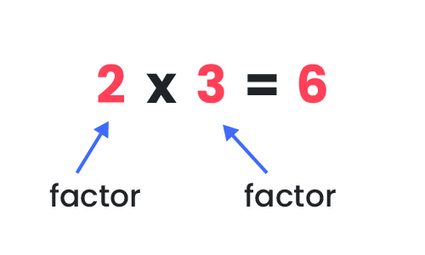
You can also notice that dividing the product by its factor leaves no remainder.

Definition of the factor differs: some definitions claim that factor can be negative as well as positive, but in other cases, the term is restricted to positive factors only.
For example, the factors of 8 are 1, 2, 4, and 8. But, on the other hand, if you multiply -2 times -4, you'll also obtain 8; therefore, -2 and -4 are factors of 8 according to the first definition.

Technically, you can have negative factors, although it's not so popular to use them. For practical purposes, our factor calculator provides only positive factors. If you need negative ones for some reason, just add the minus in front of every obtained value:

Factors of 8 are: 1, 2, 4, 8

plus -1, -2, -4, -8 as well. Feel free to check this result with our factor calculator.

Factors have many applications besides algebra. They are relevant to simplifying and working with fractions, as well as finding patterns in numbers or sequences. Moreover, the process of determining the factors of large prime numbers is computationally hard and is used as a basis for encryption schemes, such as RSA (Rivest–Shamir—Adleman).

There are many rules of divisibility that greatly assist one in finding factors by hand. The most often used ones are:

• 2: Any even number is divisible by 2.

• 3: A number is divisible by 3 if the sum of the digits in the number is divisible by 3.

• 4: A number is divisible by 4 if the last two digits form a number that is divisible by 4.

• 5: Any number ending in 5 or 0 is divisible by 5.

• 6: A number is divisible by 6 if it is divisible by 2 and 3.

• 7: The divisibility rule of 7 also exists, but it's a bit more complicated. Find a short paragraph below.

• 8: If the last three digits form a number that is divisible by 8, then the entire number is divisible by 8.

• 9: If the sum of the digits is divisible by 9, the entire number is divisible by 9.

• 10: Any number ending in 0 is divisible by 10.

There are many aspects of mathematics where it's important to be able to find the factors. The factor calculator helps find the greatest common factor, least common multiple, and prime factorization.

Like many algorithms, our factor calculator has some limitations in factorizing large prime numbers. This is, in fact, a computation challenge since some prime numbers, such as RSA-250, took months to factorize, using 2700 core years of running powerful computer machines. However, we are pretty sure that our tool can easily deal with your factorization challenges.

Want to check if 7 is a factor of our number? There are two basic methods for testing that. Let's show it on the example of the number 13,468.

1. Method 1
   1. Take the last digit. It's 8 in our case.
   2. Double the last digit. 2 × 8 = 16.
   3. Take the remaining digits (truncated number). For us - 1346.
   4. Find the difference between the number from the remaining digits and doubled last digit. This means we need to subtract 16 from 1346. 1346 - 16 = 1330.
   5. Continue to do this procedure until a number known to be divisible by 7 (or not) is obtained. We don't know straight away if 1330 is divisible by 7, so we repeat the steps all over again:

   • 0;

   • 2 × 0 = 0;

   • 133;

   • 133 - 0 = 133.

     Is 133 divisible by 7? Not sure, so repeat the procedure once more:

   • 3;

   • 2 × 3 = 6;

   • 13;

   • 13 - 6 = 7.

Great! We obtained the number divisible by 7, so it means that our original number, 13,468 is also divisible by 7.

2. Method 2

   1. Take the digits of the number in reverse order. So for our original number 13468, we have 8 6 4 3 1.

   2. Multiply them successively by the digits 1, 3, 2, 6, 4, 5. Repeat or shorten this sequence to the necessary length. So in our case, we get:

      8 × 1, 6 × 3, 4 × 2, 3 × 6, and 1 × 4.

   3. Add the obtained products. If the result is divisible by 7, then the original number is also. So:

      (8 × 1) + (6 × 3) + (4 × 2) + (3 × 6) + (1 × 4) = 8 + 18 + 8 + 18 + 4 = 56, which is a number divisible by 7.

Prime factorization is an extension of factorization in which all the factors are prime numbers. For example, suppose we want the prime factorization of 48. The factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 48. Notice that those are not all prime numbers, so we must break them down further. When completing the process, we get 2 × 2 × 2 × 2 × 3. Although 1 is a factor, many mathematicians now do not consider 1 a prime number. The prime factorization calculator is a handy tool for obtaining these factors.

Another area of interest is calculating the greatest common factor (GCF) of a set of numbers. To do so, we get the prime factorization of all the numbers. Then multiply all the factors that are the same in each set. For example, suppose we want the GCF of 24, 44, and 68. The prime factorizations are 24 = 2 × 2 × 2 × 3, 44 = 2 × 2 × 11 and 68 = 2 × 2 × 17. Notice that the only number present in all sets of factors is 2, which appears in common twice, so the GCF is 2 × 2 = 4. The GCF calculator will provide this result simply and quickly.

Closely related to the GCF is the least common multiple, abbreviated as LCM. The process is as follows: we get the prime factorizations and multiply the highest power of all factors present. In the example above, the LCM would be 2 × 2 × 2 × 3 × 11 × 17 = 4,488. The use of the least common multiple calculator will make a sometimes tedious process much easier.

While learning arithmetic, check out our distributive property calculator to learn how to handle complex mathematical expressions.

Finding common factors is especially relevant in factorization, as you can use it to simplify fractions, solve equations, and easily factorize polynomials. Let us see a simple example about removing common factors. Given the numbers $18$ and $24$, we can factorize them as

$18 = 2 \cdot 3 \cdot 3$ and $24 = 2 \cdot 2 \cdot 2 \cdot 3$

then, the fraction $18/24$ can be rewritten as:

$\frac{18}{24} = \frac{2 \, \cdot \, 3^2}{2^3 \, \cdot \, 3} = \frac{3}{4}$.

The same process can be applied to polynomial equations. For instance:

Here, we can see that the common factor $2x^2$ was used to simplify the polynomial equation and allowed us to find the solution $x=3$.

You can use the factor calculator to obtain the list of factors below:

• Factors of 1: 1;

• Factors of 2: 1, 2;

• Factors of 3: 1, 3;

• Factors of 4: 1, 2, 4;

• Factors of 5: 1, 5;

• Factors of 6: 1, 2, 3, 6;

• Factors of 7: 1, 7;

• Factors of 8: 1, 2, 4, 8;

• Factors of 9: 1, 3, 9;

• Factors of 10: 1, 2, 5, 10;

• Factors of 11: 1, 11;

• Factors of 12: 1, 2, 3, 4, 6, 12;

• Factors of 13: 1, 13;

• Factors of 14: 1, 2, 7, 14;

• Factors of 15: 1, 3, 5, 15;

• Factors of 16: 1, 2, 4, 8, 16;

• Factors of 17: 1, 17;

• Factors of 18: 1, 2, 3, 6, 9, 18;

• Factors of 19: 1, 19;

• Factors of 20: 1, 2, 4, 5, 10, 20;

• Factors of 21: 1, 3, 7, 21;

• Factors of 22: 1, 2, 11, 22;

• Factors of 23: 1, 23;

• Factors of 24: 1, 2, 3, 4, 6, 8, 12, 24;

• Factors of 25: 1, 5, 25;

• Factors of 26: 1, 2, 13, 26;

• Factors of 27: 1, 3, 9, 27;

• Factors of 28: 1, 2, 4, 7, 14, 28;

• Factors of 29: 1, 29;

• Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30;

• Factors of 31: 1, 31;

• Factors of 32: 1, 2, 4, 8, 16, 32;

• Factors of 33: 1, 3, 11, 33;

• Factors of 34: 1, 2, 17, 34;

• Factors of 35: 1, 5, 7, 35;

• Factors of 36: 1, 2, 3, 4, 6, 9, 12, 18, 36;

• Factors of 37: 1, 37;

• Factors of 38: 1, 2, 19, 38;

• Factors of 39: 1, 3, 13, 39;

• Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40;

• Factors of 41: 1, 41;

• Factors of 42: 1, 2, 3, 6, 7, 14, 21, 42;

• Factors of 43: 1, 43;

• Factors of 44: 1, 2, 4, 11, 22, 44;

• Factors of 45: 1, 3, 5, 9, 15, 45;

• Factors of 46: 1, 2, 23, 46;

• Factors of 47: 1, 47;

• Factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48;

• Factors of 49: 1, 7, 49;

• Factors of 50: 1, 2, 5, 10, 25, 50;

• Factors of 51: 1, 3, 17, 51;

• Factors of 52: 1, 2, 4, 13, 26, 52;

• Factors of 53: 1, 53;

• Factors of 54: 1, 2, 3, 6, 9, 18, 27, 54;

• Factors of 55: 1, 5, 11, 55;

• Factors of 56: 1, 2, 4, 7, 8, 14, 28, 56;

• Factors of 57: 1, 3, 19, 57;

• Factors of 58: 1, 2, 29, 58;

• Factors of 59: 1, 59;

• Factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60;

• Factors of 61: 1, 61;

• Factors of 62: 1, 2, 31, 62;

• Factors of 63: 1, 3, 7, 9, 21, 63;

• Factors of 64: 1, 2, 4, 8, 16, 32, 64;

• Factors of 65: 1, 5, 13, 65;

• Factors of 66: 1, 2, 3, 6, 11, 22, 33, 66;

• Factors of 67: 1, 67;

• Factors of 68: 1, 2, 4, 17, 34, 68;

• Factors of 69: 1, 3, 23, 69;

• Factors of 70: 1, 2, 5, 7, 10, 14, 35, 70;

• Factors of 71: 1, 71;

• Factors of 72: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72;

• Factors of 73: 1, 73;

• Factors of 74: 1, 2, 37, 74;

• Factors of 75: 1, 3, 5, 15, 25, 75;

• Factors of 76: 1, 2, 4, 19, 38, 76;

• Factors of 77: 1, 7, 11, 77;

• Factors of 78: 1, 2, 3, 6, 13, 26, 39, 78;

• Factors of 79: 1, 79;

• Factors of 80: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80;

• Factors of 81: 1, 3, 9, 27, 81;

• Factors of 82: 1, 2, 41, 82;

• Factors of 83: 1, 83;

• Factors of 84: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84;

• Factors of 85: 1, 5, 17, 85;

• Factors of 86: 1, 2, 43, 86;

• Factors of 87: 1, 3, 29, 87;

• Factors of 88: 1, 2, 4, 8, 11, 22, 44, 88;

• Factors of 89: 1, 89;

• Factors of 90: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90;

• Factors of 91: 1, 7, 13, 91;

• Factors of 92: 1, 2, 4, 23, 46, 92;

• Factors of 93: 1, 3, 31, 93;

• Factors of 94: 1, 2, 47, 94;

• Factors of 95: 1, 5, 19, 95;

• Factors of 96: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96;

• Factors of 97: 1, 97;

• Factors of 98: 1, 2, 7, 14, 49, 98;

• Factors of 99: 1, 3, 9, 11, 33, 99;

• Factors of 100: 1, 2, 4, 5, 10, 20, 25, 50, 100;

• Factors of 104: 1, 2, 4, 8, 13, 26, 52, 104;

• Factors of 105: 1, 3, 5, 7, 15, 21, 35, 105;

• Factors of 108: 1, 2, 3, 4, 6, 9, 12, 18, 27, 36, 54, 108;

• Factors of 110: 1, 2, 5, 10, 11, 22, 55, 110;

• Factors of 112: 1, 2, 4, 7, 8, 14, 16, 28, 56, 112;

• Factors of 117: 1, 3, 9, 13, 39, 117;

• Factors of 120: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60, 120;

• Factors of 121: 1, 11, 121;

• Factors of 125: 1, 5, 25, 125;

• Factors of 126: 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63, 126;

• Factors of 130: 1, 2, 5, 10, 13, 26, 65, 130;

• Factors of 132: 1, 2, 3, 4, 6, 11, 12, 22, 33, 44, 66, 132;

• Factors of 135: 1, 3, 5, 9, 15, 27, 45, 135;

• Factors of 140: 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, 140;

• Factors of 144: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, 144;

• Factors of 147: 1, 3, 7, 21, 49, 147;

• Factors of 150: 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150;

• Factors of 162: 1, 2, 3, 6, 9, 18, 27, 54, 81, 162;

• Factors of 169: 1, 13, 169;

• Factors of 175: 1, 5, 7, 25, 35, 175;

• Factors of 180: 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, 180;

• Factors of 189: 1, 3, 7, 9, 21, 27, 63, 189;

• Factors of 192: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 64, 96, 192;

• Factors of 196: 1, 2, 4, 7, 14, 28, 49, 98, 196;

• Factors of 200: 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 200;

• Factors of 210: 1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70, 105, 210;

• Factors of 216: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 108, 216;

• Factors of 225: 1, 3, 5, 9, 15, 25, 45, 75, 225;

• Factors of 240: 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 20, 24, 30, 40, 48, 60, 80, 120, 240;

• Factors of 245: 1, 5, 7, 35, 49, 245;

• Factors of 250: 1, 2, 5, 10, 25, 50, 125, 250;

• Factors of 256: 1, 2, 4, 8, 16, 32, 64, 128, 256;

• Factors of 270: 1, 2, 3, 5, 6, 9, 10, 15, 18, 27, 30, 45, 54, 90, 135, 270;

• Factors of 288: 1, *2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 72, 96, 144, 288;

• Factors of 294: 1, 2, 3, 6, 7, 14, 21, 42, 49, 98, 147, 294;

• Factors of 300: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 25, 30, 50, 60, 75, 100, 150, 300;

• Factors of 343: 1, 7, 49, 343;

• Factors of 360: 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180, 360;

• Factors of 375: 1, 3, 5, 15, 25, 75, 125, 375;

• Factors of 400: 1, 2, 4, 5, 8, 10, 16, 20, 25, 40, 50, 80, 100, 200, 400;

• Factors of 500: 1, 2, 4, 5, 10, 20, 25, 50, 100, 125, 250, 500; and

• Factors of 625: 1, 5, 25, 125, 625.

You can also visualize such factors with the so-called factor tree diagram.