Binomial Coefficient Calculator

Welcome to the binomial coefficient calculator, where you'll get the chance to calculate and learn all about the mysterious n choose k formula. The expression denotes the number of combinations of k elements there are from an n-element set and corresponds to the nCr button on a real-life calculator.

For the answer to the question "What is a binomial?," the meaning of combination, the solution to "4 choose 2," and the comparison of permutation vs. combination, go ahead and scroll down to the sections below!

In mathematics (algebra to be precise), a binomial is a polynomial with two terms (that's where the "bi-" prefix comes from). For example, the expressions x + 1, xy - 2ab, or x³z - 0.5y⁵ are all binomials, but x⁵, a + b - cd, or x² - 4x² are not (the last one does have two terms, but we can simplify that expression to -3x², which has only one).

Now that we know what a binomial is, let's take a closer look at taking an exponent of one:

(x² - 3)³.

There are some special cases of that expression - the short multiplication formulas you may know from school:

(a + b)² = a² + 2ab + b²,

(a - b)² = a² - 2ab + b².

The polynomial that we get on the right-hand side is called the binomial expansion of what we had in the brackets. Believe it or not, we can find their formulas for any positive integer power. In full generality, the binomial theorem tells us what this expansion looks like:

where:

• $C_k$ is the number of all possible combinations of $k$ elements from an $n$-element set.

Also, for a given n, these numbers are neatly presented for consecutive values of n in the rows of the so-called Pascal's triangle, where a single row as whole counts all possible subsets of the set (i.e., the cardinality of the power set). Visit our Pascal's triangle calculator to generate Pascal's triangle of your chosen size.

And this marks a good moment for us to check out the meaning of "combination" – as we've mentioned so many times already.

Imagine that you're a college student, taking a casual nap during a lecture. Suddenly, the teacher brings you back to earth by saying, "Let's choose the groups for the mid-term projects at random." Well, it looks like you'll have to do some work, after all.

The problem is that there's only one guy that you'd like to work with on the project. If there are twenty people in the group, and the teacher divides you into groups of four, how probable is it that you'll be with your friend?

Every possible group is an example of a combination. In this case, a combination of four elements from a twenty-element set, or, if you prefer, of four students from a twenty-person group. If you'd like to get a bit technical, choosing a combination means picking a subset of a larger set. What is most important here is that the order of the elements we choose doesn't matter. After all, all members of a project team are equal (except those that don't do any work).

The number of combinations of k elements from a set of n elements is denoted by

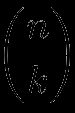
(like a fraction of n divided by k but without the line in between) which we read as "n choose k." This is also the symbol that appears when we choose push nCr on a calculator (not our binomial coefficient calculator, but a regular, real-life one). For example,

is "4 choose 2" and

is "6 choose 2." In some textbooks, the binomial coefficient is also denoted by C(n,k), making it a function of n and k. "And how do I calculate it?" Well, easily enough. The n choose k formula is

n! / (k! × (n - k)!).

The exclamation mark is called a factorial. The expression n! is the product of the first n natural numbers, i.e.,

n! = 1 × 2 × 3 × ... × n.

This means that, for example, the 4 choose 2 from above is

4! / (2! × (4 - 2)!) = (1 × 2 × 3 × 4) / (1 × 2 × 1 × 2) = 6,

and 6 choose 2 is

6! / (2! × (6 - 2)!) = (1 × 2 × 3 × 4 × 5 × 6) / (1 × 2 × 1 × 2 × 3 × 4) = 15.

For more on factorials, visit our factorial calculator!

So we can choose two elements from a set of four in six different ways and from a set of six in fifteen ways.

Before we move on, let's take one more look at the n choose k formula. We can get from it a quite interesting symmetric property.

If we take n choose n - k, then we'll get

n! / ((n - k)! × (n - (n - k))!) = n! / ((n - k)! × k!)

which is the same as n choose k (since multiplication is commutative). In other words, we have

or C(n,k) = C(n,n-k) in the other notation.

In the section above, we've seen what a factorial is. In combinatorics, it denotes the number of permutations. A permutation of length n means putting n elements in some order. For example, if we have three cute kitten expressions, say 😹, 😻, and 🙀, then we can order them in six different ways:

(😹, 😻, 🙀)

(😹, 🙀, 😻)

(😻, 😹, 🙀)

(😻, 🙀, 😹)

(🙀, 😹, 😻)

(🙀, 😻, 😹).

Observe that this agrees with what the factorial tells us:

3! = 3 × 2 × 1 = 6.

Visit our permutation calculator for a deeper dive.

Note that we can also understand this formula like this: we choose the first element out of three (3 options), the second out of the two remaining (because we've already chosen one – 2 options), and the third out of the one that's left (because we've already chosen two – 1 option). We multiply the number of choices: 3 × 2 × 1 = 6, and get the factorial.

When we compare permutation vs. combination, the keyword is order. As we've said in the previous section, the meaning behind a combination is picking a few elements from a bigger collection. In essence, we say which ones we pick, but not which is first, second, etc. They form a set as a whole.

A permutation, however, puts the elements in a fixed order, one after the other, making it a sequence rather than a set. Moreover, a permutation uses all elements from the set we've had, while a combination only chooses some of them.

As an example, once again, put yourself in the college student's shoes. When the teacher chose the group for you, they picked a combination. And when it comes time to present your project, and they ask one question to each of you, they choose a permutation (determining the order in which they ask you the questions). And we all know how important the order can be for your final grade.

Binomial coefficients are one of the most important number sequences in discrete mathematics and combinatorics. They appear very often in statistics and probability calculations, and are perhaps most important in the binomial distribution (including the negative binomial distribution). Does that mean that only geeky mathematicians have any real use for it?

Not at all! Every gambling game is based on chance, and binomial coefficients are the vital player. A simple coin toss is the easiest example, which you can calculate with our coin flip probability calculator. However, let's go one step further and look at poker.

Have you ever wondered why some hands in poker are more valuable than others? That's simply because they are rarer (unless someone's cheating, but we've seen enough gangster TV series to know that it's usually a bad idea).

There are 52 cards in a regular deck, and in Texas hold 'em, a player gets five cards. Our binomial coefficient calculator and the n choose k formula (in our case with n = 52 and k = 5) tells us this translates to 2,598,960 possible hands in a game of poker. Quite a lot, don't you think? And now consider the best possible hand – a royal flush in clubs (Ace, King, Queen, Jack, and 10). This hand can happen only in one case – when we get exactly those cards. This means that it is a 1 in 2,598,960 chance to have it. We wouldn't recommend putting all of your savings on those odds.

Let's take another example – a full house (three of a kind and a pair). This time there are considerably more possibilities. After all, any of the 13 cards in a suit can be the three of a kind, and the pair is in one of the other 12 cards (it cannot be the same value as the triple). Moreover, the three of a kind are in only three of the four card symbols, and similarly, the pair is in only two.

And that's where we recall the meaning of a combination! We need to choose three out of four symbols for the triple and a combination of two out of four for the pair. The n choose k formula translates this into 4 choose 3 and 4 choose 2, and the binomial coefficient calculator counts them to be 4 and 6, respectively. All in all, if we now multiply the numbers we've obtained, we'll find that there are

13 × 12 × 4 × 6 = 3,744

possible hands that give a full house. Well, not too many compared to all the possibilities, but at least it's 3,744 times more probable than the royal flush on clubs.

Still, we suggest regularly saving money as a better investment technique than gambling.