Combination Calculator
This combination calculator (n choose k calculator) is a tool that helps you not only determine the number of combinations in a set (often denoted as nCr), but it also shows you every single possible combination (or permutation) of your set, up to the length of 10 elements (or 300 combinations/permutations). However, be careful! The final result may be very long in our combination generator. If you wonder how many different combinations can be possibly made of a specific number of elements and sample size, try our combination calculator now!
If you're still not sure what a combination is, it will all be explained in the following article. You'll find here a combination definition together with the combination formula (with and without repetitions). We'll show you how to calculate combinations, and what the linear combination and combination probability are. Finally, we will talk about the relation between permutation and combination. Briefly, permutation takes into account the order of the members and combination does not. You can find more information below!
Have you ever wondered what your chances are of winning the main prize in a lottery? How probable is winning the second prize? To answer both and similar questions, you need to use combinations. We've got a special tool dedicated to that kind of problem. Our lottery calculator doesn't only estimate the combination probability of winning any lottery game but also provides a lottery formula. Try it! You'll find out how big (or small) those numbers are, in fact.
What is a combination? - combination definition
The combination definition says that it is the number of ways in which you can choose r elements out of a set containing n distinct objects (that's why such problems are often called "n choose r" problems). The order in which you choose the elements is not essential as opposed to the permutation (you can find an extensive explanation of that problem in the permutation and combination section).
Seeking for every combination of a set of objects is a purely mathematical problem. You probably have already been taught, say, how to find the greatest common factor (GCF) or how to find the least common multiple (LCM). Well, a combination is an entirely different story. Let's see how complicated it might be.
Imagine a bag filled with twelve balls, where each one is a different color. You pick five balls at random. How many distinct sets of balls can you get? Or, in other words, how many different combinations can you get?
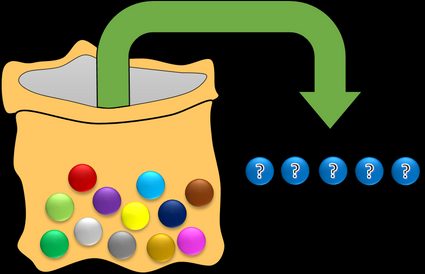
How to calculate combinations? - combination formula
Mathematicians provide the exact solution for many various problems, e.g., how to calculate square footage or how to calculate volume. Is there a similar approach to estimating the number of combinations in the above example with balls?
Luckily, you don't have to write down all of the possible sets! How to calculate the combinations, then? You can use the following combination formula that will allow you to determine the number of combinations in no time:
where:
- is the number of combinations;
- is the total number of elements in the set; and
- is the number of elements you choose from this set.
The exclamation mark represents a factorial. Check out our factorial calculator for more information on this topic. The expression on the right-hand side is also known as the binomial coefficient.
Let's apply this equation to our problem with colorful balls. We need to determine how many different combinations there are:
💡 You can check the result with our nCr calculator. It will list all possible combinations, too! However, we limited the output to 300 combinations, which is already quite a lot to show. If there are too many generated combinations, the combination generator will tell you about it.
You may notice that, according to the combinations formula, the number of combinations for choosing only one element is simply . On the other hand, if you have to select all the elements, there is only one way to do it. Let's check this combination property with our example. You've got the total number of objects that equals . Every letter displayed in the nCr calculator represents a distinct color of a ball, e.g., A is red, B is yellow, C is green, and so on. If you choose only one element at once from that set, the number of combinations will be - because there are 12 different balls. However, if you choose elements, there'll be only possible combination that includes every ball. Try it by yourself with the n choose r calculator!
By this point, you probably know everything you should know about combinations and the combination formula. If you still don't have enough, in the next sections, we write more about the differences between permutation and combination (that are often erroneously considered the same thing), combination probability, and linear combination.
Permutation and combination
Imagine you've got the same bag filled with colorful balls as in the example in the previous section. Again, you pick five balls at random, but this time, the order is important - it does matter whether you pick the red ball as first or third. Let's take a more straightforward example where you choose three balls called R(red), B(blue), G(green). There are six permutations of this set (the order of letters determines the order of the selected balls): RBG, RGB, BRG, BGR, GRB, GBR, and the combination definition says that there is only one combination! This is the crucial difference.
By definition, a permutation is the act of rearrangement of all the members of a set into some sequence or order. However, in literature, we often generalize this concept, and we resign from the requirement of using all the elements in a given set. That's what makes permutation and combination so similar. This meaning of permutation determines the number of ways in which you can choose and arrange r elements out of a set containing n distinct objects. This is called r-permutations of n (sometimes called variations). If you're after an even more in-depth explanation, the permutation calculator should satisfy this need.
The permutation formula is as below:
Doesn't this equation look familiar to the combination formula? In fact, if you know the number of combinations, you can easily calculate the number of permutations:
This combination calculator allows you to find the number of permutations by selecting the corresponding option in the checkbox.
You may wonder when you should use permutation instead of a combination. Well, it depends on whether you need to take order into account or not. For example, let's say that you have a deck of nine cards with digits from 1 to 9. You draw three random cards and line them up on the table, creating a three-digit number, e.g., 425 or 837. How many distinct numbers can you create?
Check the result with our nCr calculator! And how many different combinations are there?
The number of combinations is always smaller than the number of permutations. This time, it is six times smaller (if you multiply 84 by , you'll get 504). It arises from the fact that every three cards you choose can be rearranged in six different ways, just like in the previous example with three color balls.

Permutation and combination with repetition. Combination generator
To complete our considerations about permutation and combination, we have to introduce a similar selection, but this time with allowed repetitions. It means that every time after you pick an element from the set of n distinct objects, you put it back to that set. In the example with the colorful balls, you take one ball from the bag, remember which one you drew, and put it back to the bag. Analogically, in the second example with cards, you select one card, write down the number on that card, and put it back to the deck. In that way, you can have, e.g., two red balls in your combination or 228 as your permutation.
You probably guess that both formulas will get much complicated. Still, it's not as sophisticated as calculating the alcohol content of your homebrew beer. In fact, in the case of permutation, the equation gets even more straightforward. The formula for combination with repetition is as follows:
and for permutation with repetition:
In the picture below, we present a summary of the differences between four types of selection of an object: combination, combination with repetition, permutation, and permutation with repetition. It's an example in which you have four balls of various colors, and you choose three of them. In the case of selections with repetition, you can pick one of the balls several times. If you want to try with the permutations, be careful, there'll be thousands of different sets! However, you can still safely calculate how many of them are there (permutations are available in our tool).
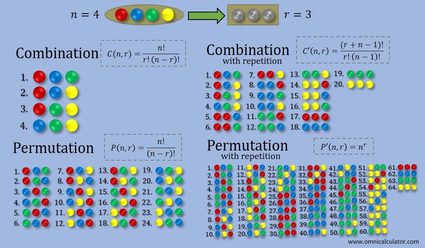
Combination probability and linear combination
Let's start with the combination probability, an essential in many statistical problems. An example pictured above should explain it easily - you pick three out of four colorful balls from the bag. Let's say you want to know the chances (probability) that there'll be a red ball among them. There are four different combinations, and the red ball is in the three of them. The combination probability is then:
If you draw three random balls from the bag, in 75% of cases, you'll pick a red ball. To express probability, we usually use the percent sign.
Now, let's suppose that you pick one ball, write down which color you got, and put it back in the bag. What's the combination probability that you'll get at least one red ball? This is a 'combination with repetition' problem. From the picture above, you can see that there are twenty combinations in total and red ball is in ten of them, so:
Is that a surprise for you? Well, it shouldn't be. When you return the first ball, e.g., blue ball, you can draw it as a second and third ball too. The chances of getting a red ball are thus lowered. You can do analogical considerations with permutation. Try to solve a problem with the bag of colorful balls: what is the probability that your first picked ball is red?
Let's say you don't trust us, and you want to test it yourself. You draw three balls out of four, and you check whether there is a red ball or not (like in the first example of this section). You repeat that process three more times, and you get the red ball only in one of four cases - of cases. You expected according to theory. What happened? Well, this is how probability works! There is the law of large numbers that describes the result of performing the same experiment a large number of times. If you repeat drawing, e.g., one hundred times, you'll be much closer to .
What's more, the law of large numbers almost always leads to the standard normal distribution, which can describe, for example, intelligence or the height of people, with a so-called p-value. Keen to learn more? Normal distribution calculator is the place to go!
Have you ever heard about the linear combination? In fact, despite it have the word combination, it doesn't have much in common with what we have learned so far. Nevertheless, we'll try to explain it briefly. A linear combination is the result of taking a set of terms and multiplying each term by a constant and adding the results. It is frequently used in wave physics to predict diffraction grating equation or even in quantum physics because of the de Broglie equation. Here, you can see some common examples of linear combination:
- Vectors. Every vector in 3D can be decomposed into three unit vectors , and . For example, and that's linear combination.
- Functions. Let's say you've got two functions and . From those two functions you can create linear combinations that describe the hyperbolic sine or cosine . You can do a similar thing with the normal sine and cosine, but you need to use the imaginary number . We write about it more in the last section of the square root calculator.
- Polynomials. For example, you've got three polynomials , , and you want to express the function as a linear combination of those polynomials. It's not always possible to do so, but in this case .
FAQs
What is the difference between permutation and combination?
The fundamental difference between combinations and permutations in math is whether or not we care about the order of items:
- In permutation the order matters, so we arrange items in sequential order.
- In combinations the order does not matter, so we select a group of items from a larger collection.
How do I calculate permutations from combinations?
If you already have a combination and want to turn it into a permutation, you need to impose order on the set of items, i.e., choose one of the possible orderings for your set. Hence, the number of permutations of r items chosen from n items is equal to the number of combinations of r items chosen from n items multiplied by the number of orderings of these r items, i.e., by r!.
How do I calculate combinations from permutations?
If you already have a permutation and want to turn it into a combination, you need to remove order, i.e., regard all possible reorderings as the same object. Hence, the number of combinations of r items chosen from n items is equal to the number of permutations of r items chosen from n items divided by the number of orderings of these r items, i.e., by r!.
How many ways can I arrange a 7 letter word?
If the word has seven distinct letters, you have 7! = 5040 ways of arranging them (simple permutations of seven items). However, if some letters appear more than once, the number of arrangements gets reduced! For instance:
- If the word is "WITNESS", we have "S" appearing twice, so we divide
7!by2! = 2and the result is2520. - If the word is "SOMEONE", we have "O" and "E" appearing twice, so we divide
7!by2! ⋅ 2! = 4and the result is1260. - If the word is "UNKNOWN", we have "N" thrice, so we divide
7!by3! = 6and the result is840.