Conic Sections Calculator

An exciting family of curves originates from intersecting a cone with a plane: discover them with our conic sections calculator! Select the conic section you need, insert the parameters, and let the conic equation calculator give you the results.

Conic sections show useful and intriguing properties and are – undeniably – elegantly generated!

Here you will learn:

• What are the conic sections;
• The formulas for conic sections;
• The various types of conic sections;
• How to calculate their eccentricity and other characteristics; and
• Where we use conic sections in real life!

Let's discover more about them.

A cone is a solid figure generated by rotating a tilted line – the generatrix of the cone – around an axis (fun fact, the word "cone" refers to a double cone, and what we use in everyday life should be called "nappe". But "traffic nappe" doesn't sound right, does it?).

Take a double cone – a cone mirrored on its vertex – and imagine cutting it with a plane you can tilt freely.

As the angle of the plane changes, you get a set of varying curves. Going from a horizontal to a vertical plane, we can generate the following types of conic sections:

• Circle when the plane is parallel to the "base" of the cone;
• Ellipse when the angle is arbitrary, between $0$ and the angle of the generator of the cone (excluded);
• Parabola when the plane lies parallel to the generating line of the cone; and
• Hyperbola where the plane is tilted by an angle between the generator and 90 degrees, i.e., when the plane is vertical.

Some people consider the circle an ellipse that lost its way, but we included it in our conic section calculator anyway!

Every conic section has a set of characteristic elements which define it:

• The foci (or focus): one of two points that define the curve thanks to the sum of distances; and
• The directrix (or directrices): lines that define the curve thanks to the ratio of two distances.

One or more parameters appear in the equation: $a$ and $b$. They are usually called axes. Now that we know what we need to draw to get our conic section, we are going to see how those elements vary in a pencil:

• An ellipse is defined by two foci and two directrices. The foci are placed on the major axis, $a$. The sum of the distances of every point of the ellipse from both foci is a constant.

• A circle is a particular ellipse where $a = b$: consequently, the foci coincide, and the directrix is at an infinite distance from the curve.

• A parabola has a single directrix and one focus, with the other one placed at infinity. A given point of a parable is at the same distance from both the focus and the directrix. You can meet this conic at our parabola calculator.

• A hyperbola has two directrices and two foci. The difference in the distance between each point and the two foci is constant (it is the opposite of an ellipse, in a way).

In the table below, you can see the equations of the various conics!

Mathematicians use a set of parameters to identify different conic sections:

• The eccentricity;
• The linear eccentricity;
• The latus rectum; and
• The focal parameter.

Let's take a look at them!

The eccentricity of a conic section, which unfortunately doesn't measure the quirkiness of a curve, gives information of how the curve is... out of the center, the name says it!

The eccentricity $e$ is defined as the ratio between the sines of the angle of the cutting plane ($\beta$) and the angle of the cone generator ($\alpha$):

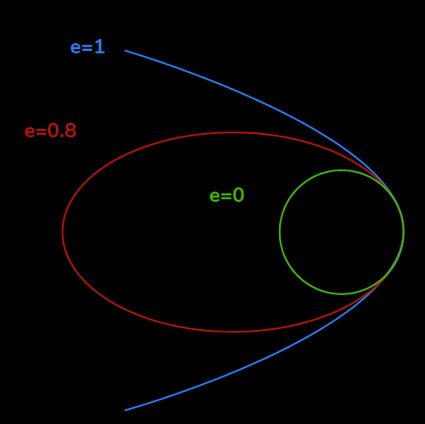
The eccentricity is always defined. Let's take a look at the values that it can assume:

• For a circle, $\beta = 0$, thus $e = 0$: the circle has no eccentricity, and this sounds, somehow, right.

• An ellipse has $0 < \beta < \alpha$, thus the ratio is between $0$ and $1$ (with a shape varying from a barely slanted circle to an ellipse that closes at infinity).

• The parabola has $\beta = \alpha$, implying $e = 1$.

• The hyperbola has $90 > \beta > \alpha$, which translates to an eccentricity bigger than $1$.

The linear eccentricity $c$ is closely related to the concept of eccentricity, but it's not always defined. It equals the distance between the center of the conic section and one of its foci.

The value of the linear eccentricity for a parabola is not defined since it has no center!

The latus rectum (it's just the Latin of "straight side") is the length of the segment parallel to the directrix joining the curve and passing through the corresponding focus. It is usually given in the form of semi-latus rectum $l$, which is half of the value mentioned above.

Last but not least, the focal parameter $p$ measures the distance between the directrix and the corresponding focus. It is always defined, but in the case of a circle, it equals infinity due to the position of the directrix.

Using the conic section calculator is easy, believe us. Just choose the curve you need, and input the value of $a$ and $b$, if required. Nothing more than that.

In the table, you can see how to calculate the eccentricity and all other parameters! The first column contains the conic section equations that define the curves.

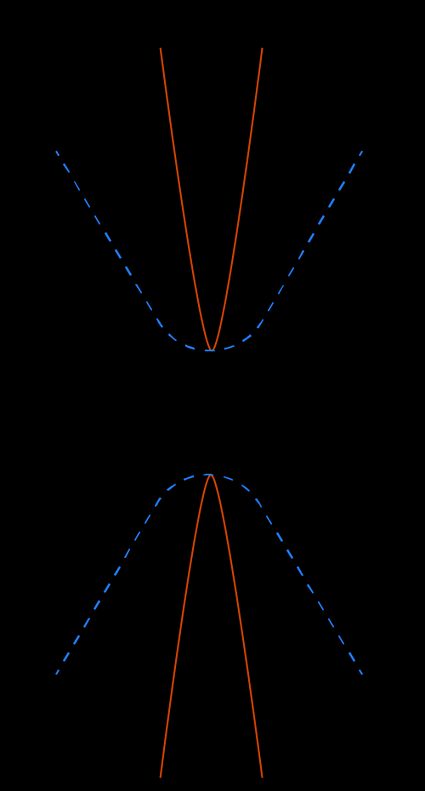
Let's test the conic equation calculator. We will choose a vertical hyperbola because there's nothing better in this world than one of them (this is hyperbole, by the way).

If we choose the value $4$ for $a$, and set $b=0.5$, we would get a really "pointy" hyperbola. Take a look at the values:

Compare the eccentricity of a vertical hyperbola with $a=2$ and $b=20$ (a more "open" one, then): $e = 10.05$. A higher eccentricity is associated with a less circular shape. An infinite eccentricity would see the hyperbola as a straight line parallel to the directrix.

Conic sections, even if at first glance they may look like abstract geometrical constructions, have an essential role on a... bigger scale! Every type of conic section has some application outside of a textbook.

The rules of orbital mechanics, the laws that control the motion of massive bodies under the effect of gravitational forces, are closely tied to the curves we just met. Omni has many tools related to orbital mechanics: try our orbital velocity calculator, for example. 😁

Two bodies orbiting each other (let's say the Moon and the Earth move on elliptical orbits: it's one of the most groundbreaking discoveries in astronomy, thanks to Kepler. However, the eccentricity of Earth's orbit is extremely small, only 0.017!

And to move the Apollo 11 capsule from the Earth to the Moon, scientists calculated an elliptic transfer, all without computers. We are sure they would have liked a tool to calculate conic section equations, too. You can use our Hohmann transfer calculator to discover the maneuver used by the engineers.

Hyperbolas and parabolas are used to describe trajectories of bodies not gravitationally bounded but just passing by.

Keeping our feet on the ground but still looking up, parabolas use the geometric property of reflecting every line hitting it on the inside toward the focus to concentrate the signal from a satellite (reaching the dish in parallel rays) in a single point. It also works in the opposite way, and that's how scientists communicate with deep space probes!