Orbital Velocity Calculator

This orbital velocity calculator is an advanced tool that you can use to find parameters of planet motion in an elliptical orbit (or in a circular orbit). Do you want to learn what the orbital velocity of Earth is or Jupiter's orbital period? With our orbital velocity calculator, you can quickly estimate the following:

• Orbital radius of the planets;
• Orbital energy of the planets;
• Orbital speed of the planets; and
• Orbital period of the planets (see also the orbital period calculator).

You surely know that planets orbit around stars, but have you ever wondered what an elliptical orbit is? As the name suggests, planets do not move around in a circle but in an ellipse. Use our ellipse calculator to learn what an ellipse is and how to estimate all the parameters of an ellipse.

With our elliptical orbit definition, you will be able to find what is Earth's elliptical orbit, including its apoapsis and periapsis distances and Earth's orbital velocity at those points. The apoapsis and periapsis are, respectively, the farthest and the closest points at which the Earth comes to the Sun (in many calculations, we often use just an average orbital radius of Earth). In this certain case, we can call them aphelion and perihelion since Earth orbits around the Sun.

Our orbital velocity calculator makes use of several astrophysical relations. For example, to describe the geometrical properties of Earth's elliptical orbit, you only need to know the semi-major and semi-minor axes or the eccentricity of Earth's orbit. If you want to find more details, like Mars' sidereal period or its satellite speed, you should also enter the masses of the star (e.g., Sun) and the satellite (e.g., Mars, Moon). We can compute it with the Kepler laws and the orbital velocity equation.

Finally, with the so-called vis-viva equation, you can find out what is, for example, the orbital velocity of the Earth.

At the end of this orbital velocity calculator, you can find the planet data table with orbital parameters of different planets of the Solar System.

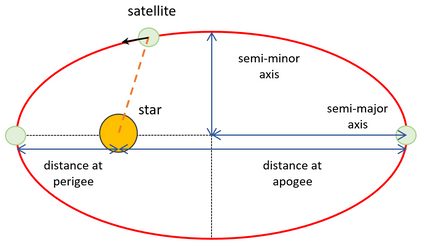
An elliptical orbit (or an elliptic orbit) is a Kepler orbit with an eccentricity between one and zero (an orbit is circular when its eccentricity equals zero). The orbital eccentricity is a parameter that characterizes the shape of the orbit. The higher its value, the more flattened ellipse becomes. It is linked to the other two important parameters: the semi-major axis and semi-minor axis (see figure below), with the following eccentricity formula:

where:

• $e$ – Eccentricity;
• $a$ – Semi-major axis; and
• $b$ – Semi-minor axis.

Knowing the above parameters, we can determine the closest possible distance of the satellite (planet) to a star – periapsis, and the farthest possible distance – apoapsis.

Now that you have learned what an elliptical orbit is, we can estimate distances to a star at periapsis and apoapsis with the following elliptical orbit definition:

where:

• $r_{\rm a}$ – Distance between star and satellite at apoapsis; and
• $r_{\rm p}$ – Distance between star and satellite at periapsis.

The only thing we need to do is to solve the above system of orbit equations. You can, of course, use our orbital velocity calculator to do it!

For example, you can analyze Earth's elliptical orbit. The semi-major axis of Earth's orbit is $a = 1\ \rm au$ (1 au is one astronomical unit which is an average distance between the Earth and the Sun), and the semi-minor axis of Earth's orbit is $b \approx 0.99986\ \rm au$.

Therefore eccentricity $\small e = 0.0167$, distance at aphelion (apoapsis) $\small r_{\rm a} = 1.0167\ \rm au$ and distance at perihelion (periapsis) $\small r_{\rm p} = 0.9833\ \rm au$.

In astrophysics, the vis-viva equation allows us to model the motion of orbiting satellites. It provides the orbital speed of a satellite at a given point of an elliptic orbit as well as an orbital velocity of a satellite in periapsis and apoapsis. The vis-viva equation is as follows:

where:

• $v$ – Relative satellite speed (compared to the speed of a star);
• $\mu$ – Standard gravitational parameter $\small \mu = G(M + m)$;
• $r$ – Distance between the star and the satellite;
• $G$ – Gravitational constant $\small G = 6.674 \times 10^{-11}\ \rm N\! \cdot\! m^2/kg^2$;
• $M$ – Mass of the star; and
• $m$ – Mass of the satellite.

The standard gravitational parameter $\mu$ is expressed in SI units m³/s², but in the scientific literature and spacecraft navigation, we usually use the units of km³/s².

With the above orbital speed formula, you can also estimate the satellite speed at apoapsis $\small (r = r_{\rm a})$ and periapsis $\small (r = r_{\rm p})$. Using the orbital speed calculator, you can compute that the orbital velocity of the Earth at periapsis is $\small v_{\rm p} = 30.29\ \rm km/s$ and at apoapsis is $\small v_{\rm a} = 29.295\ \rm km/s$.

You have learned, from the previous sections, how to use the orbit equation to estimate, e.g., the orbital radius of the Earth. But how can you calculate the orbital period of other planets? The answer derives from the Kepler laws of planetary motion:

1. First law of Kepler – the law of orbits: Every planet of the Solar System moves around the Sun on an elliptical orbit. It is important to remember that the Sun is not at the center but at one of the two foci points of the elliptical orbit.

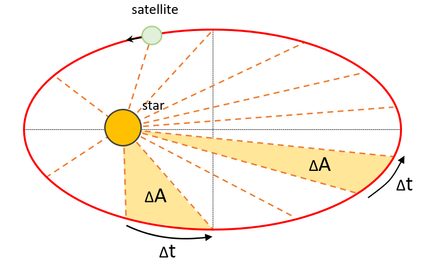
2. Second law of Kepler – the law of areas: At equal intervals, a line segment between a planet and the Sun sweeps out equal areas (area speed is constant).

3. Third law of Kepler – the law of periods: You can obtain the simplified form of the third law of Kepler by comparing the centripetal force to the gravitational force (see gravitational force calculator). The full corresponding formula states that the orbital period of a satellite $T$ is given by:

We encourage you to try our orbital velocity and calculate the orbital period of the Earth ($\small a = 1\ \rm au$). You will see that it equals precisely one year.

You can use our calculator to compute the orbital energy $E$ of planets too. Under standard assumptions, the total orbital energy of planets is negative and independent of the ellipse's eccentricity. We can calculator it with the following orbital energy formula:

You should note that the orbital energy of the Earth (and other planets, too) is large (~ 10³³ J). Check our energy conversion calculator if you want to find out what are other orders of magnitude of energies can be found in nature.

Are you looking for Neptune's orbital period? Or maybe you're interested in Jupiter's orbital speed velocity? If you want to quickly estimate the orbital properties of different planets in the Solar System, you can use our orbital velocity calculator alongside the below planet data table.

With the information from the above planet data table, you can compute every orbital parameter provided by our orbital speed calculator. Try with different planets! Just remember that the distance between a planet and the Sun is expressed in astronomical units (average orbital radius of the Earth), and the mass is in units of Earth's masses.