Orbital Period Calculator

Before the orbital period calculator was available, calculating the orbital period of a binary star system or other planets seemed daunting, not to mention learning Kepler's laws of planetary motion. Now, you don't need to know what is Kepler's third law, elliptical orbits, or orbital period equations; simply put the numbers and get the result.

We will also teach you about the geostationary orbit, low Earth orbit, and geosynchronous orbits, as well as Johannes Kepler and all his contributions to deciphering planet's orbits in our solar system.

When we talk about orbits, it is very clear that we're already in the realm of astronomy and celestial objects. In this context, the meaning of an orbit is clearly defined as the path a body follows in its movement around a different object. For example, Earth's orbit around the Sun is the path that our precious planet traverses around the Sun every year.

But not every planet needs a year, that is, 365 days, to go around the Sun. And this gets even more complicated if we don't look at the Earth's, but for example, at the Moon's orbit. Here is where the concept of orbital period needs to be introduced, and the question "what is the orbital period?" needs to be answered. Luckily for us, the answer is very simple: the orbital period is the time it takes to move completely around the central object, or in other words, the time it takes to go once around the orbit. It is also referred to as the sidereal period: learn how to calculate it with Omni's synodic period calculator.

The only problem now is how to calculate such a period for any two objects orbiting one another. In general, this process is not straightforward and requires you to calculate the gravitational force that one object exerts on the other and solve all the equations. Johannes Kepler did all of this using Newton's approximation and obtained a very simple result. Now, all we have to do is to use that orbital period equation and get the results quickly.

Johannes Kepler was a very famous German astronomer in the 17th century. One of his most significant contributions to astronomy is what we now call the three Kepler's laws of planetary motion. These three laws summarize perfectly how planets revolve around stars and can predict the planet's orbits and orbital periods with an accuracy unheard at the time. He did all of this by using (among other tricks) elliptical orbits instead of the commonly used circular orbits, as you can see in our Kepler's third law calculator!

To get more information on each of Kepler's three laws of planetary motion, we recommend checking out our orbital velocity calculator, where they are explained in detail, especially Kepler's third law. Here we will, nonetheless, explain briefly what each of them means.

The first of Kepler's laws of planetary motion states that the orbits of planets around the Sun are ellipses, with the Sun at one of the foci. This is a big departure from the previous theories that located the Sun in the center of a circumference/sphere that would dictate the movement of the planets. It's interesting to note, though, that if we consider that a circumference is an ellipse with zero eccentricity, Kepler's laws of planetary motion reduce to the old laws about circles and circumferences.

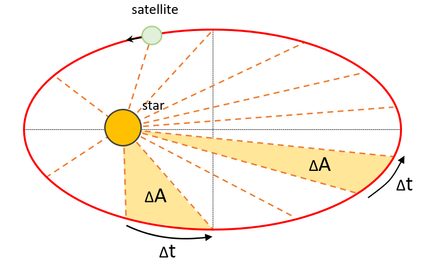
The second of these laws states that for similar periods of time, the area of the ellipse corresponding to the movement of the planet is the same. This is best seen in the picture accompanying the abovementioned orbital velocity calculator. One of the striking implications is that the closer a planet is to the Sun, the faster the speed with which it moves. This is observed not only for the planets but most significantly for comets, and other bodies orbiting the Sun.

Finally, we arrive at Kepler's third law, which is the most practical one since it not only provides the orbital period equation but also tells us how to calculate the orbital period of a planet. Kepler's 3rd law states that the square of the orbital period of a planet is directly proportional to the cube of the semi-major axis of the elliptical orbit it follows around the Sun. The constant of proportionality can be either calculated theoretically or estimated experimentally.

This is the point where we can prove that Kepler's laws of planetary motion (in particular Kepler's third law) are compatible with Newton's law of gravitation.

Kepler's laws describe specifically the movement of planets around the Sun or any other star for that matter. However, with a bit of magic – mathematical skills – we can extend them to any system of two bodies orbiting each other. Two extreme examples of this are low Earth orbit and a binary star system. Let's see how each of these differs from the star-planet system.

First, let's establish what is the low Earth orbit. Low Earth orbit is an orbit located very close to the surface of the Earth, where satellites can move around the Earth without falling into it. This low Earth orbit is so close to the surface of the Earth, compared to the size of the planet, that we can consider the satellite to be orbiting just on its surface. The fact the Earth is (effectively) infinitely more massive than the satellite, allows us to make some approximations. These approximations simplify the equations of motion so much that we can calculate the orbital period with only the mean density of the central mass, in this case, the Earth. We can use the resulting equation with any small body orbiting a massive central body very close to its surface.

Moving on to what is a binary star system, we find pretty much the opposite situation to the low Earth orbit. For those still asking what is a binary star system, we should clarify: a binary star system is such a system where two stars are so close to each other and have such similar masses that both stars orbit each other without a material central body. You could think of this system as a more democratic compared to the master-slave relationship that we find in the solar system, where the Sun effectively stands still while the rest of the planets orbit around it. In the case of the binary star system, we still have elliptical orbits. The difference is that the focus of the ellipse described by each star's orbit is somewhere between the stars. You can pretend that one of them is still (using it as the frame of reference) and calculate the orbital period of the other using simple equations.

But how to calculate the orbital period in these extreme cases, you may ask. Don't fret! We have the perfect tool for your astronomical needs: The orbital period calculator from Omni Calculator. Let's now see how you can use this fantastic tool to calculate orbital periods of binary systems and small satellites without breaking a sweat.

If you turn your attention to the calculator itself, you will see that it has two distinct parts: one labeled "Satellite around central body" and the second one aptly named "Binary system".

For this first part, we will focus on the top part of the calculator, which will help us calculate orbital periods for small satellites orbiting on the low Earth orbit. In this section, we have only two fields to fill, so it will be easy. As we mentioned before, you only need to know the density of the central body to obtain the orbital period of the small satellite orbiting around it. The equation we're using in this approximation is a very simple one:

where:

• $T$ — Orbital period;
• $G$ — Universal gravitational constant; and
• $\rho$ — Mean density of the central body.

We can use this simple equation to calculate the orbital period of any satellite around any celestial body. For example, in the case of the Earth, the density is $5.51\ \mathrm{g/cm^3}$, which would give a period of $1.4063\ \mathrm{hours}$.

It is important to remember that as we move away from the surface of the Earth (or the central body) this approximation falls off. This is clearly visible when we consider that different satellites have different orbital periods. For example, the geostationary orbit and geosynchronous orbits. These orbits have an orbital period of exactly $1\ \mathrm{day} = 23.934446\ \mathrm{hours}$. The difference between the geostationary orbit and the geosynchronous orbit is the position with respect to the equator.

The geostationary orbit is exactly above the equator, so the satellites in this orbit stay all over the same point on Earth's surface.

The geosynchronous orbit, however, can be located anywhere and doesn't have a one-to-one mapping of any particular point on the Earth.

You are probably wondering how many satellites orbit the Earth currently. We have the answer! Space debris is a big problem due to how many satellites orbit the Earth at the moment, and the number is only increasing. Nowadays, it is becoming such a problem that space agencies are starting to consider possible solutions to be implemented in the near future.

But enough rambling, let's give you the figure; just how many satellites orbit the Earth? The latest statistics point at over 3700 satellites orbiting the Earth right now, of which only about 1100 are operative.

We now should move to the binary star systems. We have already seen what is the binary star definition, namely, a system made of two stars of similar size orbiting each other. It's now time to calculate their orbital period. For this purpose, we made the second part of the orbital period calculator. We have several variables there:

• First body mass: The mass of the first star $M_1$;
• Second body mass: The mass of the second star $M_2$;
• Semi-major axis: The semi-major axis of the elliptical orbit with one star at the focus. We'll call it $a$; and
• Period: Orbital period of the binary star system $T_{\mathrm{binary}}$.

The orbital period equation ruling this system is the following:

where once again $G$ is the universal gravitation constant.

This equation is not limited to systems that fully comply with the binary star definition; it can be extended to any binary system. One such example is the Pluto-Charon system; none of these bodies are stars (not even planets) and hence do not fulfill the binary star definition. Yet they are a binary system for which we can compute the orbital period using our orbital period calculator.

In fact, this binary star system calculation is a much better approximation and could be extended to systems that wouldn't typically be considered binary systems. For example, if we take the Sun and Earth, we could still obtain reasonable results. By inputting $M_1 = M_{\odot}$ (mass of the Sun), $M_2 = M_{\oplus}$ (mass of Earth), and setting $a = 1\ \mathrm{au}$ as the mean distance between Sun and Earth, we obtain an orbital period of $T_{\mathrm{binary}}= 365.2\ \mathrm{days}$, which is $1\ \mathrm{year}$, almost to the minute.