Centripetal Force Calculator

Welcome to the centripetal force calculator. This simple-to-use tool helps you find answers to the most common and intriguing questions about the centripetal force. Have you ever wondered:

• What is the centripetal force?
• How to calculate the centripetal force?
• How to find the centripetal force acting upon a body in circular motion?
• Centripetal force vs. centrifugal force – what is the difference?

If so, this is the right place to begin! Let's go through the article together to learn about the centripetal force definition and centripetal force units. You can also find a couple of centripetal force examples to compute by yourself.

The book definition of centripetal force tells us that it's the force that acts on any object that moves along a curved path. The direction of the force is always parallel to the curvature's radius r.

Usually, we deal with centripetal force examples when talking about a circular motion. It's the simplest type of nonlinear movement. In this case, the curvature's radius is, naturally, the circle's radius. Check Omni's circular motion calculator for a more detailed explanation with examples!

We can write the centripetal force formula as:

F = m × v² / r,

where:

• F is the centripetal force;
• m is the mass of the object;
• v is its velocity; and
• r is the curvature's (circle's) radius.

According to Newton's second law, a = v² / r is the centripetal acceleration formula.

Take a look at the centripetal force's diagram to visualize what centripetal force definition is all about:

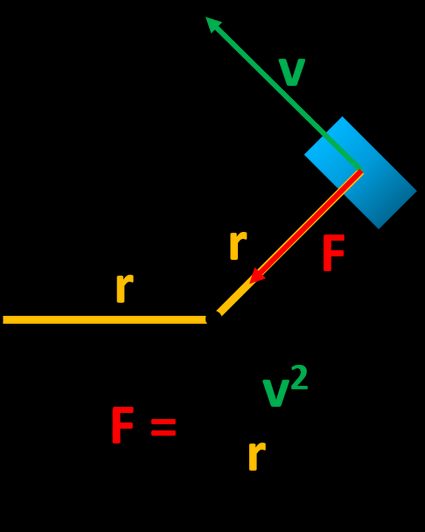
We can also use the angular velocity calculator to rewrite the centripetal force equation by replacing the velocity with the angular velocity ω:

F = m × ω² × r.

As the centripetal force is, well, a force, it has precisely the same unit as other forces in physics. So what is the centripetal force unit?

• The SI unit of centripetal force is the Newton, N;
• The imperial unit of centripetal force is the poundal, pdl;
• The English Engineering unit of centripetal force is the pound-force, lbf;
• The CGS unit of centripetal force is the dyne, dy.

However, using our centripetal force calculator, you don't have to worry about force unit conversion. You can change them automatically with a single click!

Similarly, the unit of centripetal acceleration is m/s².

At first glance, it may seem that there is no difference between centripetal and centrifugal force. Our centrifugal force calculator uses precisely the same equation as for the centripetal one:

F = m × v² / r.

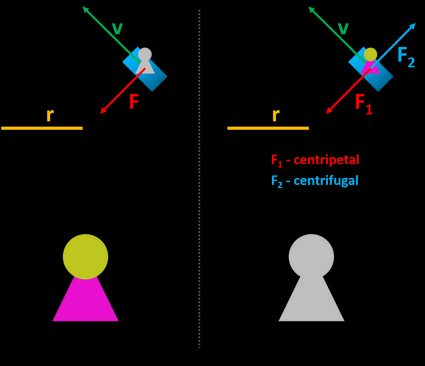
The crucial factor that helps us distinguish between these two is the frame of reference. Imagine a circular motion, e.g., a kid on a merry-go-round:

1. In an inertial reference frame (a parent watching the kid from a distance), there is only one force that changes the movement direction – the centripetal force;

2. In a non-inertial reference frame (the kid's point of view), there are two corresponding forces of the same values that balance each other. Once again, there is the centripetal force acting towards the rotation center. The second one is the centrifugal force – the representative of the force of inertia.

As you can see, the centripetal force is present in both reference frames, while the centrifugal force unveils only in the non-inertial one.

It isn't always evident whether we're dealing with an inertial or non-inertial frame of reference. How to distinguish between them? Let's take a look at the two diagrams with the comparison of centripetal vs. centrifugal force:

Having the theory in our minds, let's try to solve a few centripetal force examples.

1. How to calculate the centripetal force acting on a car that goes around a circular track? The car's mass is 2 t, its velocity equals 45 km/h, and the radius of the track is 10 m:

   • Before we do the computations, let's convert the mass to kilograms and switch the speed units from km/h to m/s. 2 t = 2000 kg, 45 km/h = 12.5 m/s;

   • Apply the centripetal force equation, F = m × v² / r = 2000 × (12.5)² / 10 = 31,250 N;

   • We can also write the solution using scientific notation, F = 3.125×10⁴ N, or with a proper suffix, F = 31.25 kN.

2. Let's find the velocity of an object that travels around the circle with radius r = 5 ft when the centripetal force equals 3.6 pdl. Its mass is 2 lb:

   • Rearrange the centripetal force formula to estimate the square of velocity. To do so, multiply both sides of the equation by r and divide by m;

   • v² = F × r / m = 3.6 × 5 / 2 = 9;

   • Work out the square root of the previous outcome to get the velocity, v = √9 = 3 ft/s;

   • We can also rewrite the result with a different unit. After rounding to three significant figures, the velocity equals 0.914 m/s.

Whenever you get lost or just want to check the results, feel free to use our centripetal force calculator. It follows precisely the same steps as in these centripetal force examples so that you can evaluate any of the centripetal force equation variables!

We can also rewrite the centripetal force definition so that the force's direction is always perpendicular to the motion.

Now, let's recall the work's definition:

W = F · s.

If the angle between the motion's displacement s and the force F is 90°, then the work equals zero, so no additional energy enters or emerges from the system. What is the consequence?

If the centripetal force is the only one that acts on the object, the system's total energy is conserved. Some of the best-known examples of this kind are planetary systems. That's why planets orbit around the Sun in stable orbits for ages.