Circular Motion Calculator

Omni's circular motion calculator allows you to calculate all the parameters of uniform circular motion. If you don't know what uniform circular motion is or feel overwhelmed by circular motion formulas, worry not! Our circular motion calculator will help you understand the concepts of uniform circular motion in physics.

Read on to know the definition, examples, and formulas of circular motion. You will also find examples of how to calculate circular motion parameters (like period, frequency, velocity, and acceleration) using our uniform circular motion calculator.

If you are more interested in determining the rotational momentum of an object, visit our angular momentum calculator.

When an object moves in a circular path, we call its motion circular. Some common examples of circular motion are:

• A race car moving on a circular curve;
• An artificial satellite revolving around the earth;
• The tip of the minute/second hand of a clock; and
• Whirling a stone tied to a string.

The circular motion of an object can be either a uniform circular motion or a non-uniform circular motion.

In a circular motion, the direction of motion changes continuously. At any instant, the direction of motion of a body moving in a circular path is along the tangent to the circle at that instant.

An easier way to visualize this concept is to imagine whirling a stone tied to a string; when the string breaks, the stone flies in a tangential direction.

In a uniform circular motion, the object moves on a circular path at a constant speed. This means that the object will cover equal distances on the circumference of the circle in equal intervals of time. In non-uniform circular motion, the speed of the object changes.

Although the speed is constant in a uniform circular motion, there is a continuous change in the direction of motion, as we discussed in the previous section. Hence, the velocity of an object undergoing uniform circular motion also changes continuously (see Figure 1).

Due to the change in the direction of the velocity, the object undergoes an acceleration called centripetal acceleration.

From Newton's first law of motion, we know that a body cannot change its direction of motion by itself. An external force is required for this purpose. This external force that keeps an object moving along a circular path is called centripetal force. You can explore more about this force in our centripetal force calculator.

Let us see how to use the uniform circular motion calculator to calculate the various physical parameters of circular motion.

1. Use the drop-down menu to select the set of parameters you want to calculate. We will select the option radius, speed, and acceleration as we want to calculate all the parameters for this example.
2. Enter the time period of circular motion, say 4 seconds in row 1.
3. The calculator will display the frequency (0.25 Hz) and angular velocity (1.571 rad/s) of the circular motion.
4. Type the radius of the circular path, say 2 meters, in row 2. The calculator will show the speed (3.142 m/s) and centripetal acceleration (4.935 m/s²).

We also recommend checking our centrifugal force calculator.

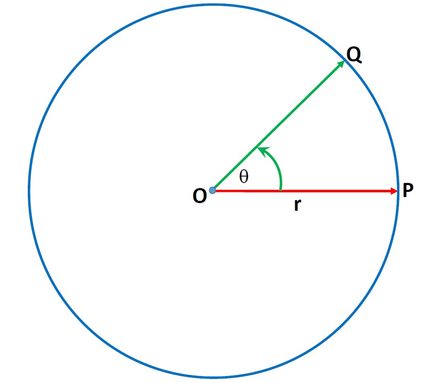
Let us consider an object moving along the circumference of a circle with radius $r$ (see Figure 2) and center at O. Let the object move (in an anti-clockwise direction) from P to Q in time $t$. The physical quantities that describe this motion and the formulas for circular motion are:

• Angular displacement ($\theta$) is the angle $\theta$ traced out at the center by the radius vector in a given time. We know that:

  $\rm angle = arc/radius$

  …hence, for Figure 2, we can then write:

  $\theta = PQ/r$

  The SI unit of angular displacement is radian ($\text{rad}$).

• Time period ($T$) is the time taken by the object to complete one revolution on the circular path. The SI unit of the time period is the second ($\rm s$).

• Frequency ($\nu$) is the number of revolutions the object completes in one second. The SI unit of frequency is hertz ($\rm Hz$).

  $\nu = 1/T$

• Angular velocity ($\omega$) is the rate of change of angular displacement with time, i.e.,

  $\omega = \Delta \theta/ \Delta t$

  The SI unit of angular velocity is radian per second ($\rm rad/s$).

  When the object completes one revolution (see Figure 2), the angle traced at the center is $2 \pi$ radian. This means, for the time period of circular motion, $t = T$, $\theta = 2 \pi$. Hence we can express the angular velocity as:

  $\omega = 2 \pi / T$

  ...or:

  $\omega = 2 \pi \nu$

• Angular acceleration ($\alpha$) is the rate of change of angular velocity with time, i.e.,

  $\alpha = \Delta \omega/ \Delta t$

  The SI unit of angular acceleration is $\rm rad/s^2$.

• Centripetal acceleration ( $\alpha_c$) is the acceleration of an object undergoing uniform circular motion. It always acts on the object along the radius and towards the center of the circular path.

  $\alpha_c = v^2/r$