Angular Momentum Calculator

Did you ever find yourself wishing for an angular momentum calculator? We think we have all wished, at some point in our lives, that we had a calculator which would come and solve our physics queries. Well, don't worry, your wish has been answered with this calculator that tells you how to calculate angular momentum. Our angular momentum calculator is a user-friendly tool that allows you to find angular momentum in two ways, so you can use it with all the data you have gathered. We will also talk about the conservation of angular momentum and some examples. So, if you are wondering what angular momentum is and want to get into the nitty-gritty of it, read on!

If you want to calculate linear momentum instead, use our momentum calculator.

Angular momentum, occasionally referred to as the moment of momentum or rotational momentum, is the momentum of an object around its axis.
We know that the momentum of an object is referred to as mass in motion, which means that if a body or an object has some mass and is in motion, that object is said to have momentum. In this manner, we can summarize angular momentum as the rotational correspondent of linear momentum.

Similar to angular velocity, angular momentum has two distinct types:

• The first one is spin angular momentum, which is defined as the angular momentum of an object around its center of mass coordinate; and
• The second type is known as orbital angular momentum, which is the momentum of the center of mass about the origin. These two types sum up to give the total angular momentum of an object.

We have an angular velocity calculator that may help you understand its significance.

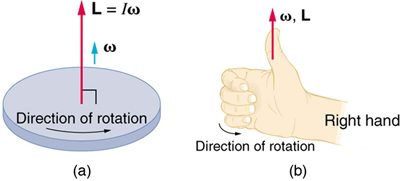
The direction of angular momentum is perpendicular to the object's plane of rotation. If you make a fist with your right hand and make your fingers curl in the same direction as the rotation, the direction of your thumb is the direction of the momentum.

To understand how to calculate angular momentum, besides using the angular momentum calculator, you need to be aware of the angular momentum formula.
Consider the planets all revolving around a central point, the Sun ☀️. These are all examples of an object moving around a central point. In this situation, the angular momentum is the product of the mass, $\text m$ & velocity, $\text v$, of the object, and the radius, $\text r$, of the circular path that the object is moving along. Hence, we can write the formula of angular momentum as:

$\text L = \text m \times \text v \times \text r$

The Earth's rotation on its axis is an example of a rigid body rotating on its axis. In this situation, the angular momentum is the product of the moment of inertia, $\text I$, and the angular velocity, $\text ω$.

$\text L = \text I×\text ω$

The angular momentum calculator uses both these formulas to calculate the angular momentum of an object for your ease.

Our moment of inertia calculator can be of assistance if you want to make more sense of the moment of inertia.

By using the formula for angular momentum, we can easily derive its units:

$\text L = \text m \times \text v \times \text r$

$\text L = \text {kg} ⋅ \text {m/s} ⋅ \text m$

$\text L = \text {kg} ⋅ \text {m}^2/\text s$

Hence, the unit of angular momentum is kg ⋅ m²/s.

From the unit of angular momentum, we can also derive its dimensions:

$\text L = \text {kg} ⋅ \text {m}^2/\text s$

$\text L = \text M \text L^2/\text T$

Angular momentum is the rotational equivalent to linear momentum.
They both comprise mass and displacement, whereas only angular momentum has the additional components of the position and shape of the object.
Linear and angular momentum obey the law of conservation, with slight variation, i.e., the linear momentum of an object is conserved if no resultant force acts on the system. In contrast, angular momentum remains conserved in the absence of torque.

The law of conservation of angular momentum states that if no external torque is applied to an object, the object's angular momentum will remain unchanged:

$\text {L remains constant when } \tau = 0$

This is how the law of conservation of angular momentum is expressed.

For any system to obey the law of conservation, an exchange of forces must occur so that the resultant force remains constant.
To understand this phenomenon, imagine an ice skater ⛸️ spinning on the tip of his skates. The torque applied to him is negligibly small because the friction between his skates and ice is minimal, and the friction is being exerted nearby the axis point. As the skater brings their arms and legs closer to their body, which is also the axis of rotation, they decrease their body's moment of inertia. If angular momentum is to remain constant (and it must), a corresponding increase in the rotational velocity must occur. That is how ice skaters are able to gracefully execute those marvelous spins that earn them their rapturous applause.

Let's look at a gyroscope as an example of angular momentum. It maintains its upright position while it spins. This is due to the conservation of angular momentum.

Have you ever wondered how satellites 🛰️ can orbit planets/the Earth without crashing into the planet itself? Yes, gravitational force plays a major role in this scenario. Since this gravitational force is always directed towards the center, or in this case, the planet and the satellites conserve the angular momentum by exchanging displacement and velocity as they revolve around the planet, they are able to convert the gravitation force into movement. The direction of a force towards the center of a system is an important concept known as central force motion, which is better analyzed using the concept of conservation of angular momentum.

Another example of conservation of angular momentum is a bowling ball hitting a pin 🎳.

Let's take a look at some examples of angular momentum where you have to calculate the angular momentum of an object.

Example no. 1
An object with a moment of inertia of 2 kg ⋅ m² rotates at 1 rad/s. What is the angular momentum of the object?

Given:
Moment of inertia = 2 kg ⋅ m²
Angular velocity = 1 rad/s

Required:
Angular momentum=?

Solution:
The given data suggests we find the solution using the formula:
L = I × ω

L = 2 × 1

L = 2 kg⋅m²/s

Example no. 2
A 3-kg particle rotates at a constant angular velocity of 2 rad/s. What is the angular momentum if the radius of the circle is 10 cm?

Given:
Mass = 3 kg
Radius = 10 cm = 10/100 = 0.1 m
Angular velocity = 2 rad/s

Required:
Moment of inertia =?
Angular momentum =?

Solution:
The given data suggests we find the solution using the rotatory body formula for angular momentum:
L = I × ω
But first, we need to determine the moment of inertia for the particle using the formula:
I = m × r²

I = 3 × (0.1)²

I = 3 × 0.01

I= 0.03 kg⋅m²

Now,

L = I × ω

L = 0.03 × 2

L = 0.06 kg⋅m²/s

We hope that these examples help you to understand how to calculate angular momentum with any given data.

Speaking of angles and angular concepts, are you aware of angular displacement? Check out our angular displacement calculator if you are interested.

There are many other fields where angular momentum plays a significant role:

• Center force motion;
• Angular momentum and torque;
• Orbital mechanics;
• General relativity;
• Quantum mechanics;
• Electrodynamics;
• Optics;
• Spin (atomic physics); and
• Conservation of angular momentum in the law of areas