Angular Velocity Calculator

This angular velocity calculator is a simple-to-use tool that gives an immediate answer to the question, "How to find angular velocity?". In the text, you'll find several angular velocity formulas, learn about different angular velocity units, and, finally, estimate the Earth's angular velocity!

Have you ever wondered what the relationship between angular velocity and angular frequency is? Or where is angular velocity applied? Read on to find out, and become an expert in the field of circular motion.

Angular velocity describes the rotational movement of bodies. It measures how fast they move around some center of rotation. We can think about two different kinds of rotations. The first one describes the motion of the center of mass of a given object around a specific point in space, which we can describe as an origin. Some examples include planets moving around the Sun or a car taking an exit on the highway.

The second one is about the rotation of the body around its own center of mass – the spin (not to be confused with the quantum property of particles, also called spin). Surely you've seen a basketball player spinning a ball on his finger.

Generally, we can say the faster the movement, the higher the angular velocity. We have to move on to the angular velocity equations described in the next section to define some specific values.

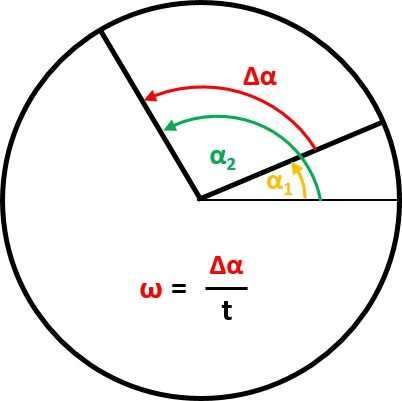
This angular velocity calculator uses two different angular velocity formulas depending on your input parameters.

The first angular velocity equation is analogous to the equation for linear velocity:

where $\alpha_1$ and $\alpha_2$ are two values of angles on a circle, and $\Delta\alpha$ is their difference. $t$ is the time in which the angle change occurs. As you can see, for the normal velocity, there is a ratio of the positional shift in a period, while here, we use angle instead of distance.

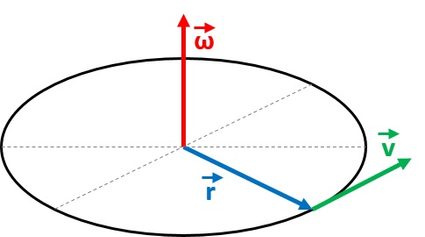
We can derive the second angular velocity formula from the relation of the linear velocity and the radius using the cross product, which is:

We can rewrite this expression to obtain the equation of angular velocity:

where all of these variables are vectors, and $|r|$ denotes the absolute value of the radius. Actually, the angular velocity is a pseudovector, the direction of which is perpendicular to the plane of the rotational movement.

There are multiple units of angular velocity, and the ones that we use in our angular velocity calculator are mentioned below:

• rad/s or radians per second — The definition comes straight out of the first angular velocity formula. It tells how big the rotation (or angle) is that the body moves through in a given time.

• RPM or revolutions per minute — The unit found most frequently in practical application. Using it, you can describe how fast a wheel or engine spins. You can easily imagine the difference between 10 and 100 RPM.

• Hz or hertz — The same units used for frequency but rarely used in the context of angular velocity. It is somewhat similar to RPM, telling us how many complete rotations are made in a given time. The difference is that previously, the basic unit of time was a minute, and here it is a second.

Naturally, all of these angular velocity units converted between one another using the following relations:

1 RMP = 0.10472 rad/s = 0.01667 Hz

Or the other way around:

1 Hz = 6.283 rad/s = 60 RPM

Have a look at the definition of angular frequency:

where $f$ is the frequency. As we can see, it is denoted by the same letter. Additionally, the unit of angular frequency is rad/s, precisely the same as for the angular velocity. So the question may arise: "What is the difference between angular velocity and angular frequency?".

The answer is relatively simple. The relation between angular frequency and angular velocity is analogous to the one between the speed and the velocity. The first one is a magnitude of the latter; in other words, angular frequency is a scalar, whereas angular velocity is a (pseudo)vector.

We commonly use angular frequency when talking about a harmonic motion, an example of which is a simple pendulum. As you can imagine, the motion doesn't have to be represented by a standard rotation, just a movement that periodically repeats its position. The angular velocity, however, is strictly connected with the motion around some point. Therefore, we can say that angular frequency is a more general quantity, and we can use it to describe a wide range of physical problems. In contrast, angular velocity includes only rotational movement.

How about we make use of our angular velocity calculator? Let's estimate the angular velocity of the Earth! Firstly, we consider the spinning velocity. We know that the Earth is making a full rotation, with respect to distant stars, in about 23 h 56 min 4 s, which is roughly 23.934 h. The entire rotation is the angle 2π rad, so the resulting angular velocity is:

or $7.292 \times 10^{-5}\ \rm rad/s$ (using scientific notation).

Now that we know the spin angular velocity of the Earth, we can evaluate its linear velocity at the equator. To do so, we need the Earth's radius, roughly 6 371 km. The only thing we have to do is to insert values into the second formula of angular velocity:

To work out the linear velocity with respect to the center of the Earth, all you need to do is multiply this result by the cosine of the latitude of your city.

By the way, have you ever wondered why rockets usually launch from spaceports placed near the equator and not from the poles? Well, almost a 500 m/s boost at the beginning is a considerable fraction of its final velocity. So moving the start point as close to the equator as possible reduces the amount of fuel needed to accelerate the rocket.

After that, we can ask once again how to find Earth's angular velocity, but this time the orbital one. All the calculations are analogical, but we have to change the time from 23.943 h to one year, which is about 365.25 days. The angle change is the same, the complete revolution.

and the linear velocity of the Earth with respect to the Sun (for the average radius $\small 1.496\!\times\!10^8\ \rm km$) is:

We are moving pretty fast, aren't we?

Multiple physical quantities are related to angular velocity, some of which are listed below:

1. Angular acceleration — Describes how the angular velocity changes with time. The higher the difference in angular velocities, the bigger the angular acceleration value. Feel free to check how it works in practice with our angular acceleration calculator.

2. Rotational kinetic energy — The measure of energy in a circular motion. As with kinetic energy, the dependency of (angular) velocity is quadratic.

3. Centripetal force — It's the force that keeps you turning or rotating; in circular motion. In a car turning, the tires are exerting this force. The tendency to keep moving straight (Netown's first law) is called inertia, sometimes called the centrifugal force even though it is not a real force.

4. Coriolis effect — This causes objects to turn if they reside on a rotating body (e.g., on the Earth) instead of moving in a straight line.

5. System of pulleys — This is not a physical quantity, precisely speaking, but it is an interesting device that is all about angular velocity. The simplest system consists of two pulleys, usually with different circumferences or radii. A belt connects them, so their linear velocities are identical, but since they are of various sizes, their angular velocities change proportionally.

   Knowing this and having some engine with well-defined rotational velocity, we can set the angular velocity of the output element with good precision simply by adjusting its size.

A few fundamental rules tell us about the quantities conserved in isolated systems. The best known are the conservation of energy and the conservation of momentum. Together with them, there is also the conservation of angular momentum. If we think of two moments in time, we can write the rule as:

where $I_1$ and $I_2$ are the initial and final mass moments of inertia, respectively; these quantities describe the distribution of mass concerning their respective centers of rotation.

We can see that if the moment of inertia increases, the angular velocity decreases, and vice versa. So, what are the consequences of this phenomenon?

Let's imagine that you are a figure skater. When you rotate, you possess some angular velocity. If your arms are wide open, the mass moment of inertia is relatively big. Then, you move your arms close to the rest of the body. As a consequence, your moment of inertia decreases, so because the overall angular momentum has to be conserved, your angular velocity increases — it means you will spin faster! This is no magic, just physics!

If you can't / don't like skating, you can try to verify the rule with a usual swivel chair. Just remember, safety first! Make sure there is enough space to do this experiment. After that, simply start spinning and see how your angular velocity changes when you move your arms back and forth. Additionally, you can increase the effect by using some dumbbells. As a result, you can combine both exercise and fun into one thing!