Bessel Function Calculator
Are you struggling to calculate or validate Bessel function values? Do you wish you could plot the Bessel function to get that extra information? If your answer is yes, you've come to the right place because our Bessel function calculator does everything for you!
Bessel functions are fairly advanced mathematical topics that can be perplexing to anyone. This article covers the basics, such as the Bessel differential equation, how to calculate Bessel functions of the first and second kinds, and the recurrence relations for Bessel functions, so you're well equipped to solve your problem using Bessel functions.
Bessel functions and its differential equation
Bessel differential equation is a second-order differential equation given by:
Here is an arbitrary complex number.
Since this is a second-order differential equation, there have to be two linearly independent solutions. We call these solutions Bessel functions of the first and second kind. All Bessel functions are also commonly referred to as cylinder functions.
The order of the Bessel function is given by , and although it can be an arbitrary complex number, the most critical cases are when is an integer or half-integer. In this calculator, we shall exclusively use real-valued , but can be complex.
You can refresh your knowledge of complex number operations using our complex number calculator.
How do you calculate the Bessel function of the first kind?
We use the following power-series to evaluate the Bessel function of the first kind:
where:
- — Bessel function of the first kind;
- — Order of the Bessel function;
- — Arbitrary real or complex number; and
- — Gamma function.
Gamma function is an extension of the factorial calculation to non-integer values. You can learn more about this using our gamma function calculator.
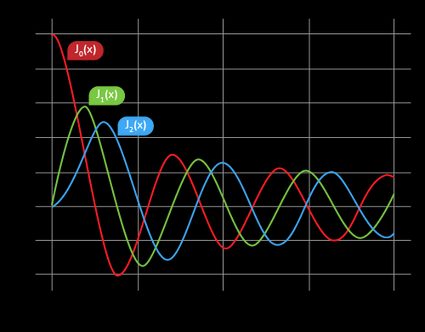
For non-integer , the functions and are linearly independent. However, for integer , they're related as follows:
💡 For computation, it is impractical to expand this series to . We should get sufficiently precise values after a finite number of iterations.
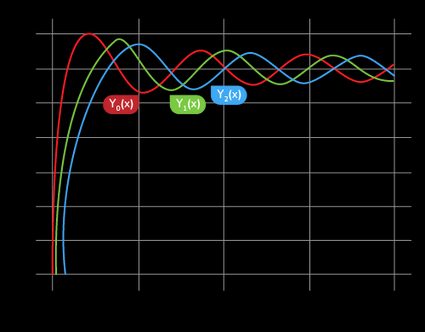
How do you calculate the Bessel function of the second kind?
Computing the Bessel function of the second kind is tricker than because it has different formulae for different .
To evaluate the Bessel function of the second kind for non-integer , we use the formula:
where is the Bessel function of the second kind of order .
If the order is an integer , we should take the limit of as the order approaches the integer :
For non-negative integer , this limit reduces to:
where is the digamma function, the logarithmic derivative of the gamma function :
If you're groaning at this complexity, we have some good news! Since we're using exclusively for non-negative , we can use a simpler formulation for the digamma function, given by:
where:
- – harmonic number; and
- – .
But what about negative integer ? Again, we have some good news! Similar to , also follows the relation:
which we can utilize to calculate from .
How do you calculate Hankel functions?
The Bessel functions of the third kind, also known as the Hankel functions, are two linearly independent solutions to the Bessel differential equation. We express them as linear combinations of the first two kinds of Bessel functions:
where:
- – The Hankel functions; and
- – The imaginary unit.
Recurrence relation of Bessel functions
The Bessel functions we discussed so far exhibit the following recurrence relations:
where:
- – Any cylinder function, i.e., or ;
- – Derivative of any cylinder function; and
- – Any arbitrary real or complex number.
In particular:
You can use these recurrence relations for Bessel functions to calculate the derivatives of the desired Bessel function quickly.
How to find Bessel function values using this Bessel function calculator
This Bessel function calculator will solve for Bessel functions of the first, second, and third kind simultaneously. All you need to input are the order and , the point at which you desire to evaluate. Keep in mind that:
- The order must be a real number;
- The number can be real or complex; and
- This Bessel function calculator will plot the Bessel function of the first two kinds, as long as the number is a real number.
Note that the order must be within the range to keep the computational time to a minimum. Any higher order will cause noticeable lag in most computers.
Also, the must be within the range to maintain computational accuracy since there is a different method for calculating Bessel functions for large .
If you wish to perform calculations beyond these limits, please get in touch with us!
FAQs
How do I calculate bandwidth with Bessel function table?
To estimate bandwidth using a Bessel function table, you must know the modulating index β and modulating frequency fm:
- Find the minimum value of Jᵥ(β) above 0.01 (or any value deemed the minimum significant value) by referring to a Bessel function table.
- Determine the number of sideband pairs N in the signal, equal to the order v of the Bessel function Jᵥ(β).
- Substitute N and fm in the formula B = 2fmN to get the bandwidth B.
- Be proud of yourself for solving a not-so-simple problem in a not-so-complex manner!
What is the maximum value of the Bessel function of the first kind?
J₀(0) = 1 is the maximum value of the Bessel function of the first kind. It occurs when the order ν = 0 and x = 0. To calculate this, follow these steps:
- Substitute ν = 0 and x = 0 into the integrand cos(ντ - x sin(τ)) to get cos(0) = 1.
- Evaluate the integral ∫1 ∙ dτ to get [τ].
- Apply the lower limit 0 and the upper limit π to [τ] to get [π-0] = π.
- Divide by π to get π/π = 1.
- Verify this result using Omni's Bessel function calculator!
Where do the singularities lie for the Bessel functions?
For negative non-integer orders, the Bessel function of the first kind has a singularity at x = 0. For all orders, the Bessel function of the second kind has a singularity at x = 0.
Are Bessel functions periodic?
The Bessel functions are not periodic, although they look like decaying sine or cosine waves on a graph.