Angle of Depression Calculator
Table of contents
What is the angle of depression? Angle of depression definitionThe angle of depression calculator. How to find the angle of depression?Sample calculation of finding the angle of depressionWant to learn more?FAQsThis angle of depression calculator determines the angle by which an inclined line deviates from the horizontal towards the downward direction. Like in our elevation grade calculator, this calculator uses the concept of an angled line's slope.
In this calculator, you will learn about:
- What the angle of depression is;
- How to find the angle of depression; and
- How to use this angle of depression calculator.
After reading this text, you will find the angles of depression everywhere with the angle of depression formula. Let's get started!
🙋 If you want to dive deeper into the mathematical concept of slope, our slope calculator is for you.
What is the angle of depression? Angle of depression definition
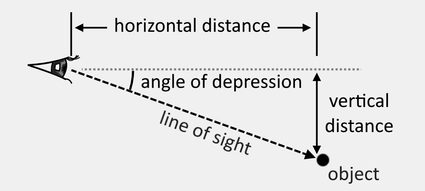
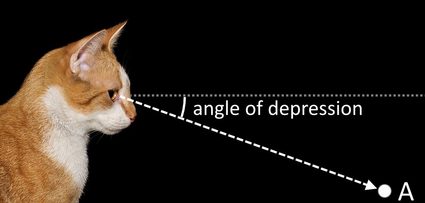
The simplest angle of depression definition is that it is the angle between the horizontal and the part of a line that is below the horizontal. In the image below, as the cat looks downwards towards point A, it creates a certain angle of depression from the horizontal.
Sometimes we may also see the angle of depression used to express the slope of a surface such as a mountainside or a roadway. However, for such information, we typically use the counterpart of the angle of depression – the elevation grade.
The angle of depression calculator. How to find the angle of depression?
Since we now know what the angle of depression is, let's learn how to find it! We can determine the angle of depression using surveying equipment like an engineer's transit or a clinometer. These devices are optical instruments that have angle-measurement features and can instantly give us the angle that we need. However, we can also use mathematics to find the angle of depression. But first, we need to know two distances: the horizontal distance between the viewer and the object, and their vertical distance, as shown in the illustration below:
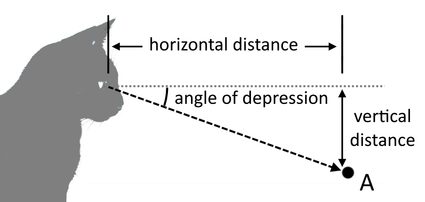
If you already have the values of these measurements, you can now input them into our angle of depression calculator. To do it manually, substitute these values in the angle of depression formula, which is derived from the arctangent function in trigonometry.
We use the arctangent function because, if we look closer at the dimensions concerned, we can see that we have actually formed a right triangle and that we are dealing with the sides adjacent and opposite to the angle we are interested in. With that said, below is the angle of depression formula:
angle of depression = arctan(vertical distance / horizontal distance)
Sample calculation of finding the angle of depression
Time for an angle of depression example. Suppose we need to find the angle of depression, α, of the boy's line of sight from the top of the slide towards the girl at the bottom of the slide, as shown in the illustration below. We can see that the horizontal distance between the children is 3.0 meters and the vertical distance between their line of sight is 1.5 meters.
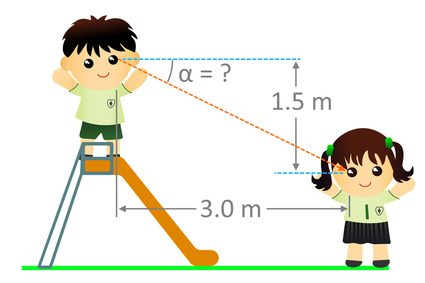
Using the angle of depression formula, we calculate angle of depression α as follows:
α = arctan(vertical distance / horizontal distance)
α = arctan(1.5 meters / 3.0 meters)
α = arctan(0.5)
α = 26.56505118° ≈26.565°
From the calculation above, we can now say that the angle of depression, α, is around 26.565° from the horizontal.
Want to learn more?
If you are given the angle of depression and at least one of the distance measurements (either horizontal or vertical distance), we can also calculate the other parts of the right triangle formed using the sine, cosine, and tangent functions. You can learn more about this in our right triangle calculator.
Is angle of depression equal to the angle of elevation?
Yes. If two people were staring at each other from different heights, the angle that the person above would need to look down by would be equal to the angle that the person below would need to look up by. In a diagram, this would be represented as alternate angles in a transversal line.
What is the maximum angle of depression?
90° is the maximum angle of depression. The angle of depression must be less than or equal to 90°. A 90° angle of depression would be equivalent to looking straight down at an object.
How do you find distance using angle of depression?
To find the distance between two points at different elevations using the angle of depression, follow these steps:
- Measure the vertical distance, or difference in altitudes,
a. - Measure the angle of depression,
α. - The line-of-sight distance is then
d = a / sin(α). - Alternatively, you have the horizontal distance,
b. You can find the distance usingd = b / cos(α).
What instrument is used to measure the angle of elevation?
An inclinometer is used to measure the angle of elevation. This device measures angles of depression/elevation with respect to the force of gravity at a particular location by using an accelerometer.
