Dice Average Calculator

If you wondered how to calculate the average dice roll, our dice average calculator is the right tool for you! A die is a standard tool for generating random numbers in various games and activities.

While calculating the average of a d6 (6-face die) may be straightforward, it can become more challenging with, for example, the average of a d10 (10-face die). This is where the dice average calculator comes in handy, providing an efficient and accurate way to calculate the average of a selected set of dice rolls.

Read the following article to learn about the average dice roll formula and check the dice average chart!

Before we go into how the dice average calculator works, let's first define what we mean by average. In statistics, the average (or mean) measures the central tendency or the value most representative of a data set.

To calculate the mean of a group of numbers, you add all of them and divide by the total number of values. To understand it better, you can check our average calculator or mean median mode calculator to learn about different central tendency measures.

What exactly is the average value when it comes to the dice roll? When we say the average of a d6 is 3.5, it means that, on average, over a large number of rolls, the expected value of dice would be 3.5.

However, it's important to note that a single roll of a fair six-sided die can only result in one specific outcome (i.e.,1, 2, 3, 4, 5, or 6) and may not necessarily match the calculated average. The average is a statistical concept representing the expected value of several dice rolls over many repeated trials.

Calculating the average by adding values and dividing by the total number is a general approach. However, calculating the dice average is a special case when a different formula may be applied. If you want to sum a simple sequence of 1 + 2 + 3 + 4 + ... + n, you can use this simple and elegant average dice roll formula:

where:

• $m$ — dice average;
• $h$ — the highest value (for example, for a 12-sided dice, the highest value is 12).

Since we want to calculate the average of any number of dice, we should adjust the above dice average formula by multiplying the result by the total number of dice $n$:

Using the dice average calculator is extremely simple:

1. First, select the type of die you are using. We will show you the die and its expected value.
2. Then, enter the number of dice you will be rolling.
3. And that's it! You can immediately see the result. The dice roll average is what you were looking for.
4. At the bottom of the calculator, you can see the standard deviation of your average as well.

To roll three six-sided dice, for instance, you can select Cube (6 faces) from the dropdown menu and enter 3 in the Total number of dice field. The calculator will then show 10.5 as the average value of your rolls. If we have just one die, the average of a d6 is 3.5, and so for three dice, we multiply by 3, which gives 10.5.

Or do you want to get an average of a d10 roll? So select Deltohedron (10 faces) and determine how many dice you want to use.

We prepared the following dice average chart for quick access whenever you need it. Remember, you can use the dice average calculator to get the same results!

Have you noticed that most dice have an even number of sides? This is one of the reasons why some of the dice roll averages we calculate in the dice expected value calculator are not integers, for instance, $3.5$ as an average of a d6 or $10.5$ for three such dice. Let's see the examples that should explain why it happens like that.

Rolling one 6-sided die can result in six possibilities from 1 to 6. The probability of getting a specific value is the same for all of them and is equal to:

These equal chances allow us to find the simple average of the numbers, which is:

Now, what happens if you roll three d6? You need to:

1. Take into account all the possibilities of $6^3 = 216$;
2. Sum up the values on the three dice and write down the results;
3. Count how many times you obtain a specific sum;
4. Select the two sums that appeared most frequently; and
5. Find their average... or use the die average calculator.

The two most probable sums are $10$ and $11$ (the average is $10.5$) that were rolled out $27$ times each, which is $12.5\%$ of all cases. Next, the sums $9$ and $12$ have a $11.57\%$ chance of occurring ($25$ times), $8$ and $13$ have a $9.72\%$ chance of occurring ($21$ times), and so on with other numbers having smaller chances.

The important thing is that when you roll three dice, the sums should be somewhere around $10$ and $11$ in most cases. At the bottom of the dice average calculator, we also calculate the standard deviation, which measures the dispersion of the sums around the average value. For three d6, the standard deviation equals $2.958$.

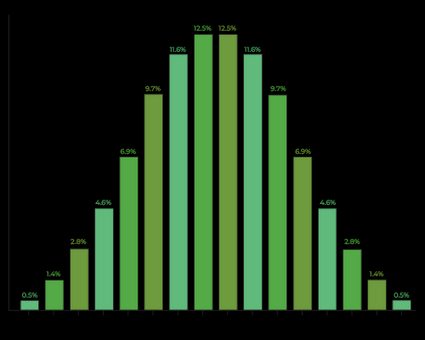
Check the below histogram showing the frequency of finding the sums of three dice, which is very similar to the Gaussian distribution explained in the normal distribution calculator. In fact, when you increase the number of rolls, you will quickly approach this distribution!

There are plenty of possible applications of the average dice roll calculator:

• You can use it for educational purposes to better understand statistics and probability, especially if you combine it with using the dice probability calculator.

• In games, you can use the dice expected value calculator to determine a weapon's average damage output or a monster's average hit points.

• When preparing your own game, the dice roll average can be helpful in deciding which type of dice to use in an activity.

Don't have a physical dice within reach? No worries! You can always use our dice roller, which allows you to use many different types of dice.