Radar Horizon Calculator

Radars revolutionized the war and then our daily lives: let's learn how far they allow you to see with our radar horizon calculator.

Radar technology may sound complex, but it relies on simple physical phenomena, and its use is limited by the geometry of the planet we live on. Here you will learn:

• What is a radar?
• How far does a radar see?
• What is the radar horizon formula?
• How to calculate the radar horizon?

We'll also see some examples of radar horizon distance. Keep reading, don't wait for the return signal!

Radar, the acronym for "radio detection and ranging", is a technology that uses radio frequencies to detect objects at a distance using the reflection principles. The core concept is to have a transmitter (that sends radio waves in a particular direction) and a receiver (that listens to the reflected "echoes").

Radars had been under development for a few decades before WWII, but only with the conflict brewing (and then exploding) did the technology really take off. Its invention helped fight the Germans during the Battle of England and proved its invaluable importance.

Once the war ended, radar technology (like many other wartime inventions) was made available to the public, offering its services for peaceful purposes. Instead of detecting enemy planes and ships, the radar started helping in weather forecasting and civilian transport. In recent years, the automotive industry has been eyeing the radar for application in autonomous vehicles, where the radar's detection ability will help avoid collisions.

The distance at which radars can detect a target limits its usefulness. To calculate such distance, we need to take into account some basic geometric considerations, which we can complicate further to obtain a more lifelike result.

The first important parameter to keep in mind is the height of the emitter. The higher, the better. This parameter uniquely identifies the distance at which the radar can see the surface of the Earth. But since Earth is (almost) spherical, a radar can see further than that. How? Let's introduce the target.

An airplane flying over the ground can still be visible to a radar if its height is higher than a certain value. But below the "line of sight" of the radar, the Earth's curvature would effectively hide it. That area is known as the shadow zone. A similar concept applies to our sight, too: discover it with our Earth curvature calculator!

Radars suffer from another problem: the portion of the projected energy from the transmitter closer to the ground meets the various interferences caused by turbulence, bird flocks, and other factors. This phenomenon causes, in turn, a set of return echoes that pollute the signal received by the radar. We call that area clutter zone: a target moving in that area would be hard to detect!

Making simple geometrical deductions deliver ideal values for the radar horizon: to obtain accurate results, we need to introduce a correction that considers the atmospheric refraction.

The air density drops with altitude, and with it, the index of refraction of that layer of atmosphere (it depends on the temperature: learn about it at our temperature at altitude calculator). Consequently, the radio waves are effectively bent downward (almost following the Earth's surface) allowing radar to illuminate targets beyond the geometrical horizon. In the radar horizon formulas, this phenomenon is represented by a corrective factor of $4/3$ applied to the Earth's radius: radars effectively "see" as if they were on a larger planet!

The radar horizon formula comes in two flavors: ignoring the atmospheric refraction or not. The first case is easier to understand, but yields less accurate results. The second case introduces a correction and delivers results that agree with radars used in the field.

Let's analyze the first case.

We can calculate the radar horizon with a simple application of the Pythagorean theorem (learn how to calculate it with our Pythagorean theorem calculator). If we consider the Earth a perfect sphere with radius $R_{\text{E}}=6,371.009\ \text{km}$, and we place a radar at height $h_{\text{r}}$ on the Earth's surface, we can imagine we've created a right triangle with hypotenuse $R_{\text{E}}+h_{\text{r}}$ (from the Earth's center to the radar) and one side $R_{\text{E}}$ (from the Earth's center to the surface). The remaining side is the radar's geometrical horizon (the distance it can see) and we name it $d_{\text{r}}$:

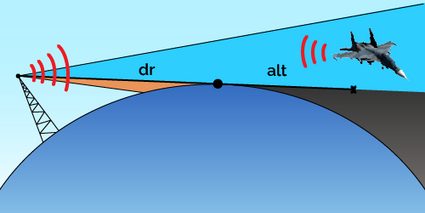
Consider now a target flying at height $h_{\text{t}}$ over the sea level. We can find the maximum distance at which our radar can spot it by applying the same reasoning: we call it target visibility.

The small height correction we applied before for the radar horizon distance works here, too: if the target flies low enough, we can write $d_{\text{t}}=\sqrt{2 R_{\text{E}} h_{\text{t}}}$.

Summing the two values of the horizons gives us the maximum distance from the radar at which we can identify the flying target: we call this distance $D$.

The correction introduced by the atmospheric refraction slightly changes the formulas we saw before. Considering the small height simplified formulas, we have:

The difference may be substantial!

Radar operators would love a flat Earth: their radar horizon would be theoretically limitless... How are we sure that Earth is round? Try our flat vs. round Earth calculator!

Example 1

Imagine you are flying on an E-3 airborne early warning and control (AWACS) aircraft, cruising at an altitude of $9,\!150\ \text{m}$ ($30,\!000$ feet). An enemy bomber is flying at $122\ \text{m}$ ($400$ feet) — using a terrain tracking radar, at what distance will we detect it?

Let's calculate the radar horizon and the target visibility with the modified radar horizon formulas:

The total distance is then:

Example 2

Imagine now that you are manning a radar station on the ground, with your antenna a mere $10\ \text{m}$ above the ground. The new distances would be:

We get a total of:

For a plane traveling at the speed of sound, the use of an early warning aircraft would give you more than 20 minutes before its arrival. This time would be reduced to a mere three minutes for the station on the ground: blink and you'll miss it!

What if the radar horizon is not enough for your detection needs? This problem surfaced during the Cold War, when the threat of missile attacks was high: the early detection of a launch of a naval unit or a bomber was considered a fundamental means of protecting a country's territories.

As we just saw, a "standard" radar has limits set by geometrical factors. Even an airborne radar can't see farther than a few hundred kilometers: radio waves must take another way. In over-the-horizon radars, the signal is directed toward the ionosphere, a radio-reflective layer of the atmosphere, which redirects them to the surface. The signal reflected by the eventual target is then re-reflected by the ionosphere and picked up by the receiver.

We created a useful and simple tool to calculate the radar horizon! You only have to select if you're considering the atmospheric refraction or not, and then insert your data. Moments later, you will learn the distances of the radar horizon and of the target visibility!