Doppler Effect Calculator

The Doppler effect calculator will help you analyze the changing frequency of sound you hear if either the source of sound or the observer is in motion. This article will explain in detail what is the Doppler effect and how to properly use the Doppler effect equation.

Imagine that you are standing on the sidewalk of a busy street. You can hear the siren of an ambulance approaching you. Once the ambulance passes you, the sound's pitch – in other words, its frequency – changes. The sound appears to be "lower" as its frequency decreases.

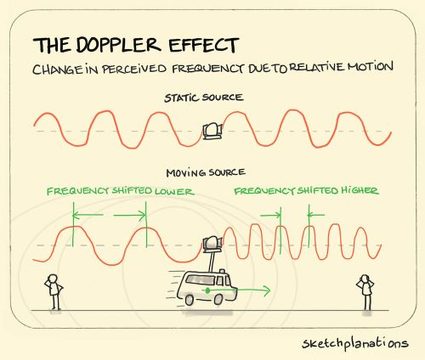
Why did that happen? Precisely because of the Doppler effect. Doppler hypothesized that if a source of waves moves relative to the observer, then the frequency of these waves changes (along with their wavelength). Learn more about waves in our wavelength calculator or our frequency calculator.

Doppler effect is widely used in medicine – it allows us to measure the blood flow in arteries and veins, perform ultrasound, and it also has a great purpose when dealing with how to calculate cardiac output with echocardiography doppler.

The Doppler shift can be described by the following formula:

where:

• $f$ – Observed frequency of the wave, expressed in Hz.
• $f_0$ – Frequency of the emitted wave, also expressed in Hz.
• $v$ – Velocity of the waves in the medium. By default, our Doppler effect calculator has this value set to 343.2 m/s, the speed of sound propagating in the air. For a more precise value, use our speed of sound calculator.
• $v_r$ – Velocity of the receiver. It is positive if the receiver is moving toward the source; and
• $v_s$ – Velocity of the source. It is positive if the source is moving away from the observer.

Let's analyze a more complex example of the approaching ambulance. You are riding a bicycle along the road, going in the same direction as the ambulance. You can hear the siren of the ambulance behind you as the ambulance approaches you. What is the change in sound frequency after it passes you?

1. Determine the speed of both the ambulance and the bicycle. Let's assume that the ambulance travels at 60 km/h and the bike at 15 km/h.

2. Determine the sound frequency. Let's take 700 Hz.

3. Decide on the signs of both velocities before the ambulance passes you: are they negative or positive? Ambulance velocity will be negative (as it moves towards you), and the bicycle velocity will be negative as well (because you move away from the source).

4. Calculate the observed frequency of sound before the ambulance moves past you using the Doppler shift formula. You can check in our Doppler effect calculator that the result will be equal to 727 Hz.

5. Decide on the signs of both velocities after the ambulance passes you. Ambulance velocity will be positive (as it now moves away from you), and the bicycle velocity will be positive as well (because you move towards the source).

6. Calculate the observed frequency of sound after the ambulance moves past you. The result will be equal to 676 Hz.

7. Finally, subtract one value from the other to find the change in frequency: 727 - 676 = 51 Hz.

If you are interested in sound Physics, also try the dB calculator.