dB Calculator

This dB calculator will help you find the sound pressure level (SPL) and intensity level in decibels. You can use it for dB conversion or for determining the distance from the source of a sound.

If you need a refresher on sound waves, look at our sound wavelength calculator.

When we hear a very loud noise, we experience unpleasant feelings. It is because of the pressure of a sound wave. The sound pressure level, or SPL, is simply the measure of sound pressure with reference to the human hearing threshold. Even though this pressure can be measured in Pascals, like air pressure, it is more practical to use decibels - a logarithmic unit.

The formula for the sound pressure level is:

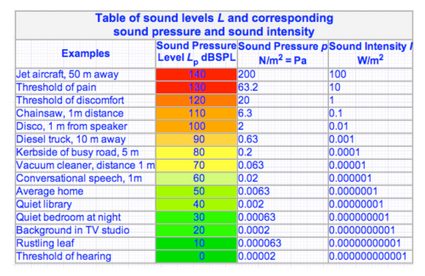
SPL = 20 × log(P/Pref)

where:

• SPL — Sound pressure level in dB;
• P — Sound wave pressure, measured in pascals; and
• Pref — Reference value of sound pressure. Typically, it is assumed to be equal to 0.00002 Pa.

As you probably noticed, the SPL increases logarithmically. Also, it is a relative measure, while the regular sound wave pressure is an absolute measure of loudness.

Sound intensity level (SIL) is defined as the sound wave power per unit area. This quantity allows us to measure the energy of sound (or, to be more precise, the energy per second per one squared meter). The formula is:

SIL = 10 × log(I/Iref)

where:

• SIL — Sound intensity level in dB;
• I — Sound intensity in watts per squared meter; and
• Iref — Reference value if sound intensity. Typically, it is assumed to be equal to 1×10⁻¹² W/m².

Sound intensity changes with the distance from the sound source. It's just common sense — if a car passes you, you hear a loud noise that gets quieter as the car moves away. Our distance attenuation calculator determines this distance-sound intensity relationship.

From a physical point of view, it happens because the energy of sound is now distributed over a larger area. Imagine a sphere surrounding the sound source. Even though the energy emitted by the source is constant, the sphere can get larger - its surface will increase. The energy will be distributed over the area of the sphere. Not surprisingly, we can write it down in the form of an equation:

I = P/(4πR²)

where:

• I — Sound intensity;
• P — Power of the sound source; and
• R — Radius of the sphere, i.e., the distance from the sound source.

The attenuation of power radiated by a source with an increase in distance is a characteristic of all electromagnetic radiations, and we study it in the free space path loss calculator.

For different materials, the intensity and pressure of the sound are also affected. In our acoustic impedance calculator, you can learn how the medium affects those variables.

Our decibel calculator can be used to find the equivalent of sound wave pressure in decibels. Simply type the pressure in pascals into the dB calculator to find the sound pressure level. You can also use this tool in reverse to find the pressure if SPL is given.

If you're interested in acoustics, make sure to take a look at the reverberation time calculator, too!