Flat vs. Round Earth Calculator
What is the best way to learn about the world? Propose a theory and set out to prove it with observations (science)? Or just make stuff up and ignore obvious facts (nonsense)? Here at Omni, we tend to think the first option is doing pretty well. It got us to the Moon, didn't it? – It really did, by the way.
To celebrate World Science Day for Peace and Development, held every 10 November, we've created a calculator that helps you fight against bunkum, half-truths and baloney, and for science, observation, and open-mindedness.
Omni's flat vs. round Earth calculator features experiments that help prove that the Earth is indeed round. Don't worry; you won't be building your own rocket to go into outer space to check (or calculate its impulse and momentum or its kinetic energy).
We have three relatively simple experiments for you to try:
-
Sunset twice — By changing your viewpoint above the ground, you can see a sunset twice. Our calculator tells you how much of the second sunset you will see.
-
Disappearing objects — Hide objects behind the curvature of the Earth by changing the height of your viewpoint. This calculator will show you how tall an object you can make disappear.
-
Stick shadows — Use the lengths of shadows cast by a stick at different locations to estimate the circumference of the Earth.
Before we get to the experiments, let's briefly overview why people might believe in a flat Earth and the model of the world they put forward.
Belief in a flat Earth
Amazingly, in the richest, most technologically developed country in the world, are not sure if the Earth is round 🤔. Of course, the country is the USA, and belief in a flat Earth may stem from its highly individualistic culture and a distrust of authority, institutions, and experts.
Flat Earthers seem to look at the world all on their own, without reference to the well over 2,000 years of human discovery. Wow, they are missing out. They are also extremely distrustful of any facts that they haven't verified for themselves personally. Talk about trust issues.
They then take on extraordinary challenges to prove the Earth is flat when there are simple things they could do to prove the Earth is round. Here are some examples:
- built his own steam-powered rockets to fly to a height of 1,800 feet (550 m) to photograph the lack of curvature of the Mojave Desert. Unfortunately, you need to go up to at least 35,000 feet (11,000 m) to see the curvature of the Earth. He sadly passed away in February 2020 in a failed rocket flight.
- YouTube star to find the edge of a flat Earth. However, the trip did not occur due to the COVID-19 pandemic and the lack of medical facilities to support any emergencies.
- to check for a flat Earth. He only managed to raise $6,883 of his $1 million goal. Oh well, never mind. Maybe he could try out our simple, low-cost experiments instead.
This cartoon by Tom Fonder sums up flat Earthers quite nicely.

The flat Earth model
In the flat Earth model, the world is a disk (similar to the gears used for gear reduction) with the north pole at the center. Around the edge of the disk is the ice and snow of the "south pole." This then forms an icy barrier, presumably to stop the water of the oceans from falling off of the disc into space.

The thickness of the flat Earth disk is not clear. However, the mass involved must be much less than a round Earth, so Earth wouldn't be able to hold on to its atmosphere. Maybe there is a transparent dome over the Earth, stopping it from escaping.
The traditional flat Earth model has the sun positioned over the disk, circling around in the sky like a baby's mobile and at a much closer distance. That then doesn't explain sunsets and sunrises. For some sanity, let's imagine the disk spins like a coin relative to the sun. That would at least get our sunrise and sunset back (something the simplest animal could observe). However, there would be no timezones as sunrise and sunset would be at the same time all over the world.
🔎 💻 You can experience what it's like to live on a flat Earth using a created by Bruce Sherwood. It shows the sun never setting and its apparent size changing throughout the day, plus many other things we simply don't observe in reality.
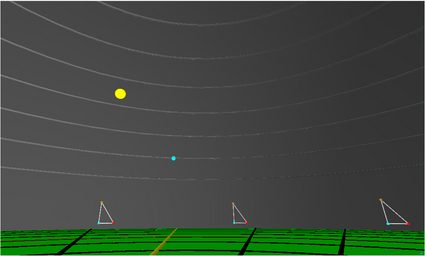
That's the main problem with the flat Earth model. It's full of inconsistencies and unexplained observations. For example, why is it cold at both the center and the edge of the disk?
Let's get back to a more scientific way of thinking and introduce the first experiment.
Sunset twice experiment
This first experiment can be really simple to perform. Move upwards quick enough to get ahead of the shadow cast by the horizon. You’ll then be able to see part of the sunset twice! If you observe this, then the Earth is indeed round. This experiment will calculate how much of a second sunset you could see and how long you could make a sunset last.
What would you see if the Earth was flat? No second sunset 😭. No matter how high or fast you traveled up from the surface of a flat Earth; you wouldn't see the sun again until dawn.
For a round Earth, as the sun sets, imagine the shadow cast by the Earth's horizon coming towards you and moving up your body. If you can get ahead of this shadow by moving upwards fast enough, you can see the sunset again. Let's take a look at the math.
This gives us an equation that relates time with the height of the shadow:
t = 8 × √h,
where t is the time it takes the shadow to move up in height by the amount h. We can relate h to the height difference between two heights and t to the time it takes to move upwards. Because we can't instantly travel from the lower to the higher height, we need to consider the travel time. Finally, to find the amount of a second sunset we can see again, we need to know the sunset duration. We then have this equation for the percentage of the sunset two you will observe again:
Sunset two percentage = 100 × (1 - ((Sunset duration - t - Travel time) / Sunset duration))
Directions to see a sunset twice
There are a few ways to see the sun again just after it has set, to varying degrees. Omni's flat vs. round Earth calculator will tell you how much of a second sunset you will be able to observe. Let's go through three ideas we've come up with.
1. Lie down, stand up
This idea is the simplest in terms of equipment. You just need a location where you can see the sun setting into the sea or very flat land (like a desert). A beautiful cloudless sky will also help. All you need to do is watch the sunset while lying down. Once you can't see any of the Sun anymore, immediately stand up as fast as you can. You should be able to see a small part of the top of the sun again.
Here's how to use the calculator to compute precisely how much.
- Select a location closest to you or manually enter the sunset duration where you are.
- Enter the lower starting height of your eye-level. In this case, when lying down. We recommend about 8 inches (20 cm).
- Input how long it will take you to get to the higher height. We reckon about half a second but do go ahead and time yourself to double-check.
- Enter the final height of your eye-level when you are standing up. You can measure this by subtracting the distance from the top of your head to your eyes away from your height.
- You will then see the percentage of the sun you'll be able to see set again. Want to see more? Try changing the values in the calculator or go to the more advanced variations of the experiment below.
You should be able to see around 5% of the second sunset with this method.
2. Fast lift up a skyscraper
To see more of the second sunset, you're going to have to go higher and faster to get ahead of the horizon's shadow. A skyscraper with a fast lift is one option. This phenomenon has been at the Burj Khalifa hotel in Dubai.
To select the input values for this skyscraper, choose "Sky scrapper lift – Burj Khalifa hotel" from the ideas list. If you want to try this at another building, adjust the input values accordingly.
You should be able to see a massive 88% of the sunset again, and so nearly doubling the duration. If you are a sunset lover, this is the thing to do.
3. Drone with a camera
Another idea is to use a good-quality drone that has a live streaming camera capability. We found one drone that can reach 3,300 feet (1,000 m) in 200 seconds. If you select "Drone" from the list of ideas, you'll see that you should see about a third of the sunset again with this method.
Check how fast and high your drone can go and adjust the values in the calculator accordingly.
Disappearing object experiment
In this experiment, we will hide part of an object behind the curvature of the Earth. You will need to find a body of water where the far shore is at least a mile and a quarter away (2 km), and it needs to be a nice calm day with no wind.
Also, to help avoid the mirage effect (light refraction), do the experiment in the morning when it's cool. That's also why we don't recommend using a desert – the mirage effect will mean you won't be able to see objects on the far shore clearly enough.
In this YouTube video, the guy made a truck 4 miles (7 km) away disappear on the far side of a lake by lowering his camera closer to the ground.
Alternatively, an off-shore wind farm is also a good option, as this photograph demonstrates:

Notice the further away a windmill is, the more of it is hidden. That's what this experiment is about – calculating how much of a distant object you can hide behind the curvature of the Earth.
💡 The curvature of the Earth has been measured as 8 inches per mile (12 cm per kilometer). That means that for every mile you are away from an object, 8 inches of the bottom of the object is hidden by the curvature of the Earth. However, that does assume you are looking at the object a zero height, which is not very practical.

In this experiment, we will start at a high viewpoint and then go down to a low viewpoint to obscure a distant object. In math terms, we find how much is hidden at the high and low views and calculate the difference.
To calculate the obscured height, we first need to know the distance to the horizon. This is given by this equation:
a = √[(r + h)² - r²]
where:
- a is the distance to the horizon,
- h is viewpoint level above the ground, and
- r is the Earth's radius, equal to 3,959 miles or 6,371 km.
Then we input the result into a second equation that calculates how much of the object is obscured, x, if viewed from zero height:
x = √(a² - 2ad + d² + r²) - r
The difference in the two values of x is the height of the object we can make disappear by changing our viewpoint.
Instructions for hiding an object behind the curvature of the Earth
OK, so you've found an excellent location, such as a lake with shores a few miles apart. To see any objects on the far shore, you will need some good binoculars. Better still, a video camera with a powerful zoom lens. That would also allow you to record the experiment, just like in the video above.
To get a steady view through your binoculars or camera, mounting them on a tripod is recommended. Using a tripod also allows you to measure the two heights accurately.
Here is how to use the calculator to figure out what size object you might be able to disappear behind the curvature of the Earth.
- Measure the distance to the far shore of the lake. You can use a paper map or the measuring feature on Google Maps to do this. Input the distance into the "Distance to object" variable in the calculator.
- Measure the height above the ground of your eye-level while standing up or your camera when it is in the high height position. Enter this height in the next input field.
- Do the same when you are lying down, or your camera is in the low height position. To maximize the effect, try to get as low to the water level as possible.
- You'll then see the height of an object that is obscured by the Earth’s curvature is calculated for you. If it seems too small to see, try increasing your high height and decreasing your low height.
If the Earth is flat, you wouldn't see any difference in the objects on the far side of the lake, no matter how low to the ground you view them.
Stick shadow experiment
This experiment not only proves the Earth is round, you can also estimate the circumference of the Earth. This is precisely what Greek mathematician Eratosthenes did in Alexandria, in around 240 BC. He knew that in Aswan, around 500 miles to the south, there was a well where sunlight reached the bottom at noon on the summer solstice. At the same time, he measured the shadow cast by a stick in Alexandria.
Assuming the Earth is round and the sun is far away, and using the mathematics we'll go through below, he concluded that the Earth's circumference was about 50 times the distance between Alexandria and Aswan. That is within 10% of the correct answer. A fantastic result for such a simple experiment performed over 2,000 years ago.
💡 Earth's circumference is the distance around the Earth. Measuring around the poles it's 24,860 miles (40,008 km). Measuring around the equator it's 24,901 miles (40,075 km). The slight difference between the two measurement is because the Earth spins.

Looking at the triangle formed by the stick and the shadow, we can use the inverse tangent trigonometry function to calculate the angle between the stick and the sunlight ray, using the equation:
θ = arctan(Shadow length / Stick height)
So we do that for the two locations. How do these two angles relate to the circumference of the Earth? The figure below will help us to answer this question.

Using some geometry, we can show that the angle α between lines that go through locations A and B, and the center of the Earth, is the difference in the stick shadow angles:
α = θ₂ - θ₁
We now know the arc length (distance along the surface of the Earth) between A and B, and the angle α. This allows us to simply scale up the distance to the full Earth circumference, using the equation:
Earth circumference = Distance A → B × (360° / α)
It's important to note that the distance from A to B should be the distance if you could only travel north or south (the north-south distance). We need this distance as it is only when you travel northwards does the shadow cast by the stick gets longer.
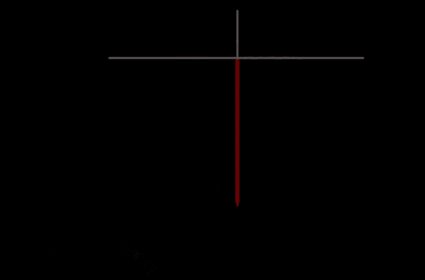
Assuming point A is south of point B, on a map, draw a line due north from point A. Then draw a line due east from point B. The north-south distance is the length from point A to where the two lines you drew cross over each other.
Instructions for measuring how big the Earth is using stick shadows
There are two main ways you can try this experiment. You can either travel a considerable distance north or south (greater than 100 miles, but the further, the better) or partner up with someone who lives far away to help you.
Let's start with the traveling option. It's best to attempt this around the shortest or longest day of the year, as the day length is relatively stable. That will reduce errors in the shadow angle measured at the two locations. Here are step-by-step instructions:
- Measure the length of your stick. You'll need to enter this into the first input field of the calculator. If part of the stick is in the ground, only include the length above the ground.
- Measure the length of the shadow at location A at local noon time. If it's not a sunny day, wait until you get one. Input the shadow length into the calculator, and the shadow angle will be calculated for you.
- Travel to location B and do the same as in step 2.
- Using a map, measure the north-south distance between the two locations and enter this figure into the calculator (see instructions above).
- You'll then receive an answer to your measured estimate of the Earth's circumference and how close you got to the real answer.
If you have a friend at another location to help you, that's even better! The experiment will be the most accurate if you do both measurements on the same day of the year and at the same solar time. In this case, the steps are basically the same. Make sure the two sticks are the same length and that you measure the shadow at noon local time on the same day. This option is a lot easier and can be performed on any sunny day of the year.
Example calculation of a stick shadow experiment
For an example, let's travel north from Florida to Pennsylvania (A to B), covering a north-south distance of around 1,000 miles (1,609 km). The stick is 3 feet (0.91 m) long, and we measure a shadow length of 3 feet at A. That means a shadow angle of 45°. We then travel to B and measure a shadow of 5.2 feet, which means the shadow angle here is about 60°.
Enter all these figures into the calculator, and we get a result of 23,971 miles (38,577 km). That's within 4% of the real circumference as measured between the poles of 24,860 miles (40,008 km).
What happens in the stick shadow experiment if the Earth is flat?
Let's imagine that the flat-earthers are right for a moment. How does the above example work in a flat Earth model?
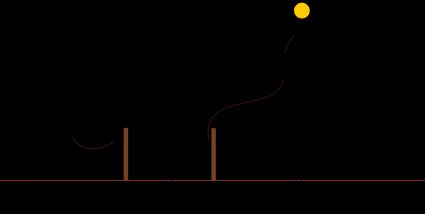
In a flat earth model, sticks will still cast a shadow of different lengths. However, the result of doing some trigonometry leads to a strange result. Referring to the above diagram and applying said trigonometry, we can say that:
d = h × |tan θ₂ - tan θ₁|
Using the angles 45° and 60°, and 1,000 miles for d, we see that the distance to the sun h is
h = 1,000 / (1.73 - 1) = 1,370 miles
That does seem very close. However, the flat earth model can say the sun is much smaller than science has concluded.
Now we can calculate the two other distances to the sun from the two locations:
R₁ = h / cos θ₁ = 1370 / cos(45°) = 1937 miles
R₂ = h / cos θ₂ = 1370 / cos(60°) = 2740 miles
This result means that by traveling south 1,000 miles, the sun should have got smaller by around 40%. In reality, as you can verify for yourself, the sun does not appear to get smaller as you travel southwards.
Therefore, we can conclude that the flat Earth model is wrong. It does not agree with observation. That is the crucial property of any scientific model. It must agree with experimental results.
FAQs
When did we learn that the Earth is round?
The notion that the Earth is spherical is quite old! In Ancient Greece, scientists and philosophers were aware of this fact as early as the V century B.C.
Even in later centuries, the spherical model was more widely accepted and only marginally questioned outside purely mythological grounds: this theory's apparent resurgence and relevance in modern times is purely a consequence of the change in our communication methods.
How do I calculate the circumference of the Earth using shadows?
To calculate the circumference of the Earth using shadows:
- Ask a friend living at a different latitude to perform the same steps as you; then:
- Vertically plant a stick of known length in the ground.
- Measure the angle between the stick and the sun rays at a given time of the local day.
- Use the formula:
θ = arctan(Shadow length / Stick height). - Now use this formula for Earth's circumference:
Earth circumference = Distance × (360° / α),
where:Distanceis the north-south distance between the sticks; andαis the difference between the angles calculated before.
How high should I be to see the curvature of Earth?
To see the curvature of the Earth, you must be at an altitude of around 35,000 ft or 10.5 km. This is about the cruising altitude of a passenger plane. However, to see it properly, you need a completely clear horizon (no clouds) and a field of view of at least 60 degrees. Both these conditions are rarely satisfied from the windows of your plane, but you can try.
Also, notice that the curvature is not visible even from the summit of Mt. Everest!
How can I prove that the Earth is round?
To prove that the Earth is round, go to the beach! If there is a long enough stretch of sea in front of you, you can simply wait for a ship to approach the coast. You will first see its top part appearing above the horizon, slowly followed by the rest of the ship.
As the Earth is round, its curvature covers part of the ship. The covered part gets smaller as the ship approaches you.
Now, the hard part is to convince skeptics that this is a definitive answer!
