Gear Ratio Calculator
This gear ratio calculator determines the mechanical advantage a two-gear setup produces in a machine. The gear ratio gives us an idea of how much an output gear is sped up or slowed down or how much torque is lost or gained in a system. We equipped this calculator with the gear ratio equation and the gear reduction equation so you can quickly determine the gear ratio of your gears.
Keep on reading to learn more about gear ratio calculation and how it is essential in making simple machines (and even complicated ones).
Prefer watching rather than reading? Learn all you need in 90 seconds with this video we made for you:
What is a gear?
A gear is a toothed wheel that can change the direction, torque, and speed of rotational movement applied to it. Gears come in different shapes and sizes (even if the most common are involute gears – see involute function calculator), and these differences describe the translation or transfer of the rotational movement. The transfer of movement happens when two or more gears in a system mesh together while in motion. We call this system of gears a gear train.
In a gear train, turning one gear also turns the other gears. The gear that initially receives the turning force, either from a powered motor or just by hand (or foot in the case of a bike), is called the input gear. We can also call it the driving gear since it initiates the movement of all the other gears in the gear train. The final gear that the input gear influences is known as the output gear. In a two-gear system, we can call these gears the driving gear and the driven gear, respectively.
The resulting movement of the output gear could be in the same direction as the input gear, but it could be in a different direction or axes of rotation depending on the type of gear in the gear train. To help you visualize this, here is an illustration of the different types of gears and their input-to-output gear relationships:
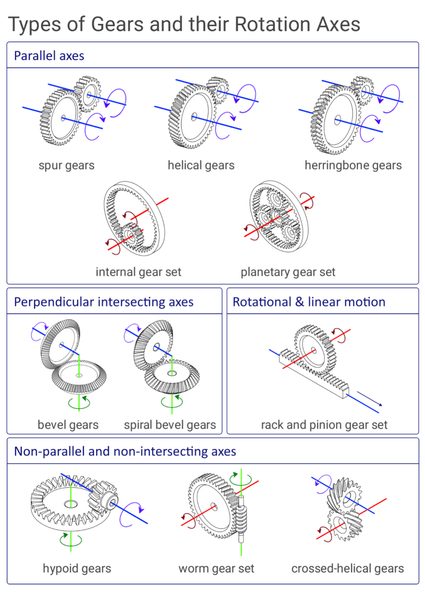
You might also like our chain length calculator and speedometer gear calculator.
What is gear ratio and how to calculate gear ratio
The gear ratio is the ratio of the circumference of the output gear to the circumference of the input gear in a gear train. The gear ratio helps us determine the number of teeth each gear needs to produce a desired output speed/angular velocity, or torque (see torque calculator).
We calculate the gear ratio between two gears by dividing the circumference of the output gear by the circumference of the input gear. We can determine the circumference of a specific gear in the same way we calculate the circumference of a circle. In equation form, it looks like this:
gear ratio = (π × diameter of output gear)/(π × diameter of input gear)
Simplifying this equation, we can also obtain the gear ratio when just the gears' diameters or radii are considered:
gear ratio = (diameter of output gear)/(diameter of input gear)
gear ratio = (radius of output gear)/(radius of input gear)
Similarly, we can calculate the gear ratio by considering the number of teeth on the output and input gears. Doing so is similar to considering the circumferences of the gears. We can express the gear's circumference by multiplying the sum of a tooth's thickness and the spacing between teeth by the number of teeth the gear has:
gear ratio = (output gear teeth number × (gear thickness + teeth spacing)) / (input gear teeth number × (gear thickness + teeth spacing))
But, since the thickness and spacing of the gear train's teeth must be the same for the gears to engage smoothly, we can cancel out the gear thickness and teeth spacing multiplier in the above equation, leaving us with the equation below:
gear ratio = output gear teeth number / input gear teeth number
The gear ratio, just like any other ratio, can be expressed as:
-
A fraction or a quotient – where, if possible, we simplify the fraction by dividing both the numerator and the denominator by their greatest common factor.
-
A decimal number – expressing the gear ratio as a decimal number gives us a quick idea about how much the input gear has to be turned for the output gear to complete one full revolution.
-
An ordered pair of numbers separated by a colon, such as 2:5 or 1:14. With this, we can see the fewest number of turns required for both the input and output gears to return to their original positions at the same time.
From a different perspective, we can say that the gear ratio also expresses the amount of mechanical advantage (or disadvantage) our gear train or gear system has.
Understanding gear ratio and mechanical advantage values
Gear ratios are pretty easy to understand, and now that we know how to calculate a gear ratio, wouldn't it be better to know how it affects the gears themselves? To better explain gear ratios, let us consider a two-gear system where the input and output gears have ten and forty teeth, respectively:
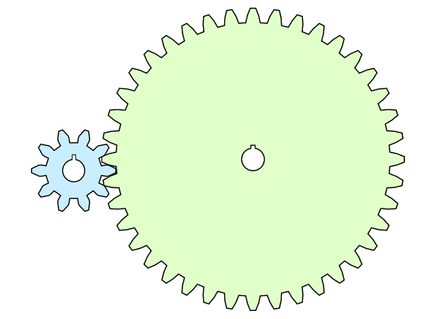
Following our gear ratio equation, we can say that this gear train has a gear ratio of 40:10, 40/10, or simply 4/1 (or 4). This gear ratio means that the input gear would need to rotate 4 full turns for the output gear to complete one full rotation. Continuing in this fashion and keeping a consistent input speed, we see that the rate of the output gear is also 1/4 of that of the input speed. In other words, the speed of the input gear is four times the speed of the output gear, as can be seen in the animated image below:
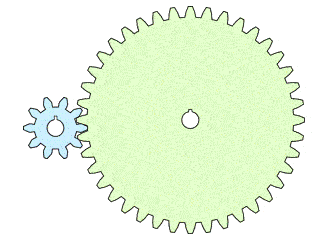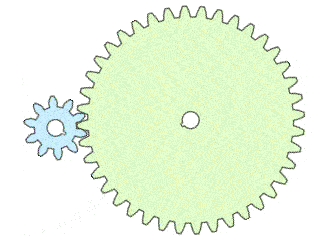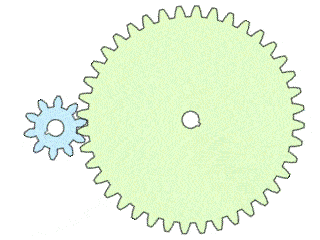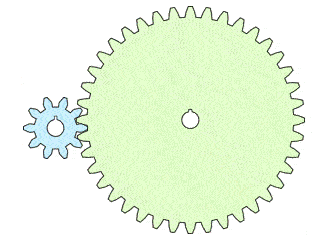
While this setup demonstrates a gear reduction in terms of speed, in return it provides us with an output that has more torque, when compared to the input. With a gear ratio of 4, we can say that we get four times the mechanical advantage when it comes to torque.
Important note on idler gears
A spur gear of any number of teeth between the input and output gears does not change the total gear ratio of the gear train. However, this gear (or gears) can change the direction of the output gear. We call this in-between gear an idler gear. As an example, here is a 2.5:1 gear reduction system with an additional idler gear:
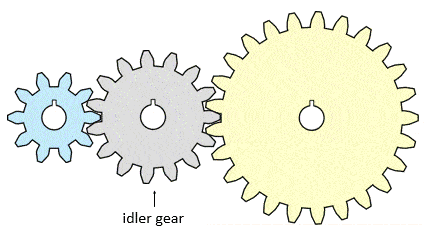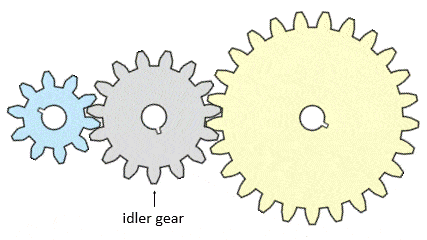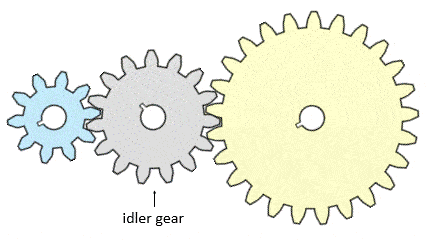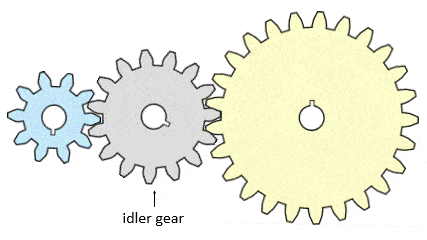
Without the idler gear, here is the same gear train. Note that the direction of the output gear is reversed:
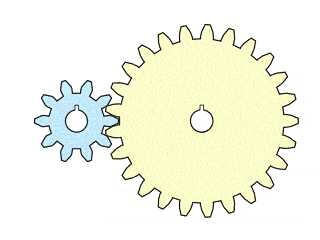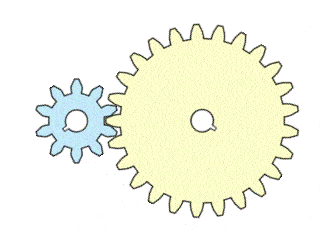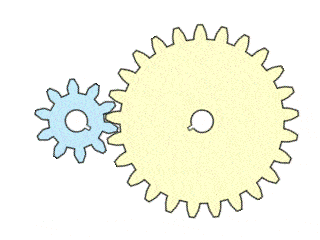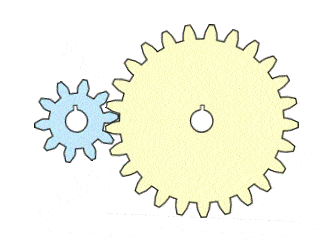
Real-life simple machines with gears
We see gears in our everyday lives, and to gain an even better understanding of gear ratios, here are some real-life examples of simple machines with gears in them:
Mechanical advantage in terms of speed

Hand drills, though they seem less popular nowadays, are a great example of a simple machine that demonstrates a mechanical advantage in terms of speed. Cranking its handle will spin the drill bit at high speed.
Mechanical advantage in terms of torque

Going uphill, riding a bike is easier if you are in a low-speed gear. Doing so results in better torque, providing more power when going uphill. This may mean we have to pedal more, but our ascend will be much easier. A bicycle sprocket-and-chain mechanism is much like a rack-and-pinion setup. The chain acts as a rack gear, directly transferring the motion to the rear bike sprocket (see the bike gear calculator).
FAQs
What is a gear?
A gear is a circular machine part that transmits torque when it meshes with its counterpart. Gears are usually a vital part of any machine with moving parts, such as a wristwatch or an automobile.
What are different types of gears?
There are different types of gear depending upon the angle of power transmission. For parallel transmission, these include spur, helical, herringbone, and planetary gears. Bevel and spiral bevel gears are used for perpendicular transmission.
What is the gear ratio?
Gear ratio is defined as the ratio of the circumference of two gears that mesh together for power transmission. This parameter determines whether the amount of power transmission will increase or decrease.
How do you calculate gear ratio?
To calculate the gear ratio:
-
Find the 1st (driving) gear's number of teeth or diameter.
-
Find the 2nd (driven) gear's number of teeth or diameter.
-
Divide the number of the driven gear by that of the driving gear to find the gear ratio.
Alternatively, you can also find the gear ratio by dividing the speed of the 1st gear by the 2nd gear.