Involute Function Calculator

Not happy with simple curves, mathematicians decided to see what happens when two curves slide on one another, and the result made many engineers extremely happy: discover why with our involute function calculator!

Here you will learn:

• What the involute function is;
• What it has to do with involute curves; and
• How it is related to the gear pressure angle, which is a very important concept in engineering. ⚙️

When mathematicians talk about roulette, they are not talking of the casino game but rather of a particular family of curves obtained by rolling a curve on another fixed curve and following the trajectory of a given, fixed point integral with the rolling curve. The other conditions are that:

• Both curves must be differentiable — this means that it is "smooth" in its entirety, without points like cusps or interruptions where it would be impossible to define its slope.
• The curves must be tangent at every moment.

A particular class of roulette curves is obtained by following a line wrapped around a curve (taut string) as it unwraps, or vice-versa: this type of roulette is called the involute.

When we talk of a string wrapped around a circle, the resulting curve, resembling a spiral, is called the involute of a circle. Here it is, with its construction.

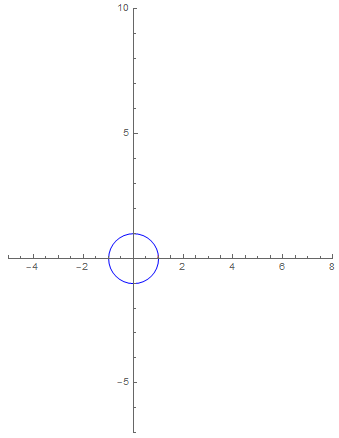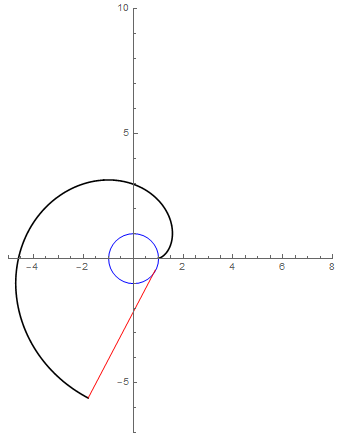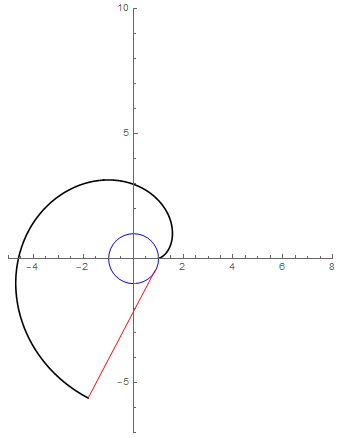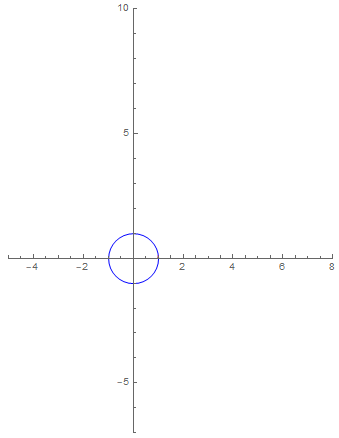
The red straight line represents the tensioned string as it wraps/unwraps. The tip of the string draws the involute.

The involute is described by this parametric equation:

where $a$ is the radius of the circle and $\theta$ is the angle at which the string separates from the circle (where circle and line are tangent).

Involute functions are interesting for mathematicians but fundamental for engineers: the main application of the involute function is the construction of involute gears.

It is necessary to introduce a few elements of involute gears:

• The line of action and the line of centers;
• The pitch point;
• The pressure angle.

The line of centers connects the centers of the two gears. While a couple of teeth are in contact as the gears roll, the point of contact moves along an imaginary line called line of action.

This is the core point of the peculiarity of involute gears: the contact between teeth happens only on a straight line — obviously, if the teeth' profiles match.

The pitch point is the point on the line of centers where the circumferential speeds of the gears (you can learn how to calculate it with the circular motion calculator) match: this means that points on gears' edges travel at the same speed. In involute gears, this is also the point of intersection between the action line and the line of centers.

Let's draw the perpendicular to the line of centers passing through the pitch point.

At this point, the angle between this line and the action line is called the pressure angle. Its value remains constant during the operation of the gears; hence, it is characteristic of a given design.

The involute gear pressure angle is the fundamental parameter when designing the gear itself, since its value affects the tilting of the line of action and the behavior of the gear during its operations.

Here is how to calculate the involute as a function of the pressure angle.

We start by building the circle with center $O$ and radius $OS$. Then, we draw a part of the involute of the circle. We call the origin point $S$, then choose a point $P$ on this curve. The taut string touches the circumference in the point $T$.

By construction, the segment $TP$ and the arc $ST$ have the same length. It is then possible to write: $\overline{TP} =\stackrel{\frown}{ST}$.

In this construction, the angle of pressure is the angle $\hat{TOP} = \alpha$. The other angle, $\hat{SOP} = \varphi$, can be found following the next steps:

The last expression is the involute function $\tan$ is the tangent function. The resulting angle is extremely important in the design of involute gears, for example, in the calculation of the tooth thickness.

From the geometrical construction, you can see that $\varphi$ (the value of the involute function for a given pressure angle $\alpha$) is somehow connected to the "thickness" of the tooth of an involute gear. This explains why the involute function is so important.

An increase in the pressure angle equals an increase in the width of the tooth. A wider tooth is a stronger tooth that can withstand bigger loads. On the other hand, smaller teeth obtained by reducing the pressure angle $\alpha$ give advantages to the smoothness of the operation.

Using our involute function calculator is really easy. You can input the value of the gear pressure angle $\alpha$ to obtain right away the value of the relative involute function.

Let's try with an example.

The most common gear pressure angle currently used is $20\degree$. In the involute function calculator, change the units of $\alpha$ to degrees and input $20$. The result is dimensionless and equal to $\thicksim 0.0149$.

If you are interested in other calculators, check our gear ratio calculator, the gear ratio speed calculator, or discover the sister curve of the involute with the catenary curve calculator!