Laser Beam Expander Calculator

Our laser beam expander calculator allows you to compute the effects of a beam expander on your beam, the consequences and the advantages of using such devices, and more. Keep reading to learn:

• What a laser beam expander is, and what are the laser beam expander designs?
• How to calculate a laser beam expander's magnification.
• The effect of the expander on beam size and divergence.
• How to calculate the size of the beam at a given distance from the expander.

Let's shine some light on the topic!

Lasers are known for their small and focused beam sizes. What if that is, in fact, a nuisance in your applications? A small beam spot size can easily focus too much power on a reduced surface, damaging optics or coatings, or in other applications (for example, defense) where it's required to point at distant objects. Also, a small beam size would require meticulous targeting.

A laser beam expander takes a beam with a small size, entering with light rays parallel to the optical axis of the device, and expands it by a factor controlled by the fabrication parameters, giving in output a larger beam, with rays still parallels to the optical axis.

What happens inside a laser beam expander?

The design of a laser beam expander

The fundamental elements of a laser beam expander are lenses! Depending on the type of lenses, we can identify two designs of laser beam expanders:

• The Galilean beam expander; and
• Keplerian beam expander.

The Keplerian beam expander uses lenses with positive focal lengths assembled so that we can find a focus point inside the body of the expander.

The Galilean beam expander uses a lens with a positive focal length and a lens with a negative focal length. During our calculations, we will take the absolute value of the negative focal length: we are only interested in the behavior (it focuses a non-parallel beam).

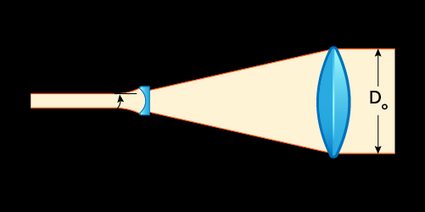
In both cases, the lenses are placed at a distance equal to the sum of their focal lengths, which implies that a Galilean beam expander is much shorter than an equivalent Keplerian beam expander.

What are the advantages and disadvantages of these designs? Thanks to the focus point in their bodies, Keplerian beam expanders allow you to "clean" the beam and also offer high expansion ratios. On the other hand, however, focusing the beam on a point causes the medium to heat up, possibly damaging the device or compromising its optical qualities.

For this reason, the Keplerian laser beam expander design is often relegated for pulsed lasers, where there is no time to heat the medium. Galilean beam expanders are smaller and, thanks to the absence of a focus spot, are often used in power applications where continuous, high-energy beams are employed.

Even though we can find two designs for a laser beam expander, the calculations don't differ at all! Let's dive into the math of these devices.

The first thing we can compute right away is the magnifying power of the laser beam expander: the lenses' focal lengths are the only quantities we need to know:

where:

• $f_\mathrm{O}$ — Focal length of the objective lens, the one corresponding to the expanded, output beam; and
• $f_\mathrm{I}$ — Focal length of the image lens, the one where you shine your beam onto.

The magnifying power is an immediate quantity to understand, as it assumes values corresponding to how much our beam will expand (it's what we commonly call "zoom"). However, in optics, we often deal with the magnification, a slightly different concept. In a laser beam expander, we calculate the magnification as the multiplicative inverse of the magnifying power:

Our telescope magnification calculator can help you wrap your head around how objects grow in apparent size even though the magnification can be a value much smaller than $1$.

Once you know the magnification and magnification power, you can compute how the laser beam expander affects your beam. We will deal with two quantities:

• The laser beam spot size; and
• The laser beam divergence.

While the first quantity is straightforward to understand (though its definition depends on the properties of the beam), the divergence requires a bit more understanding. Even though laser light is highly collimated, a degree of spread of the rays is always present. This causes the beam to open up and eventually dissipate. Laser beams' divergence is a complex quantity that depends on many fabrication factors, including the wavelength of the light emitted.

We are not surprised to learn how a laser beam expander affects the size of the laser beam. To compute the final diameter at the exit lens of a device, we use the following equation:

where $D_\mathrm{O}$ and $D_\mathrm{I}$ are the laser beam spot sizes at, respectively, the objective and the image lenses. In any reasonable laser beam expander design, the magnifying power is a large positive number, which causes $D_\mathrm{O}$ to be much larger than the initial value.

When it comes to the divergence, we find a similar formula, but the order of the lenses is "inverted":

With the same value of magnifying power as before, we now notice that the divergence is reduced by the action of a laser beam expander. While this is not much of a problem when expanding a laser beam, it may be annoying when using the laser beam expander to shrink the beam size. In this case, the divergence would increase, reducing the quality of the beam at relatively large distances.

By knowing the parameters of your optical set-up, you can compute the laser beam diameter at any given distance from the laser beam expander. Use the following formula:

where $L$ is the desired distance from the beam expander, and $D_\mathrm{L}$ the corresponding beam size.

Our laser beam expander calculator is straightforward to use. You can calculate either the magnification, the final diameter or divergence, or the diameter at a distance, or all together: it depends on the values you input.

Let's try some real-life values. We chose two lenses for a Galielan system:

• The image lens with negative focal length $f_\mathrm{I} = - 25\ \mathrm{mm}$; and
• The objective lens with focal length $f_\mathrm{O}= 150\ \mathrm{mm}$.

We take the absolute value of the focal length of the first lens and calculate the magnifying power as:

We commonly write this result as $\mathrm{MP}=6\mathrm{X}$.

If you shine a beam with diameter $D_\mathrm{I} = 2\ \mathrm{mm}$ on the image lens, you can compute the output diameter of the beam with the following formula:

If the initial divergence is relatively small at $0.4\ \mathrm{mrad}$, we can find the final divergence simply by dividing this value by the magnifying power:

How big will the spot be at the other end of the room, say, at a distance $L =5\ \mathrm{m}$?