Telescope Magnification Calculator

This is the telescope magnification calculator, a great tool that helps you set your scope for both amateur and professional astronomical observations. In the article below, you can find the answer to the question: How does a telescope work? as well as learn about the magnification equation of a scope.

What's more, you'll find not only how to calculate magnification but some other interesting image properties to look for. Get ready, and be well prepared for your next stargazing activity!

You must have seen a lot of beautiful pictures of galaxies, nebulae, and planets taken by both huge, high-powered telescopes and small, home-used ones. Have you wondered how it's possible to see such distant objects and scale up their images to see that much detail smoothly? Here is how it works:

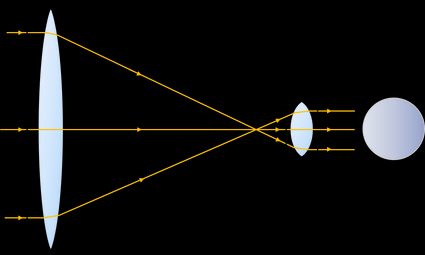
A telescope consists of two main elements, an objective and an eyepiece. The objective is usually a mirror, or a lens, that focuses the incoming light of the observed object. The eyepiece is a set of lenses that corrects the direction of the beam and lets you get closer to the image. Learn more about how the eyepiece affects your skywatching experience with our telescope field of view calculator.

The second thing is that the objective collects the light from its whole surface (also known as the aperture) and processes it through the much smaller surface of the eyepiece. The same amount of light enters and exits the telescope, so the image is not only magnified but also has its brightness increases significantly! This effect is amplified in the highest-powered telescopes, which is why they are able to detect exoplanets.

As we know the general concept of how a telescope works, we can take a step further and ask: How to calculate magnification?

We've mentioned the objective and the eyepiece above. Focal lengths or focal diameters can characterize both. The magnification equation of a telescope is then:

M = f_o/ f_e,

where:

• M is the magnification of the image;
• f_o is the focal length of the objective (sometimes referred to the telescope focal length); and
• f_e is the eyepiece's focal length.

As you can see, the magnification of the telescope gets greater when the focal length of the objective increases or when the eyepiece's focal length decreases.

The focal length of the objective usually goes hand in hand with the length of the telescope itself. That's the reason why the highest-powered telescopes are such monsters with huge mirrors. The biggest ones are actually made of several hexagonal tiles.

While magnification is an essential feature of a telescope, it isn't the only thing you should consider checking while choosing a device for observations. In general, telescopes may have numerous measures and symbols, but we can distinguish a few which may be handy in determining the possible image properties:

• D_o - The objective's diameter, usually given in mm.
• f_r - f-ratio, it tells us about [the ratio between the focal length and the diameter of the objective (f_r = f_o / D_o). When you find a print like f/8 on your scope, it means that the f-ratio is equal to 8.
• f_e - The eyepiece focal length, as mentioned earlier. As D_o and f_r are usually fixed to the scope (as is the focal length of the telescope), the eyepiece is a changeable element. You can simply make changes to image properties by choosing an eyepiece with another focal length.
• FOV_e - Eyepiece field of view, this is the area described by the angle which is viewable from your point - in this case, using the eyepiece. It typically varies from 50° to 60°. The bigger the value, the greater the fraction of the sky you can analyze at once.

Out of these basic parameters, we can evaluate several different features which tell us about the quality of the image. Fortunately, this telescope magnification calculator will do the job for you! These are:

1. P_r = 115.8" / D_o - Resolving power (or angular resolution), given in arcsec. You can read more about this topic in our angular resolution calculator. We can distinguish two bodies that are separated by an angle greater than P_r. In other cases, they blur into one, becoming a single object. Practically, the smaller the resolving power, the better.

2. FOV_s = FOV_e / M - Scope field of view, analogical to the FOV_e, but this is the overall part of the sky which can be seen as a combination of the objective and the eyepiece. The higher the magnification, the tinier the area you can observe.

3. D_ep = D_o / M - Diameter of the exit pupil, the light beam which exits the scope via the eyepiece forms the so-called exit pupil. The diameter tells about its size.

4. SB = 2 × D_ep² - Surface brightness, given as a percentage of the maximum light intensity per unit area. Remember, it's only the perceived brightness, not the absolute one.

5. L_m = 2 + 5×log(D_o) - Star magnitude limit. You should be able to see objects with an absolute magnitude lower than L_m. Remember that luminosity is a logarithmic function, and lower values mean brighter objects!

6. M_min = D_o / 7 - Minimum magnification, the bottom limit of the magnification, at which the brightness is the greatest. You won't get a brighter image by decreasing the magnification past this point, so there shouldn't be a good reason to do so.

However, some of these values are approximations because they relate to the size of the eye's pupil. We assume that it's around 7 mm in a dark environment, but that likely varies from person to person and generally decreases with age. It's also worth noting that atmospheric disturbances, in particular overcast weather, may lower the quality of the images.

Our tool is straightforward: just look at your scope and input all the necessary values. Let's take a look at an example:

• Find the diameter of the objective - D_o = 135 mm.
• Read the f-ratio - f/5 means f_r = 5.
• Choose an eyepieces, e.g. f_e = 25 mm. If there is no additional information, we can take the default FOV_e value as 52°.
• …and that's all! The telescope magnification calculator evaluates everything else immediately. The resulting magnification is 27, and the resolving power equals 0.86" with the field of view close to 2°. For these conditions, the surface brightness of the image is half of the maximal one.

Try it yourself, and find out what changes if you change your telescope, e.g. using a 10-mm eyepiece!

Want to read more? We highly recommend Randy Culp's presentations, where he explains all of the equations and other interesting features in detail.