Telescope Field of View Calculator

Telescopes open our eyes to the marvel of the cosmos: the telescope field of view calculator will tell you exactly how much!

Here you will learn:

• The basics of telescopes and eyepieces;
• What are the mysterious numbers on an eyepiece?;
• What is the field of view of a telescope?; and
• How to calculate the field of view of a telescope.

And much more. Travel the cosmos from your backyard with Omni Calculator! 💫

Our eyes work pretty okay, but they are absolutely useless when it comes to distant things. It makes sense: we evolved to see predators a hundred meters away, not stars on the other side of the galaxy. That's where telescopes really give us an edge.

A telescope is an optical device that collects light, thanks to a well-thought set of lenses, which focuses and magnifies an image on our retina.

There are two main types of telescopes:

• Refractors; and
• Reflectors.

The difference lies in how they focus the light. Refractors use a lens called an objective lens, while reflectors use a mirror placed at the bottom of the telescope (in this case, the collecting end is called the aperture). Either way, the light gets focused at a certain distance (the focal length), from where it starts diverging again.

It's at this point that the eyepieces enter the scene.

The eyepiece is another lens (or group of lenses) that collects the diverging light rays coming out of the telescope's focal point, and makes them parallel (again: that's how they entered the telescope), thus recreating the image. Two things happened:

• The object got magnified: you can learn more at our telescope magnification calculator; and
• The perceived brightness increased since the light collected from the whole opening of the telescope is now concentrated in a small spot (that's why the bigger the telescopes, the better they are: as they collect more light).

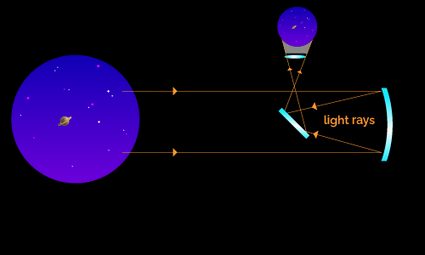
But this is not where it ends. Our knowledge of the universe would be way different if we could explore it only through a pinhole. Luckily, telescope makers learned how to control and tune the telescope's field of view.

The night sky is so distant we can assume it is infinitely so. Even when talking of objects like our neighboring planets and galaxies billions of years away, we perceive them as placed on the same, unreachable plane.

That gives us difficulty specifying distances: can we say, "look three meters on the left of Jupiter"? Clearly, the answer is "no". That's why astronomers measure distances using angles.

What happened? Don't worry. We just moved for a second into deep space! Now, the night sky surrounds you all around. Please take a second to relax, and now, follow us.

We told you that everything in space looks infinitely distant: this is akin to saying, "every object lies on a sphere with radius $r=\infty$". And guess what? You are at the center of that sphere. Do you feel important? You are not, but this is fine.

Now, it's straightforward to think in terms of angles. A sphere is a perfect place to say "two degrees on the left" since every point on it corresponds to a radius converging on the center.

We can use two angles varying from $0\degree$ to $360\degree$ to identify any point on the sphere's surface. And every object has an angular dimension too. The Sun has an approximate angular diameter of $32'$ (the apostrophe indicates the minutes of arc). The Moon's diameter oscillates between $29'$ and $34'$ (this remarkable coincidence makes it possible for humans to witness eclipses). The Andromeda galaxy, M31, has angular dimensions $3\degree 10'$ times $1\degree$, while Neptune is just $2''$ (seconds of arc).

Back to telescopes: the combination of telescope and eyepiece allows you to see a particular portion of the sky, which has an angular diameter called field of view. Is it better to choose, for your telescope, a wide field of view or a narrow one? And what's the definition of telescope field of view? Keep reading!

The field of view, along with the magnification and the opening, is one of the most critical parameters of a telescope.

The larger the field of view, the more you can see at once: at high magnification, this makes the difference between — for example — looking at a single crater or a striking lunar landscape.

Every eyepiece has a specified apparent field of view $\text{fov}_\mathrm{a}$. This quantity defines the angular diameter of the portion of the sky you'd see by looking through the eyepiece alone. The values of $\text{fov}_\mathrm{a}$ varies from $30\degree$ to $110\degree$.

To compute the field of view, we take the value of $\text{fov}_\mathrm{a}$, and we divide it by the magnification $m$ of the combination telescope-eyepiece:

The magnification $m$ is calculated with the ratio of the focal lengths of the telescope $f_\mathrm{t}$ and the eyepiece $f_\mathrm{e}$; thus, we can rewrite the formula as:

As you can see, the field of view of a telescope depends on both the optic tube and the eyepiece. The telescope alone doesn't have a field of view, though there are limits to the portion of the sky it collects light from. The eyepiece is the part defining the width of the field of view. Usually, the field of view doesn't exceed $10\degree$. To give your telescope a wide field of view, mount an eyepiece with an apparent field of view on the "higher-end" of the spectrum and vice versa.

You can find the value of the field of view of your telescope in a few steps with our telescope field of view calculator.

The most basic way to use our calculator is to provide the values of the magnification and the apparent field of view. However, you may not know the magnification: you can either go to our magnification calculator or click on advanced mode.

There are too many types of telescopes and eyepieces out there to create a comprehensive database of their focal lengths. We made two lists with some selected values (the most common in the field); if you can't find the specifications of your set-up, select custom in the drop-down lists.

Tip: Don't know (or can't find) the value of the apparent field of view of the eyepiece you are using? Measure the diameter $d$ of the lens you can see at the bottom of your eyepiece. Multiply it by $57.3$ and use the result to approximate the apparent field of view. You can perform the operation directly in the field of our calculator!

What about an example? Let's take a good set-up, with a magnification of $560\times$ (enough to see the Cassini division in the Saturn's rings), for example, given by a telescope with focal length $f_\mathrm{t} = 2800\ \text{mm}$ and an eyepiece with $f_\mathrm{e}=5\ \text{mm}$. The chosen eyepiece has a $58\degree$ apparent field of view: what is the true field of view?

Saturn has, on average, an angular diameter of $15''$. You can fit around 25 Saturns in your field of view!

Omni tip: at least once in your life, you should see Saturn with your own eyes. We promise it's quite an experience!

We hope our telescope field of view calculator helped you understand the concept of field of view and what those numbers on your instrument mean. Are you looking for something other than telescopes? We covered binoculars, too, in our binoculars range calculator!

If you were looking for the concept of field of view in photography, visit our camera field of view calculator!

The field of view of a telescope measures the size of the portion of the sky associated with a particular set-up. Wide fields of view give you a better view of the surroundings of an object and are ideal for observations of open clusters, nebulae, and the Moon. A smaller field of view helps you focus on the details.

The WFC3 (wide-field camera 3) of the Hubble space telescope has a field of view (in square degrees) equal to 1.98 × 10⁻³ sq. deg., which translates into 25600 square seconds of arc.

The images beamed down to Earth by Hubble when using WFC3 are squares with sides equal to 160", about one-tenth of the diameter of the Moon, from the Earth.

To calculate the field of view of a telescope, you need to find some characteristic values of the setup and an equation:

1. Locate the apparent field of view of the eyepiece.

2. Find the magnification m of the ensemble telescope-eyepiece, or, alternatively:

   • The focal length of the optic tube f_t; and

   • The focal length of the eyepiece fₑ.

3. Then, use the formula:

   fov = fovₐ/m = fovₐ/(f_t/fₑ)

   The result is the diameter of the field of view.

The apparent field of view should be marked on the eyepiece itself. Look for a number followed by the degree symbol, °. Most eyepieces come with an apparent field of view between 30° and 110°. If you really can't find the value, you can approximate it with the formula 57.3 × d, where d is the diameter of the entrance lens of the eyepiece.

The apparent field of view value varies with the magnification on zoom eyepieces.

0.94° or 56.4'. We find this value with the formula for the field of view of a telescope:

fov = fovₐ/m = 75°/80 = 0.94°

This value is almost a full degree, which is enough to contain two times the Moon, or the Nebula Carina, the brightest nebula in the night sky.