Laser Beam Divergence Calculator

Lasers are good but not perfect: learn how — and why — a pointer can't work from the Earth to the Moon with our laser beam divergence calculator!

Keep reading to discover one of the most important features of a laser device. Here you will learn:

• An introduction to lasers and their operations;
• What is the laser beam divergence;
• How to calculate the divergence of a laser beam; and
• How does the divergence of a laser affect the way it propagates.

You will also find some examples and, finally, why pointing at the Moon is rather tricky!

Lasers are devices that emit a highly coherent beam of monochromatic light thanks to a process of amplification of a single wavelength inside an energized medium.

Laser beams have three main properties. We already mentioned two; let's see all of them with an explanation.

• Laser radiation is nearly monochromatic. The characteristic of the medium where the light gets amplified allows selecting almost exclusively a single wavelength of light.
• Laser radiation shows a high directionality. The propagation of a beam happens along an axis around which the light expands rather slowly, even over long distances.
• Laser light is highly coherent. The photons emitted by a laser device are in phase with each other over both time and distance. Coherence allows laser beams to show interference.

The properties of laser radiation made the technology fundamental in the second half of the 20th century. However, when firstly devised, lasers were too "advanced": a scientist said of them that they were "a solution seeking a problem".

Eventually, the problems were found, which allowed the lasers to find applications in many high-technology sectors. The devices are now irreplaceable in medicine, optics, astronomy, manufacturing... you name it!

Meet a laser. It looks like a uniform opaque cylinder from the outside, but you may notice a different material on one of the bases. That's where the radiation escapes the chamber: don't look at it when the device is on!

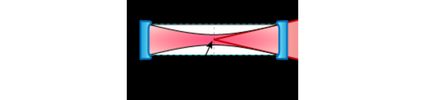
Inside the chamber, you can see two mirrors on opposite and parallel sides. One of them (the one at the opening of the resonator) is partially transparent, while the other is fully reflective.

Between the two mirrors, you can find a medium. This material constitutes the core of the device. If pumped with energy (either electricity or light), it can amplify the light of a specific wavelength. After bouncing back and forth many times, the photons escape the chamber, amplified and coherent.

The beam acquires its properties inside the optical resonator. We are talking about the three features listed above plus the way it propagates. Ideal lasers are Gaussian beams, which means that they move along a primary direction — or axis — with a cross-sectional intensity profile following a Gaussian curve.

The beam reaches its smallest size at a particular point in the resonating chamber. We call that point the waist of the beam. Once the beam passes the waist, it starts expanding in a cone. The angle of expansion is the divergence of the beam. Let's analyze it in detail.

The divergence of a laser beam measures how much the beam spreads with the distance, that is, the rate at which the laser diameter increases.

The diameter of the beam is measured at the $1/e^2$ intensity point: the distance from the peak at which the intensity drops to $1/e^2$ of the maximum value. The cone described by the divergence angle contains $86\%$ of the total power of the laser.

All of the calculations for the divergence of a laser beam rely on the far-field approximation. Take a look at the diagram below. Close to the waist, the beam expands following a smooth curve. If you measured the divergence around that area, you would get the wrong result, underestimating the actual value. If you move far from the waist, the beam diameter increases almost linearly with the propagation direction. This situation is what we call far-field approximation.

The formula for the divergence angle of a laser beam is:

In the formula, we can identify:

• $D_{\text{f}}$ — The diameter of the beam measured in the final point;
• $D_{\text{i}}$ — The diameter of the beam measured at the initial point; and
• $l$ — The distance between the initial and final point.

Notice how we measure twice the angle between the $1/e^2$ asymptote and the propagation direction.

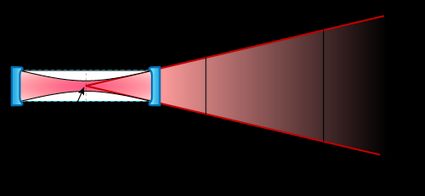
The previous formula for the divergence of a laser beam arises from geometrical considerations. As you can see in the diagram above, we ignore the structure of the Gaussian beam and only consider rays propagating in straight lines.

The divergence of a laser beam is limited by the physical characteristic of the laser itself. For ideal beams (propagating in a Gaussian beam with quality factor $M^2=1$), the divergence can't be lower than twice the value given by the formula:

where:

• $\lambda$ — Wavelength of the laser (or the frequency, if you apply the correct formula as in our wavelength calculator);
• $w_0$ — Diameter at the waist; and
• $M^2$ — Beam quality parameter.

Our laser beam divergence calculator calculates the divergence of the beam in the far-field limit. You only have to input the values of the diameters at the initial and final points and the distance between the two. We will calculate the rest.

In advanced mode, you can find the fields for the optional variables wavelength, waist diameter, and quality factor of the beam. If you insert them, we will fire a warning if your calculations will return a value below the minimal theoretical limit of divergence. If you leave them empty, the only alert that will fire is if the divergence calculation returns a negative value.

Let's now calculate the divergence angle of a laser beam. Consider a beam with initial diameter $D_{\text{i}}= 4\ \text{mm}$. Let's move away from the source by a distance $l=10\ \text{m}$, and measure the diameter again. We find $D_{\text{f}}=7.5\ \text{mm}$. This information is all we need to calculate the divergence of that beam. Input the values in the LASER beam divergence calculator.

We will apply the formula for the divergence of a laser:

This value is small but not that small for lasers. You can use our calculator in reverse too: insert the distance, the initial diameter, and the divergence, and find out the final diameter of the beam. In this case, at the distance of $1\ \text{km}$ the beam would be more than $35\ \text{cm}$ in diameter.

We made other laser-related calculators! Discover more about those fascinating devices with our:

• Laser brightness calculator;
• Laser linewidth and bandwidth calculator; and
• Laser beam spot size calculator.

The lasers we see normally operate at relatively small distances, and we may be bound to think that they can propagate for an arbitrarily long distance without losing their characteristic "dot" shape.

Say this to an astronomer, and he will surely disagree. When the distances increase, lasers reach their limits while still maintaining an edge over traditional light sources.

Consider the process of lunar ranging, the measurement of the distance between Earth and Moon through the reflection of laser pulses on the reflectors left by space missions on the surface of our satellite.

In a typical lunar ranging experiment, a telescope collimates a laser (thus achieving a small divergence) and shoots the beam in the direction of the Moon, trying to hit the area of the reflector. This task is not like shooting at the broad side of a barn: the reflectors are incredibly tiny, and even though their locations are known, the sheer distance between them and us makes every hit a success.

The beam expands on its way to the Moon, reaching the surface of our satellite with a diameter of roughly $2\ \text{km}$. The telescope sending the pulse has a diameter of $3.5\ \text{m}$. Considering the mean value of the distance between Earth and Moon $(384,400\ \text{km})$, we can calculate the divergence of the beam:

Which corresponds to barely more than a second of arc. This is an impressive feat! The pulse would be technically invisible by a human eye on the Moon, and its photons must still travel all the way back to Earth, undergoing further divergence. Catching a reflected photon is as hard as looking for a needle in a haystack. Luckily, scientists send a lot of photons at the same time, making detection possible.

The divergence of a laser beam is the measure of the increase in the beam diameter over distance. Even though lasers have a high directionality, the light propagates following a Gaussian beam, expanding over time.

The laser beam divergence is measured by an angle, often the full angle of the beam.

To calculate the divergence of a laser beam in the far field approximation, be sure to know:

• The initial diameter of the beam Di;
• The final diameter of the beam Df;
• The distance between the two measurement points l.

Then:

1. Compute the difference between final and initial diameter: Df - Di.
2. Compute the ratio between the difference and twice the distance l: (Df - Di)/(2 × l).
3. Compute the arc tangent of the ratio and multiply by 2.

Express your result in milliradians: the divergence is often pretty small.

You can reduce the divergence of a laser by acting on a single parameter, the initial diameter of the beam. Increasing it helps increase both the Rayleigh range (thus increasing the coherence length) and the divergence.

You can easily see this effect by observing the laser beam divergence formula and varying the value of the initial diameter Di:

ϴ = 2 × arctan((Df - Di)/(2 × l))

You can collimate the beam using a lens or a telescope to achieve such an effect.

0.4 mrad. To find this value, simply plug the values:

• Initial diameter Di = 1 mm;
• Final diameter Df = 5 mm; and
• Distance l = 10 m

...into the formula for the laser beam divergence:

ϴ = 2 × arctan((5 - 1)/(2 × 10,000)) = 0.4 mrad