Laser Beam Spot Size Calculator

Learn how to calculate the spot size of a laser beam with our dedicated tool. Initially, it can look complex, but we will guide you through a detailed explanation of the physics of the problem, teach you how to calculate the laser beam spot size after introducing all the necessary quantities, and end the article with some practical examples.

Here you will learn:

• What are lasers in a nutshell.
• When do we talk about laser beam spot size at focus?
• The laser beam spot size equation.
• What is the laser depth of focus?
• The laser depth of focus equation.

Be laser-focused and follow us in exploring this tiny spot of optics!

Lasers are sources of coherent light, which means that the light waves are in phase over a certain distance (the coherence length), thus maintaining their focus and small beam size.

The name LASER is the acronym for "light amplification by stimulated emission of radiation", which describes the principal characteristic of the device itself: by pumping a medium where a specific light frequency may appear, we obtain the amplification of such frequency and subsequent emission.

Lasers are widely used in many fields, from entertainment to medicine, from the military to advanced scientific research. Saying that they lighted the way to see the world with different eyes is not an understatement.

In the diagram below, you can see the path of a laser beam from the emission to its focusing on a small spot. On the left, we find the emitter, followed by the collimating lens that corrects the divergence. Let's check these first steps.

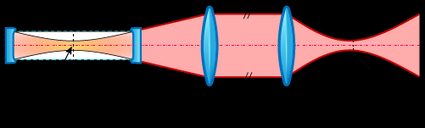
Laser emitters select a specific wavelength of light inside an amplification medium contained in a resonating optical cavity. The light gets amplified by repeatedly bouncing back and forth between two mirrors on the two sides of the cavity, traveling through the energized medium. One of the mirrors on the resonator side is partially transparent and allows the amplified wavelength to escape the camber.

Laser beams propagate following — ideally — the equation of a Gaussian beam, where the amplitude envelope follows the Gaussian function, with a smooth peak in the center, surrounded by decreasing tails.

Right after their emission, laser beams diverge. We talked about this in detail in our laser divergence calculator. Even though the beam is more collimated than one of the other light sources (light bulbs, to name one), thanks to the coherency of the beam, this doesn't prevent the beam spot from spreading after a certain distance.

When necessary, it's typical to collimate the laser beam through a lens that collects the weakly divergent rays coming from the optical resonator and straightens them, allowing for a longer coherence distance.

One of the uses of collimated laser beams is optic fiber communication. A well-collimated laser can propagate for long distances in the "comfortable" medium of fibers, only needing some amplification on the way.

When the laser beam reaches its destination, you may want to focus it, concentrating its power in a small spot. Think of laser cutters, mainly, but also the standard pointers. A lens is often included to keep the divergence at bay. How small can we focus our beam?

We are now in the last part of our diagram. The collimated beans reach a lens with focal length(learn what is this quantity with out focal length calculator) $f$ that focuses the beam in a single, small spot with diameter $S$. We created a new Gaussian beam with all the characteristics of the previous one, just different values. In particular, we have a new waist.

To calculate the new waist, we need to introduce the laser beam spot size equation:

$S$ is the spot size at the focal length (its diameter). The other parameters we need to introduce are:

• $\lambda$ – Wavelength of the laser;
• $d$ – Diameter of the beam at the lens surface;
• $f$ – Focal length of the lens; and
• $M^2$ – Beam quality parameter

The beam quality parameter $M^2$ is a measure of how much a laser beam deviates from the ideal Gaussian beam (which corresponds to $M^2=1$).

This equation is straightforward with its implications. The size of the beam spot is directly proportional to the lens's focal length. A shorter focal length makes for a highly focused beam. However, there's a tradeoff: the more focused the beam is, the higher its divergence, and in a short distance past the focal length, the beam would lose its laser properties.

After reaching the focus, the laser beam gets wider, losing its small beam spot size and progressively resembling a "normal" source of light.

Physicists decided to quantify this loss of focus through an appositely set quantity called the Rayleigh range: the distance from the waist (or any focusing point) at which the beam spot size doubles its area (which corresponds to an increase of $\sqrt{2}$ of the diameter). A laser beam's depth of focus corresponds to twice the Rayleigh range: when we move past this distance, the laser loses its sharpness and coherence.

The Rayleigh range equation is:

The equation for the laser depth of focus is:

where:

• $z_{\text{R}}$ – Rayleigh range; and
• $S$ – Minimal diameter of the beam.

Our laser beam spot size calculator will give you the answer to your problems at the speed of light. You only have to provide us with the numbers of the parameters you know, and we will calculate the result for both the laser beam spot size and the depth of focus.

Let's consider an example. We will study a green laser with wavelength $532\ \text{nm}$, slightly deviating from a Gaussian beam: the quality parameter is $M=1.12$. Assume it reaches a lens with focal length $5\ \text{cm}$ with a diameter of $0.5\ \text{mm}$.

We have all the ingredients to calculate the laser beam spot size at the focal length:

You can see that this is not all! Our tool calculated the depth of focus too:

You can increase the depth of focus (hence maintaining a high quality of the beam for a longer distance) by lengthening the lens's focal length. However, as you can see in our calculator, this is detrimental to the size of the spot (which increases).

To calculate the spot size of a laser beam, you need to know the setup of your optical system. Be sure to know the following:

1. Wavelength of your laser λ;
2. Diameter of the beam at the lens d;
3. Focal length of the lens f; and
4. Beam quality factor M².

Once you know the parameters, feed them into the laser beam spot size equation:

S = (4 × M² × λ × f)/(π × d)

The spot size of a laser beam cutter ranges from 15 μm to 170 μm (0.003 to 0.007 inches), depending on the lens you are mounting.

The shorter the focal length of the lens, the smaller the spot, which allows for the engraving of finer details. However, smaller spots are not suitable for working with thick materials.

The Rayleigh range is the distance from the waist at which a laser beam's area becomes twice its minimum value. At a distance of two times the Rayleigh range, the sharpness of the beam is insufficient to operate the laser (for imaging, cutting, etc.). The Rayleigh range is closely related to the divergence of a beam.

8.28 μm. We assumed that:

• The wavelength is λ = 650 nm; and
• The beam is ideal: M² = 1.

Plug the values in the equation for the laser beam spot size, and find the result:

S = (4 × M² × λ × f)/(π × d) = (4 × (650 × 10⁻⁶) × 100)/(π × 10) = 0.00828 mm = 8.28 μm

The effect of the laser beam quality on the spot size is directly related to a deviation from the ideality of the beam. The ideal value of M² is 1, which corresponds to an ideal Gaussian beam.

An ideal Gaussian beam has the smallest possible spot size, thus preventing M² from assuming values smaller than 1. The spot size S increases with M² for any other value.