Inclined Plane Calculator

This inclined plane calculator is a tool that helps you solve problems about an inclined plane with the friction coefficient taken into consideration. Read on to find the inclined plane definition and common computational inclined plane examples.

An inclined plane can be described as a flat surface that is lifted at one side to form an angle θ with the ground. You can find the examples of inclined planes in everyday life, such as ramps or door wedges. A funicular is a type of transport vehicle that also uses the concept of the inclined plane. The idea behind the simplicity and usefulness of the inclined plane is to reduce the force required to lift a body to some height.

An inclined plane is one of the most common simple machines, together with the lever. Discover the latter at our lever calculator!

There are a few characteristics that can adequately describe a simple inclined plane. The primary one is the slope associated with the already mentioned angle θ. The next ones are height (H) which is the maximal level above the ground, and length (L) – the distance between the apex and the vertex at the angle θ. The side view of an inclined plane can be presented as a right triangle, so you can easily find a relationship between H, L, and θ if needed.

Friction coefficient is another feature of the inclined plane, and it denotes the existence of a braking force that affects the body in motion or prevents the object from moving at all.

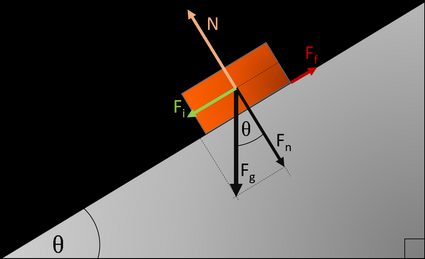
While working out problems of this type, it is always worth finding forces which act on our body:

1. Gravitational force: $F_g = m \times g$, where $m$ is the mass of object and $g$ is the gravitational constant. It can be divided into two components:

   • $F_i = F_g \times \sin\theta$ – parallel to inclined plane; and
   • $F_n = F_g \times\cos\theta$ – perpendicular one.

2. Force of friction which works in the opposite direction as $F_i$, but depends on the value of normal force $F_n$ and friction coefficient $f$:

   $F_f = f \times F_n$

3. There is also ground reaction force $N$ with the same value as $F_n$ and the opposite direction, but it doesn't have any influence on further calculations

The resultant force $F$ along the inclined plane can be worked out as a difference between $F_i$ and $F_f$ and thus rewritten as:

One important note: the above expression of the net force is only valid if the angle of the inclined plane is not greater than the angle of friction $\theta_f$, which can be estimated as $\tan\theta_f = f$. Otherwise, the friction force compensates $F_i$, and the object stays at rest.

With the known expression of the resultant force, it is a piece of cake to find acceleration $a$, sliding time $t$, and final velocity $V$, using formulas from the acceleration calculator and the value of initial velocity $V_0$:

If the object starts moving without initial velocity, the expression for sliding time simplifies to:

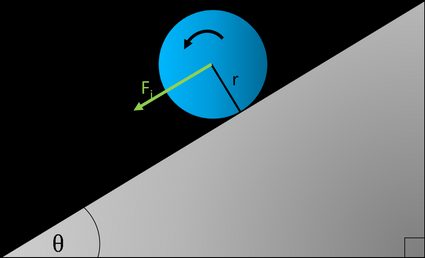
It isn't difficult to imagine some round object which would rather roll down instead of sliding. Therefore, a different approach has to be adopted for rotary bodies. This time friction prevents objects from slippage and simultaneously allows rotation. We can repeat the calculating process from the previous section, taking into account both progressive and circular motions, which is quite tricky. Still, on the other hand, we can use the conservation of energy.

It tells us that the sum of initial potential and kinetic energies equals the final kinetic energy. It's essential to remember that rotational kinetic energy is fixed in total kinetic energy. The acceleration formula changes as follows:

where $I$ is the object's moment of inertia and $r$ is the radius between the axis of rotation and the surface of the inclined plane, which is usually equivalent to the body's radius (e.g., ball or cylinder). The remaining expressions for rolling time $t$ and final velocity $V$ are precisely the same as previously.

If you're wondering how we arrived at this equation, make sure to read up on the potential energy formula.

Example 1

Let's assume that we need to find the sliding time and the final velocity of a sliding object with these input data: $m = 2\ \text{kg}$, $\theta = 40\degree$, $f = 0.2$, $H = 5\ \text m$, $V_0 = 0$. You can obtain the solution with the following steps:

1. Calculate the gravitational force:

2. Divide it into two perpendicular components:

3. Determine the friction force:

4. Subtract $F_i$F and $F_f$ to work out the resultant force:

5. Thus, acceleration can be derived:

6. The length of the inclined plane equals:

7. So the sliding time can be obtained:

and also the final velocity:

We can also estimate the energy loss, which is the difference between the initial potential energy and the final kinetic one:

The total energy isn't conserved, which is caused by the work done by the friction force. It's usually released in the form of heat.

Example 2

In the second example, let's find the same parameter, but with different values of input data: $m = 2\ \rm{kg}$, $θ = 20\degree$, $f = 0.5$, $H = 5\ \rm m$, $V_0 = 0$.

Firstly, we can work out the angle of friction for a given friction coefficient:

...which is greater than our angle $\theta$.

It means that the body won't move due to sufficiently high friction force! As a result, we don't even have to repeat all these steps from the previous example because the object can't slide down without any external force.

Example 3

The last example uses the following data: $m = 2\ \rm{kg}$, $θ = 90\degree$, $f = 0$, $H = 5\ \rm m$, $V_0 = 0$. At first glance it may look strange, but let's try to solve it:

It turns out that the acceleration equals the gravitational one. The angle $\theta = 90\degree$ denotes vertical movement, and $f = 0$ indicates the lack of resistance, which means we are facing the problem of free fall. Once you notice this, you can find the sliding (falling) time with free fall calculator: $t = 1.010\ s$.

However, all these results can be estimated without great effort, regardless of any further assumptions – just use our inclined plane calculator!

To conclude, let's find out the rolling time of a ball for initial inclined plane parameters $\theta = 30\degree$, $H = 5\ \rm m$ and $V_0 = 0$. The moment of inertia of a solid ball equals $I = 2/5 \times m \times r^2$. We can start with extending the formula for acceleration, remembering that the resulting force is $F_i = mg\sin\theta$:

We can see that the expression for $a$ simplifies significantly, and actually, there is a general rule which says that for bodies with the moment of inertia in the form of $I = kmr^2$ (where $k$ is some constant factor) we can figure out the acceleration as:

It's really striking that the result depends neither on mass nor the size of the ball! The rest is a well-known procedure: