Angle of Banking Calculator

A turning road is not flat, it's tilted: with our angle of banking calculator, you will discover why!

Some simple physical considerations and some math will be enough to understand something that seems trivial but has consequences for our safety when driving: tilted turns. With a world going faster and faster by the day, a slightly oblique road can make the difference between staying on the road and not. Here you will learn:

• How a vehicle behaves in a turn;
• How to solve the problem of turns at high speed;
• The mathematical derivation of the angle of banking equation;
• What is the angle of banking in aircraft;
• How to use our angle of banking calculator.

When turning a vehicle, like a car, we move it from a straight trajectory. Physics tells us that we need to apply a force in the desired direction: in the case of a turn, this is the centripetal force, which points to the turn's center.

Consider now a turn on a flat surface and the absence of forces besides gravity and friction. The only force that can counteract the centripetal one is friction. The frictional force $F_f$ is a function of the mass $m$ of the object and the friction coefficient $\mu$:

To keep the car on track, the force due to friction must be bigger (or equal, at least) to the centripetal force:

Above, $v$ is the vehicle's speed and $r$ is the radius of the turn.

How can we facilitate things? Enter the tilted turn.

Suppose you tilt the road at a certain angle $\theta$, the angle of banking. In that case, the forces acting on the car will break into components, and by carefully tuning the angle, engineers can design the safest road for a given speed.

We can consider two situations: with and without friction. In the first one, the only forces acting on the vehicle are gravity and centripetal force: there is no friction to help to steer.

We will study the tilted turn using the formalism of the inclined plane — the same we met at the inclined plane calculator — but from a different perspective. Consider the normal force $F_N$, perpendicular to the plane, and consider its vertical and horizontal components. What's the normal force? Glad you asked: our normal force calculator is here to help!

Notice that usually, we consider the normal force a component itself.

The two components (obtained with the sine and cosine, we met those at the trigonometric functions calculator) are:

• The vertical component, which is nothing but the weight of the vehicle;
• The horizontal component, which equals the centripetal force.

Let's consider the horizontal one first:

And the vertical:

Rearranging them to isolate $F_{N}$ results in the equality:

Now we can find the velocity at which we can engage a turn with a specified range and angle of banking.

Notice how the mass cancels out — this often happens in physics. The daily experience suggests that the mass is important, but this is often the result of real-life, more complex phenomena. If you ignore outside forces and assume spherical cows, the mass disappears from the equation, like in a free fall.

Let's introduce friction in our tilted turn! We will write the formulas first and then take a closer look at them.

We can now see a friction force parallel to the turn. We can decompose that one too in horizontal and vertical components, which will eventually contribute to the total force acting on the vehicle. When friction appears, we can identify a range of speeds at which the vehicle can approach the turn. When driving at the maximum speed, the friction points inward: going above that speed would make the vehicle skid out of the turn. The minimal speed sees the vehicle "falling" toward the center of the turn: the friction points outward.

Let's analyze the maximum speed case first.

The horizontal component, the one contributing to the centripetal force, is:

The centripetal force now receives two contributions: as a result, the angle can be smaller while keeping the speed unvaried.

To isolate the speed, we need to consider the vertical component too: in this case, the friction force adds a downward contribution:

To calculate the minimum speed equations, simply invert the signs of the friction terms. Now rearrange the equations to isolate the speed as we've seen in the frictionless case:

Where choosing $+$ at the numerator gives the maximum speed, whereas $-$ returns the minimum one. Remember to choose the correct sign at the denominator, too!

What if it's not the road to tilt, but the vehicle? That's what happens with planes. The set of equations to calculate the angle of banking for an aircraft is slightly different.

First thing: we need to think in terms of lift, the vertical force that counteracts the weight of a plane. The lift point upwards and equals the aircraft's weight in level flight. In a turn, the lift changes direction, pointing towards the center of the turn, thus creating the component of centripetal force we need.

The sequence of actions needed to steer an aircraft is:

• Roll the aircraft of an angle $\theta$, lowering the wing in the direction of the center of the turn;
• Pull the yoke.

Congrats, you now know how to steer a plane!

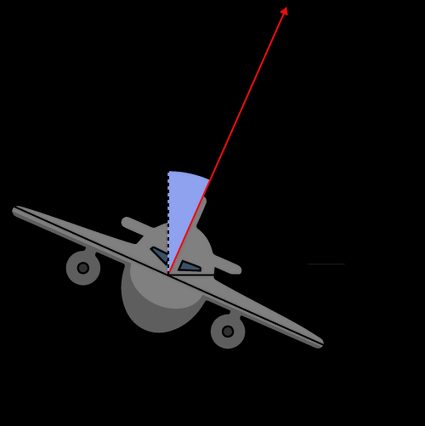
Pulling on the cloche increases the lift, which now outmatches the weight. The excess horizontal component contributes to the centripetal force.

The two components of the lift are:

Since an aircraft can't really get thrown off the road — there are no roads in the sky — the airspeed is usually specified in the calculation instead of the radius, leaving the latter as the unknown of the equation. The angle of banking equation is:

To find the angle of banking, you need to reverse the equations used to find either the speed or turning radius.

For a vehicle on a fixed-design road, the equation for the angle of banking is:

where $\arctan$ is the inverse tangent function. For an aircraft, the angle of banking equation is:

A usual value for the tilt of a curve on highways is 7% — if snow is unlikely. This angle corresponds to $\theta=4\degree$. The radius of the turn is $500\ \text{m}$. It didn't rain, so we get a nice friction coefficient $\mu = 0.7$.

Let's first assume a flat road: what is the maximum speed we can go before falling off the tracks? Set $\theta = 0\degree$.

Rather high, isn't it? Engineers are known to play safe!

What about the minimum speed? It is undefined since you can't fall from a flat road! Let's check what happens when we tilt the road.

Well, that's a noticeable increase! Let's check the minimum speed now: again undefined. That's because of the relatively low bank angle. Take a look at the circuits of NASCAR races: the tilt is noticeable there, and the risk of sliding down is not negligible!

What about planes? Let's say you are flying in an SR71, at the ludicrous speed of $3,951\ \text{km}/\text{s}$ — more than three times the speed of sound! If you want to turn remaining inside the territory of Ohio, you have to keep your turning radius at $150\ \text{km}$. Let's find the banking angle!

This is a lot! But we guess it's not that hard to go fast with those engines!

Everything you read in the article is in our angle of banking calculator!

First, choose if you are a car or an airplane. Erm... that's if you are even studying a problem involving a car or an airplane. This will give you the right set of equations to work on.

Next choice, the direction: choose if you want to find the speed (or radius) or the angle of banking.

Now you are all set! Insert the values you know in our calculator, and we will do the math for you. 😀

We hope our angle of banking calculator helped you, both in your physics problems and in satisfying your curiosity!