Linear Actuator Force Calculator

If you are looking for an easier way to calculate the force required for your linear actuator, our linear actuator force calculator is a perfect solution for you. Our tool gives you the ability to get a first-hand estimation of the maximum force required for an actuator via two demo configurations: inclined platform and horizontal-flat platform.

Moreover, our calculator is a general-purpose tool that can compute the maximum force required for different types of actuators: hydraulic actuators, pneumatic actuators, and electromechanical actuators.

Now that you know about some essential points of our calculator, please read the article below to learn about:

• How the linear actuator force calculator works; and
• What equations and approximations are used behind the scenes?

A linear actuator is an actuator that provides motion along a line or in one direction by using mechanical energy converted from other forms of energy. Linear actuators are versatile mechanisms used in almost all industries: from food processing to the aerospace industry.

Linear actuators are mainly categorized into three types based on the source used to produce mechanical energy. They are:

• Hydraulic actuators – Uses energy stored in a liquid to generate mechanical motion.
• Pneumatic actuators – Employs energy stored in a gas to yield mechanical motion.
• Electro-mechanical actuators – Utilizes electrical energy to generate mechanical motion.

Our calculator includes two different application cases. Each is built using Newton's law of motion: if you need to refresh it, visit Omni's Newton's second law calculator. Two application cases are:

• First case: An inclined plane with an actuator moving against gravity.
• Second case: Horizontal plane with an actuator moving the block of mass along the horizontal surface.

Let us understand how Newton's law is applied for the first case. The figure below shows the schematic and the corresponding free body diagram (FBD) for an inclined plane case with the actuator pushing the block against gravity.

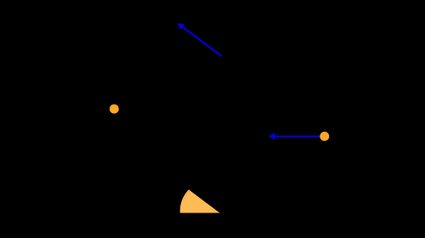
The forces involved are:

• Weight $mg$ is acting in the perpendicular direction to the ground surface (where $m$ is the mass, and $g$ is gravitational acceleration).

  This force is decomposed into two components: $mg\sin(\theta)$ and $mg\cos(\theta)$.

  • $mg\cos(\theta)$ is the force acting perpendicular and into the inclined surface.
  • $mg\sin(\theta)$ acting in the direction parallel to the inclined surface and opposite to the actuator force $T$ direction.

• The normal force $N$ is equal in magnitude to $mg\cos(\theta)$ but acts in the opposite direction ,i.e., perpendicular and outward to the inclined surface.

• Next, you have a friction force. Since we are dealing with a maximum force calculation, we need to consider static friction. The static friction force $F_{\mathrm{f}}$ (indicated by the $>>>$ symbol in the free body diagram) is equal to the product of the coefficient of static friction $\mu$ and normal force $N$, i.e., $F_{\mathrm{f}}=\mu N$

The decomposition of the forces on an inclined plane is thoroughly explained at the inclined plane calculator: check it out!

• Finally, we have the force due to inertia. It is given by (indicated by the $>>$ symbol in the free body diagram): $F_a=ma$, where $m$ is the mass of the object and $a$ is the acceleration that depends on velocity change and the time required for the velocity change.

  We are dealing with maximum force calculation, as a result, we assume that velocity changes from $0\ \mathrm{m/s}$ at time $0\mathrm{\ s}$ to velocity $V_{\mathrm{M}}\ \text{m/s}$ at time $t_{\mathrm{stroke}}$. Here, $t_{\mathrm{stroke}}$ is the time required for the actuator to complete the stroke length $l_{\mathrm{stroke}}$. Therefore, the velocity $V_{\mathrm{M}}$ is given by:

Hence, the acceleration and in turn the inertial force respectively are:
* Acceleration: $a=l_{\mathrm{stroke}}/t_{\mathrm{stroke}}^2$
* Inertial force: $F_{\mathrm{a}}=ma$

Now, our actuator force $T$ should counter all the above forces to succeed in moving the block. The force balance is given as:

Using the above equation, you can obtain the maximum force required by the actuator to move the block on an inclined plane against gravity.

Next, let us look at the horizontal case. In the figure below, you will notice the horizontal plane case.

By following similar reasoning as in the first case, the force balance equation coming from newton’s law is written as:

The notations used here are similar to the first case (inclined surface case).

The main difference between the first and second cases is the absence of a direct effect of gravity (the term $mg$) in the second case. But the gravity effect manifests itself indirectly through friction force ($\mu mg$) in the second case.

Important limitations of our linear actuator force calculator are indicated below:

• Our calculator assumes that the piston velocity changes from 0 to $V_{M}$ without including any velocity profile. As a result, you can only use our calculator as a first-hand approximation.

• Our calculator assumes only an application where we try to move a block. As a result, it cannot be used for rotational motion applications.

In this section, you will get step-by-step instructions to use our calculator efficiently:

1. First, choose the type of set-up that suits your application via the Actuator type option.
2. Now, insert the parameters that decide the requirements of the actuator:
   • Insert the mass of the object that needs to be moved in the Load mass field.
   • Insert the stroke time and stroke length required.
   • Finally, insert the static friction coefficient between the object that needs to be moved and the surface.
   • If you have chosen inclined surface as the actuator type, you must insert the inclination angle.
3. After inserting all the parameters, our calculator will output the following result:
   • Actuator velocity;
   • Actuator acceleration; and
   • Actuator force.

Excellent, now you know how to use our calculator efficiently! If you are curious about how a piston and cylinder arrangement produces the required force, check out our piston force calculator and hydraulic pressure calculator.

Let us look at our calculator in action. Consider an inclined surface case, and the following are the problem parameters:

• Block of mass of $\text{150 kg}$ on an inclined surface.
• Block should be moved by $\text{10 m}$ in $\text{40 seconds}$.
• Static coefficient of friction between the surface and the block is $0.68$.
• Inclination angle of the inclined surface is $\text{25 degrees}$.

10 m is your stroke length and 40 seconds is your stroke time. By keeping this mind, now insert the above parameters into our calculator to obtain:

• Actuator velocity = $0.25\ \text{m}/ \text{s}$
• Actuator acceleration = $0.00625\ \text{m}/\text{s}^2$
• Actuator force = $1529.69\ \text{N}$

Once you find the maximum force, go to the vendors' website and check for a suitable linear actuator!

Stroke length is the maximum linear motion that can be obtained by a linear actuator. The stroke length needs to be long enough to perform the required action but small enough to fit in the available space. When fully retracted, a linear actuator will be the length of the stoke, plus the motor, gearbox, housing, etc.

You can decompose the force vector by using the following steps:

1. Find the inclination angle: the inclination of the force vector with respect to the x-axis.
2. Multiple the inclined force vector magnitude and sin of the incline angle to find the y-axis component of the force vector.
3. Multiple the inclined force vector magnitude and cos of the incline angle to find the x-axis component of the force vector.

You need a force greater than 98.1 N to lift a 10 kg object. To obtain 98.1 N: you multiply the mass of an object (10 kg) by the acceleration due to gravity (9.81 m/s²).