Hydraulic Pressure Calculator
This hydraulic pressure calculator analyzes a hydraulic system of two pistons connected to each other via a medium, usually a liquid. Such devices are usually used in situations where you have to lift something heavy using a lower force, e.g., automobile hydraulic lift in service stations. You can find mechanical analogy of hydraulic press in our mechanical advantage calculator, where we have described six simple machines such as a lever, a pulley or a wedge.
The basic principle of the hydraulic press is based on the so-called Pascal's law (also Pascal's principle). Read on if you want to learn what is Pascal's principle and how to use it to estimate appropriate areas of the pistons and the forces exerted on them. In the following text, we have also provided an example of hydraulics calculations which can be done with our Pascal's law calculator.
What is Pascal's principle?
The Pascal's law says that if you apply external pressure on the liquid of gas in the enclosed container, the pressure will be transmitted throughout the fluid so that the same shift occurs everywhere. This law was named after Blaise Pascal who in 1646 performed an experiment called Pascal's barrel. He inserted a long vertical tube into a barrel filled with water. Then he poured the water into this tube, which increased the hydrostatic pressure. At some point, the pressure inside the barrel was too high and the barrel burst.
Pascal's principle is used in many hydraulic systems, such as hydraulic press, which is shown in the figure below. There are two pistons: one with a smaller area and one with a bigger area that are connected with each other via some hydraulic fluid. The pressure that the smaller piston exerts against the liquid will be precisely equal to the pressure the liquid exerts against the bigger cylinder. It is important to stress that not the forces, but pressures are equal.
Figure from: https://en.wikipedia.org/wiki/Hydraulic_drive_system
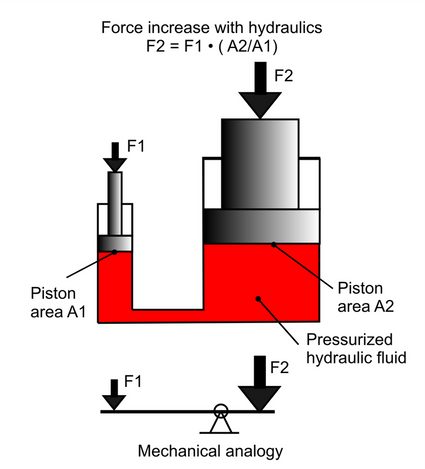
Pascal's law calculator
Our hydraulic pressure calculator can compute suitable parameters of both pistons in the hydraulic press. To do this, we have used Pascal's law formula, which after appropriate transformations takes the form of:
F₁ = A₁ / A₂ * F₂
where
F₁is the force applied to the first piston,F₂is the force applied to the second piston,A₁is the area of the first piston,A₂is the area of the second piston.
The pressure of the liquid inside the hydraulic press can be calculated in two simple ways: p = F₁/A₁ or p = F₂/A₂. Although this is not obvious at first, the principle of energy conservation is fulfilled in the hydraulic press. To lift a heavier object lying on the first piston, we need to move the second piston at the longer distance. We can express it with these equations:
d₁ = F₂ / F₁ * d₂ or d₁ = A₂ / A₁ * d₂
d₁is the distance at which the first piston has moved,d₂is the distance at which the second piston has moved.
The total work done by one piston satisfies the relation:
W = F₁ * d₁ = F₂ * d₂
In the advanced mode of our hydraulic pressure calculator, you can also estimate parameters: d₁, d₂ and W.
Hydraulic calculations
Let's use our hydraulic press calculator to analyze automobile hydraulic lift. How much force do we need to apply to lift a car with the mass 1000 kg? Let's go step by step:
- Pressure is usually exerted on fluid in the small piston by a compressor. If you assume that the small piston is a circle with a diameter of
3 cmthen you easily compute that its area equalsA₁ = 7.069 cm²(you can use our circle calculator to compute the area of the circle). - Similarly, if the bigger piston, which lifts the car, is a circle with
30 cmin diameter then its area equalsA₂ = 706.9 cm². - The weight of car with mass of
1000 kgisF₂ = 1000 kg * 9.80665 m / s² = 98066.5 N, because Earth's acceleration isg = 9.80665 m / s². - Finally, with our Pascal's law calculator we can calculate that to lift a car with a mass of
1000 kgwe need onlyF₁ = 980.7 Nwhich corresponds to the mass100 kg, approximately a mass of human body! At the same time, the liquid pressure isp = 1387.3 kPawhich is13.69times higher than the atmospheric pressure. Check out pressure conversion calculator to learn how you can switch between different pressure units. - In the advanced mode of the hydraulic pressure calculator, you can also estimate how far a smaller piston should be pushed to lift the car, for example, at
10 cm. After simple calculations, the answer is10 m, which is relatively long.
