Last updated: Jul 28, 2024

Distance to Horizon Calculator

Q: How far would I see on the Moon?

The horizon for an average human 1.75 m tall would be about 2.5 km . As the Moon is smaller than Earth , the horizon on our satellite would be closer than Earth's. To compute the distance of the horizon on the Moon, follow these easy steps: Sum the radius of the Moon and your height, and compute the square of the result: (1,737,500 + 1.75)² . Subtract the result to the square of the Moon's radius: 1,737,500² . Take the square root of the result: √((1,737,500 + 1.75)² - 1,737,500²) = 2,466 m ≈ 2.5 km .

Q: How do you calculate the distance to the horizon?

To compute the distance to the horizon , we follow these easy steps: Compute the sum of the radius of Earth and the height of the observer . Calculate the square of Earth's radius . Subtract the result of step 2. from the result of step 1., and take the square root . The result is the distance to the horizon. We calculated it using Pythagoras' theorem on a right triangle with corners in the center of Earth, the observer, and the horizon.

Q: What is the distance to the horizon if I'm 1.75 m tall?

On Earth, with an unobstructed view , the distance to the horizon calculated for a height of 1.75 m would be approximately 4.7 km . To find this result, use the formula for the distance to the horizon: d = √((r + h)² - r²) where: d — Distance to the horizon; r — Earth's radius ( r = 6,371,008 m ); and h — Height of the observer ( h = 1.75 m ). Substitute these values in the formula to find the result.

Q: How high should I be to see 10 km away?

Not as high as you would imagine: 7.85 meters above the ground would be enough to see as far as ten kilometers away . We used the inverse formula for the distance to the horizon. Start with the distance to the horizon equation: d = √((r + h)² - r²) . Rewrite it for h . You'll find a quadratic equation: h² + 2rh - d² = 0 Take the positive root of the equation: h = 1/2 · (-2r + √(4r² - 4d²)) Substitute d = 10,000 m and r = 6,371,008 m . The result is d = 7.848 m .

Created by Davide Borchia

Davide Borchia

Physicist by education, scientist by vocation. He holds a master’s degree in complex systems physics with a specialization in quantum technologies. If he is not reading something, he is outdoors trying to enjoy every bit of nature around him. He uses his memory as an advantage, and everything you will read from him contains at least one “I read about this five years ago” moment! See full profile

Check our editorial policy

Reviewed by Steven Wooding

Steven Wooding

Physicist holding a 1st class degree and a member of the Institute of Physics. Creator of the UK vaccine queue calculator, and featured in many publications, including The Sun, Daily Mail, Express, and Independent. Tenacious in researching answers to questions and has an affection for coding. Hobbies include cycling, walking, and birdwatching. You can find him on Twitter @OmniSteve. See full profile

Check our editorial policy

New

Table of contents

What is the horizon?How do you calculate the distance to the horizon: formula and explanation Example of calculations of the distance to the horizon How to use our distance to horizon calculator FAQs

Our distance to horizon calculator tells you how far you can see from any height above Earth (or any other planet). Keep reading to discover more about the topic. In this article, you can learn the following:

What is the horizon?
How do I calculate the distance to the horizon from the height?
Example of using the formula to calculate the distance to the horizon at sea level (on Earth and other planets).

And much more!

What is the horizon?

The horizon is the apparent division between the sky and the ground as viewed from the perspective of an observation close to the surface of a planet or other celestial body (or, if we scale things down, any kind of spherical object much bigger than the observer).

The horizon is well defined, mathematically, only if there are no obstacles, that is, if your line of view is clear. The best situation for this happens when you are on the seashore, facing the open sea. If trees, buildings, hills, or other geographical features lie before you, they may cover your horizon.

How do you calculate the distance to the horizon: formula and explanation

To calculate the distance to the horizon $d$ , you need to know only two geometric parameters:

The radius of the planet/object you are considering in your distance to horizon calculations ( $r$ ); and
The height of the observer above the surface ( $h$ ).

Once you know these quantities, we can build a geometric construction to understand the following steps to find the formula for the distance to the horizon.

Draw the line connecting the center of the body to the observer's "feet". This line has length $r$ .
Extend this line to the point from which the observer is looking ( $h$ ).
Sum these two segments: the resulting one will have length $r+h$ .
Draw the tangent from the observer's point of view and the surface of the body.
Connect the point where the tangent touches the body to the center. These two last segments form a right triangle.

You can see this construction in the graphics below.

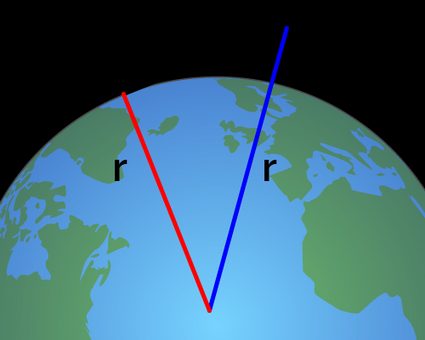
By building a right triangle with the right angle centered in the observer's feet, we can calculate the distance to the horizon.

🙋 Visit our right triangle calculator and special right triangles calculator to find out more about this ubiquitous shape!

You know the hypotenuse of the triangle ( $r+h$ ) and the longer cathetus ( $r$ ). The distance to the horizon is shorter one.

The formula to calculate the distance to the horizon uses Pythagora's theorem:

d = \sqrt{(r+h)^2-r^2}

Example of calculations of the distance to the horizon

What is the distance to the horizon on Earth? Assuming the observer's height to be an average $h = 1.75 \ \mathrm{m}$ , we can easily find the result.

Let's find the other value we need to know before calculating the distance to the horizon: Earth's radius. Scientists made a reasonably accurate estimate at $r = 6,\!371,\!008\ \mathrm{m}$ (remember that Earth is not a sphere, but more of an ellipsoid, or even better, a geoid: these differences don't change the result by a lot, but we implemented it in our great circle calculator).

Now plug these values in the formula for the distance to the horizon:

\begin{split} d &= \sqrt{(r+h)^2-r^2}\\[.5em] &= \left( (6,\!371,\!008\ \mathrm{m} + 1.75\ \mathrm{m})^2\right.\\ &\qquad\left. - (6,\!371,\!008\ \mathrm{m})^2\right)\\[.5em] &=4,\!722\ \mathrm{m}\approx 4.7\ \mathrm{km} \end{split}

How far would you see if you were on the (hypothetical) surface of Jupiter, the largest planet in the Solar System? Simply change the value of the radius. The formulas become:

\begin{split} d &= \sqrt{(r+h)^2-r^2}\\[.5em] &= \left( (69,\!911,\!000\ \mathrm{m} + 1.75\ \mathrm{m})^2\right.\\ &\qquad \left. - (69,\!911,\!000\ \mathrm{m})^2\right)\\[.5em] &=15,\!643\ \mathrm{m}\approx 15.6\ \mathrm{km} \end{split}

More than three times the previous result. How far would the horizon be on Mars, then? Discover it with our distance to the horizon calculator!

How to use our distance to horizon calculator

Our tool implements a simple formula to calculate the distance to the horizon from a height. The only required input is the height of the observer. Try it with your height to check the distance of your horizon at sea level.

If you are curious about horizons on other planets or moons, change from Earth to any other body in the list or select Enter a custom radius to be able to insert any value of the radius (you can even simulate the horizon of an ant on a basketball ball, for example).

🙋 For a more specific tool, head to our Earth curvature calculator! 🌍🌎🌏

FAQs

How far would I see on the Moon?

The horizon for an average human 1.75 m tall would be about 2.5 km. As the Moon is smaller than Earth, the horizon on our satellite would be closer than Earth's. To compute the distance of the horizon on the Moon, follow these easy steps:

Sum the radius of the Moon and your height, and compute the square of the result: (1,737,500 + 1.75)².
Subtract the result to the square of the Moon's radius: 1,737,500².
Take the square root of the result:

√((1,737,500 + 1.75)² - 1,737,500²) = 2,466 m ≈ 2.5 km.

How do you calculate the distance to the horizon?

To compute the distance to the horizon, we follow these easy steps:

Compute the sum of the radius of Earth and the height of the observer.
Calculate the square of Earth's radius.
Subtract the result of step 2. from the result of step 1., and take the square root.
The result is the distance to the horizon. We calculated it using Pythagoras' theorem on a right triangle with corners in the center of Earth, the observer, and the horizon.

What is the distance to the horizon if I'm 1.75 m tall?

On Earth, with an unobstructed view, the distance to the horizon calculated for a height of 1.75 m would be approximately 4.7 km. To find this result, use the formula for the distance to the horizon:

d = √((r + h)² - r²)

where:

d — Distance to the horizon;
r — Earth's radius (r = 6,371,008 m); and
h — Height of the observer (h = 1.75 m).

Substitute these values in the formula to find the result.

How high should I be to see 10 km away?

Not as high as you would imagine: 7.85 meters above the ground would be enough to see as far as ten kilometers away. We used the inverse formula for the distance to the horizon.

Start with the distance to the horizon equation: d = √((r + h)² - r²).
Rewrite it for h. You'll find a quadratic equation:

h² + 2rh - d² = 0
Take the positive root of the equation:

h = 1/2 · (-2r + √(4r² - 4d²))
Substitute d = 10,000 m and r = 6,371,008 m.

The result is d = 7.848 m.