Great Circle Calculator

Our great circle calculator will show you why you crossed the tip of Greenland while traveling from Los Angeles to London, even though it looks well out of the way. Here you will understand how maps bend reality and acquire a better grasp of aerial routes.

Take off with Omni, and discover the quirks of geodesics; keep reading to learn:

• What is the great circle?
• How many great circles are out there?
• What is the great circle distance? And much more!

We will teach you how to calculate the great circle distance between two points, both on a sphere and a more realistic shape for Earth. What are you waiting for? Get ready for departure!

We can give you two definitions of the great circle, one of them complex, albeit straightforward; the other much more intuitive. Before the definitions, though, it's better to introduce the situations in which we will test our great circle calculator!

We define great circles on solid shapes with some degrees of rotational symmetry, namely spheres and ellipsoids. On such figures, the rules of the geometry we meet every day are somehow... bent. Let's see how!

What is a great circle: a mathematical definition

The great circle is the closed circle deriving from the intersection of a sphere and a plane passing through the center of the sphere. The intersection traces the largest possible closed path on a sphere.

This definition, of course, allows you to create infinitely many great circles. The same holds if we consider the great circle passing through a point on the sphere's surface.

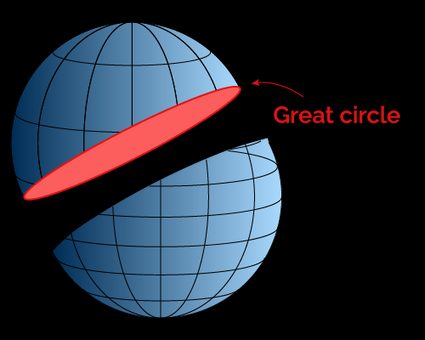
This infinite multiplicity is eventually broken when we try to find the great circle between two points. In fact, by choosing two distinct points on a sphere, you can trace a single great circle between them.

When considering two points and the great circle between them, we can define (and calculate) the distance between them on the great circle: there are two possible values:

• The longer path; and
• The shorter path.

The shorter path leads us to the second definition of the great circle.

The great circle definition based on the distance between two points

The great circle is the circle containing the shortest possible path between two points on a sphere.

Earlier, we said that the great circle distance we calculate between two points is the shortest possible path. This characteristic makes this path a geodesic of our solid. A geodesic is a particular curve that defies our common sense a bit.

As humans, we perceive our world as a set of orthogonal coordinates, and the shortest path between two points in our field of view is — if obstacles allow it — a straight line. Expand your horizon to a larger scale, and consider the planet. Take two points, and draw the shortest line across them (you can do it by wrapping a taut string around the planet — though this is more easily done on a globe). Now "open" the planet's surface to visualize it in two dimensions: we did it in the picture below.

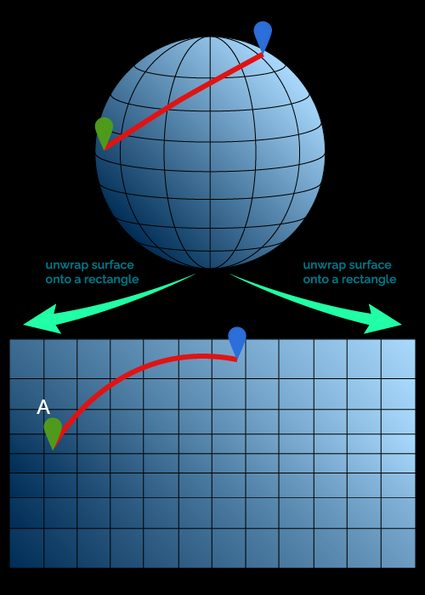
Our straight line has bent! Was it a straight line in the first place? Maybe it was just because of our vantage point? It's a complicated question, and the answer is geodesic!

Why do the geodesics on a sphere look so weird? The problem lies in the impossibility of representing truthfully such shapes in two dimensions. Have you ever tried flattening a ball? Yup, you can't unless you stretch the fabric in some way. That's what we do when we draw a map in the widespread Mercator projection: stretch the poles so much that they are apparently equal to the length of the equator — while in three dimensions, those are points: not lengths at all!

To calculate the great circle distance between two points, first, we must decide which shape we are drawing our geodesic on.
In Omni's great circle calculator, we will consider two cases:

• sphere; and
• ellipsoid.

In both situations, our starting and ending points are uniquely identified by a pair of coordinates, the latitude and the longitude:

The latitude of a point identifies the north-south direction. The poles lie at $90\degree\ \mathrm{N}$ and $90\degree\ \mathrm{S}$, while the equator lies at $0\degree$. The longitude varies from $0\degree$ (passing through Greenwich) to $180\degree$ on the other side of the globe. We mark the longitude in the two hemispheres with $\mathrm{E}$ and $\mathrm{W}$.

If you want to learn how to calculate the great circle distance between two points, we need to set a convention on the latitude: we will use trigonometric functions, and they don't like "west" or "north" as quantities. The convention we use is the following:

• For points in the northern hemisphere, the latitude is positive;
• For points in the southern hemisphere, the latitude is negative;
• The longitude of points in the eastern hemisphere is positive: and
• The longitude of points in the western hemispheres is negative.

How to calculate the great circle distance on a sphere?

Let's see, now, the relatively easy case of a sphere! Take two points, $A = (\varphi_\mathrm{A},\lambda_\mathrm{A})$ and $B = (\varphi_\mathrm{B},\lambda_\mathrm{B})$. To calculate the shortest path on the great circle, use the formula:

Where $r$ is the radius of your sphere (or ideal planet). The formula rightfully reminds us of the one we use to calculate the circumference of a circle, $C = r\cdot2\pi$. There, you take the radius $r$ and multiply it by the full angle (the one defining a circle!). In the case of the great circle distance, we are still considering a circle with radius $r$, but a different central angle (as we can see in the arc length calculator).

How to find the other great circle distance between the two points? Simply subtract the argument of the inverse cosine from $360\degree$ (or $2\pi$, if you are working using radians). Equivalently, subtract the length we previously found from the circumference:

How to calculate the great circle distance on an ellipsoid

The real world hits us hard when it comes to calculating the great circle distance between airports or any pair of points on a planet. See, planets have the annoying habit of being larger at the waist; technically, we call this phenomenon "equatorial bulge", which originates because a planet spins relatively fast around its axis, with maximum speed at the equator corresponding to higher (although apparent) centripetal force. From an ideal sphere, we have then to consider an ellipsoid.

To calculate the great circle distance on an ellipsoid, we need to know a couple of parameters:

• $a$ — The semi-major axis;
• $b$ — The semi-minor axis; and
• $f$ — The flattening of the ellipsoid.

The numerical values of these quantities, at least for the Earth, come from a reference ellipsoid model. In our great circle calculator, we went for the WGS 84: a widespread model used even by GPS satellites. Here are the numbers:

• $a = 6 378 137.8\ \mathrm{m}$;
• $b \approx 6 356 752.314140\ \mathrm{m}$; and
• $f = 298.257 223 563$.

We will now introduce Vincenty's formula to calculate the great circle on an ellipsoid. First, define the following quantities:

• The reduced latitude of the points:
  • $\small U_\mathrm{A}\! =\! \mathrm{arctan}\!\left((1\!-\!f)\tan(\varphi_{\mathrm{A}})\right)$; and
  • $\small U_\mathrm{B} = \mathrm{arctan}\!\left((1\!-\!f)\tan(\varphi_{\mathrm{B}})\right)$.
• The difference in latitude on the auxiliary sphere, $\lambda$. We set this value, at the beginning of our calculations, to the difference in latitude $L$: $\lambda = L = \lambda_{\mathrm{A}} - \lambda_\mathrm{B}$. You will need this quantity later!

In our calculations, we will make use of two other angles:

• $\sigma$ — The angle between the two points; and
• $\sigma_{\mathrm{m}}$ — The angle between the midpoint of the great circle distance and the equator.

In the first steps of our calculations, we iterate a set of operations until their result ($\lambda$) converges to the desired accuracy.
The first equations define the sine and cosine of the (unknown) angle $\sigma$ between the points:

And:

We then find the value of the angle with the function $\mathrm{arctan2}$, which computes the angle between the horizontal axis and the segment between the origin and the point identified by the argument, thus removing the uncertainty associated with the arctangent function (you can learn more about this trigonometric function at our arctan calculator). The angle $\sigma$ is:

Proceed to compute the angle $\alpha$ (this quantity is a bit more complex to explain):

This quantity is necessary in the calculations for $\sigma_\mathrm{m}$, and roughly coincides with the angle of the geodesic compared to the equator. Next step:

Now, with this quantity, we compute the value of the temporary variable $C$:

And finally, we calculate the new value of $\lambda$:

where

Now compare the value of $\lambda$ we set at the beginning and the one we found with the last step: $\lambda_{\mathrm{new}}$. Their difference has a given value, and our objective is to minimize it (or at least, reduce it).

Set a threshold, say $10^{-12}$, and repeat the steps above till the difference $\lambda-\lambda_{\mathrm{new}}$. Every time you start again, perform the substitution $\lambda = \lambda_{\mathrm{new}}$.

And now we need to calculate the great circle distance between two points on an ellipsoid. Start by calculating the following equation:

Next steps, find the values of $A$ and $B$:

where

And:

with

Now calculate the angle covered by the path. You're warned, it's not a nice formula:

We're on it! Using (some) of the quantities we found before, we calculate the great circle distance:

You may think that all these formulas and math are out of this world and live only in textbooks. Where can we use the calculations for the great circle distance between two points? Well, we're glad you asked!

Every time you take a plane for more than a regional flight, your route would not follow a straight line on the map, but rather a geodesic. Use our tool to calculate the great circle distance between airports: we set the default values to the ones of the Los Angeles airport and Heathrow. Their coordinates are:

And:

Before applying the great circle distance calculation formulas, convert the angles to radians. You can use our angle conversion for the purpose! Showing off the entire procedure for Vincenty's formula would be tiresome, let's only check the solutions for this aerial route:

As you can see, the difference is not dramatic, falling short of $0.25\%$ of the longer one. On a map, it would be barely noticeable. In blue, you can see the great circle route between Los Angeles airport and Heathrow airport: see how it passes way higher than you'd expect.

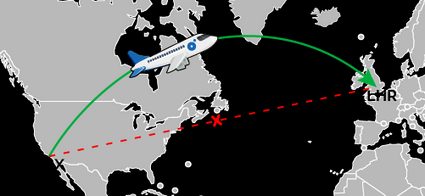
The difference between the distances changes significantly if we measure the length of the apparently straight path in red. By using the good old Pythagorean theorem on the "horizontal" and "vertical" distances between airports, we can compute the non-geodesic distance between the two airports: it would amount to more than $10000\ \mathrm{km}$. Yup, better passing over Greenland!

Last, but not least, jump on a rocket, and look at our Planet from above. The geodesic would look exactly like a straight line from a specific point above the northern hemisphere, confirming that it's effectively the shortest path!

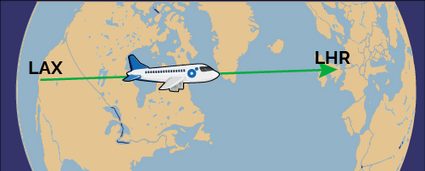
This is only but an example of calculations of the great circle distance. Have fun with our calculator; it's straightforward to use!

One last fun fact: if you've seen a sci-fi movie, you likely noticed those nice-looking screens with the paths of satellites above Earth. Those often are geodesics, great circles! Look at the picture below.

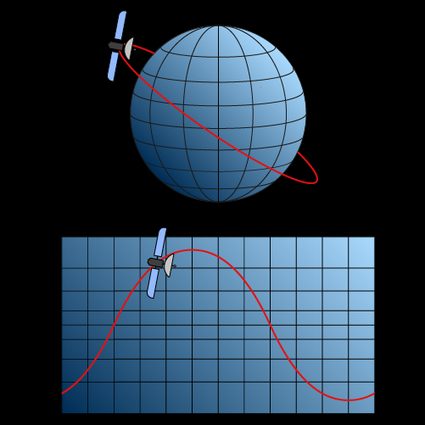
Not only can we see that a circular orbit follows the rules of geodesics, but that the "bends" change direction when you cross the equator: geodesics are even weirder than we already knew!