Daylight Calculator

Use our daylight calculator to find out how many hours of daylight you will have in the summer, particularly if you are tired of those short and dark days in the winter.

In this article, you will learn:

• How to calculate daylight hours for any location on Earth (almost!);
• How do the hours of daylight depend on the latitude;
• Some facts on the duration of the day across the Planet;
• and much more!

Jump onboard and discover the science of bright, long days with Omni!

Daylight is the portion of the day when the Sun shines on a defined location. Clouds don't count, and even if you were inside, the Sun was above you. According to this definition, daylight is the time that runs between sunrise and sunset. Counting daylight is a pretty straightforward operation: you just need to know the time of the local dawn and twilight and count the hours in between.

Did you know that the effective length of daylight is slightly more than the math suggests to us? The effect of atmospheric refraction, which bends the light rays coming from the Sun in the early and late phases of the day, gives us some minutes of extra Sun every day! We will learn the math behind this phenomenon in the next section.

To calculate the hours of daylight from the latitude, we need to perform a certain number of length calculations to find the time of sunrise and sunset. To do so, we need to know the latitude ($\phi$) and longitude ($\lambda$) of a place on Earth. To calculate the daylight hours for a specific day of the year, we also need to know the day number $n$ ($1$ for the first of January, and so on).

A bit of rather boring math follows: we will write down the steps and comment on them, but they are relatively advanced. You may also find alternative formulas on the Internet: we choose the ones that resulted in the most accurate results, even though they may not be so straightforward in their derivation. Let's start!

Since latitude is expressed in degrees, but we instead prefer to measure time, we apply a weird conversion between angle and time:

We then find an approximation of the local sunrise and sunset time. Mathematicians call this step "ansatz": an educated guess. In our case, we assume that the sun rises at 6 local time, and sets at 18. Reasonable, right?

In the following steps, we will use a generic $t$ to mark the previously found quantities: for a while, it won't make a difference. We'll let you know when to remember about them!

We find the Sun's mean anomaly, a measure of how much the Earth's elliptic orbit overshoots the circular orbit with the same period (we taught you how to calculate this quantity at the orbital period calculator).

Next, we need to find the coordinates of the Sun in the sky: instead of latitude and longitude, we calculate the declination $\delta$ and right ascension $\mathrm{RA}$.

To find them, we need first to compute the Sun's true latitude:

Calculate $L\mod\ 360\degree$ to ensure that the angle falls in the correct range, $[0\degree,360\degree)$.

For the right ascension:

To make sure that we aligned our coordinates correctly, we check that the true latitude and right ascension fall in the same quadrant of the sky by tuning the latter's value:

And use these values to calculate the "updated" right ascension:

We calculate the Sun's declination, the other coordinate of our Star, according to Earth's reference frame. We directly find the value of its trigonometric functions.

Then, we find the value of the Sun's local hour angle: this quantity describes the angular position of our star according to the local zenith (the point right above your head):

Notice that the fraction is not necessarily in the "legal" bounds: we can meet two conditions, with the cosine of $h_\mathrm{a}$ never rising ($\cos(h_\mathrm{a})>1$) or never setting ($\cos(h_\mathrm{a})<-1$). When the value of the cosine is outside of the range, we have full days of sunlight or darkness.

The angle $z$ is the angle of the Sun relative to the zenith. For the "true" sunrise and sunset, it equals $90\degree$. We'll see later the values it can assume.

Interlude: how the atmosphere bends light and fights the night

If you want to know the effective length of daylight, you need to consider the refraction of the Sun's rays due to the atmosphere. At sunrise and sunset, the light from the Sun must cross a thicker layer of atmosphere to reach you. The atmosphere has a variable index of refraction, which depends on the density.

Thanks to Snell's law (we explained it thoroughly at the Snell's law calculator), this results in a change in the angle with which the rays cross the atmosphere. At sunrise and sunset, this deflection reaches up to $0.5\degree$.

Considering the Sun's diameter instead of its center, we can reach a correction of $\small 0.833\degree$ to our sunrise/sunset angle, marking effectively the first moment the Sun pokes above the horizon (or when it completely disappears below it). Plug this correction in the formula above by setting:

Now we can convert the hour angle into hours. Remember that we can calculate two values for the hour angle: one using $t_\mathrm{rise}$ for the sunrise, and the other ($t_\mathrm{set}$) for the sunset. Depending on what phenomenon we are considering, we find the hour angle using the inverse cosine in the following equations:

Convert this angle in hours using the conversion we saw a while ago:

We're all set: the UTC time for the phenomenon is, in both cases:

where $t$ can be either $t_\mathrm{rise}$ or $t_\mathrm{set}$.

The last passage of our calculations for the hour of sunset and sunlight involves returning the time in UTC to the local time:

If this value is outside the range $(0,24]$, adjust it with the modulo operation. Last (we swear) step: subtract the hours of the sunset and sunrise. If possible, you'll find the length of the day (there may be extreme cases). Here is the final formula, and the only one that you really must know:

We need to make a couple of remarks:

• The calculated daylight hours depend only on the latitude; they are equal for all longitudes at a fixed latitude value.

• The formula for the daylight time breaks (a bit) for latitudes above the polar circles. In these situations, we need to use the brain to decide if we are witnessing a day of sunlight or a day of darkness.

How do the daylight hours change with the latitude?

The animation below shows how the daylight hours vary during the year for all latitudes. The horizontal sections at the extremities correspond to 24 hours of sunlight or darkness. You can see how the curve oscillates around the point $(0\degree,12\ \mathrm{h})$: at the equator, every day has the same length!

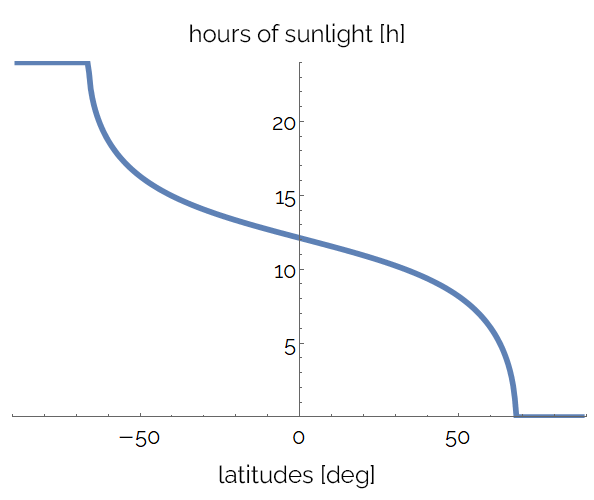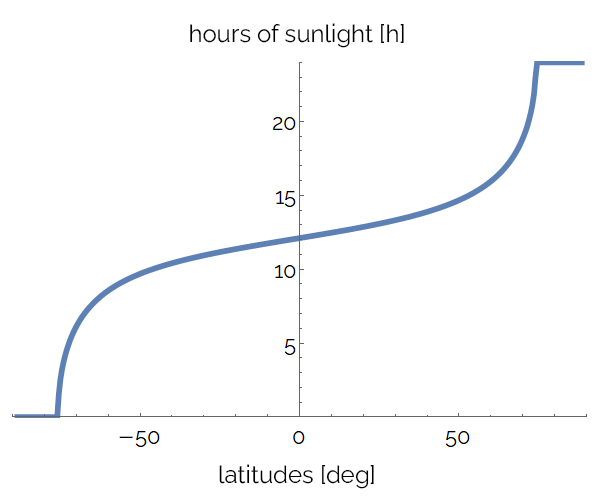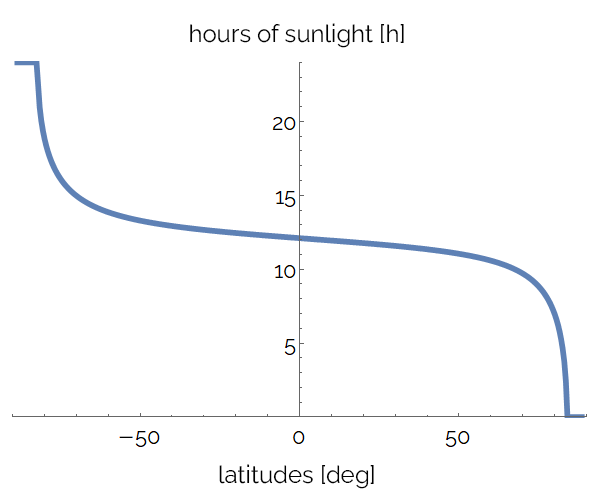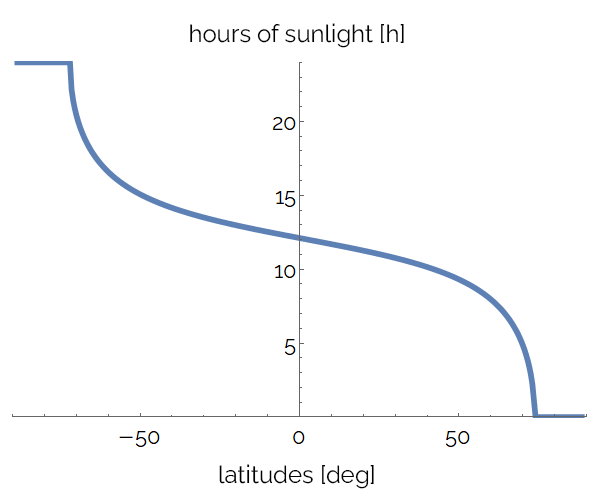
Let's fix a point on the horizontal axis. We can see how the daylight hours vary for a specific location: the following image represents the daylight hours across an entire year for the Australian city of Gold Coast.

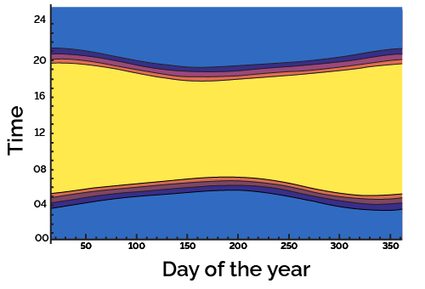
Since Gold Coast lies in the southern hemisphere, the shortest duration of the day falls in June: in Australia, Christmas doesn't equal snow! Did you notice the colored bands above and below the yellow section representing the daylight hours? Those are the warm hues of sunrise and sunset; believe it or not, we can calculate them!

We can add some complexity by considering the different (and visually distinct) phases of sunrise and sunset: the stages correspond to three angles below the horizon:

• Astronomical dawn/twilight – $18\degree$ to $12\degree$ below the horizon;
• Nautical dawn/twilight – $12\degree$ to $6\degree$ below the horizon; and
• Civil dawn/twilight – $6\degree$ to the horizon.

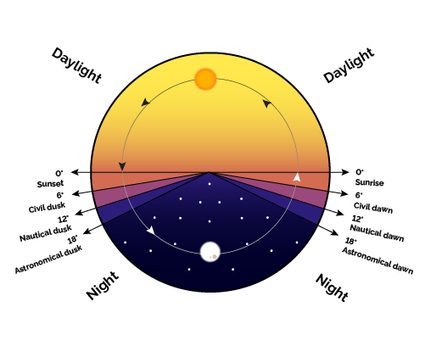
The duration of the various phases depends on the latitude and the day of the year, but generally, it is longer for higher latitudes. The picture below represents the subdivision of a mid-March day in Gold Coast.

As you can see, the three phases of sunrise and sunset take place in maybe an hour or two. Move to the other side of the globe: we choose the Russian city of Murmansk. There, in mid-March, the daylight hours almost equal the one in Gold Coast, but look at civil, nautical, and astronomical sunrises and sunsets.

They last from the small hours of the night to dawn and from sunset to late in the evening: the night in its darkest form last a mere couple of hour! If you visit a place in the higher latitudes, you may witness almost endless sunrises and sunsets.

Calculating the daylight hours shows how much this quantity varies across latitudes: in this section, we will explain why and give you some examples.

First on the list, we meet a city at the middlemost of the middle latitudes: Rome (but also Chicago, New York, Tbilisi, Sapporo, and Barcelona: only the latitude matters!)

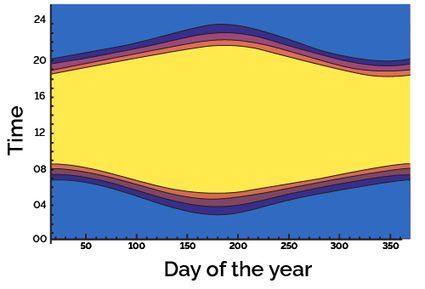
The amount of daylight we calculate depends on the latitude of the location only. This quantity tells us how much the position of the Sun changes in the sky during the year.

For a place close to the equator, the Sun's position oscillates mildly by only $\pm23.44\degree$ from the zenith. The variations in daylight hours are negligible, and you get a climate devoid of seasons dependent on the position of the Earth in its orbit.

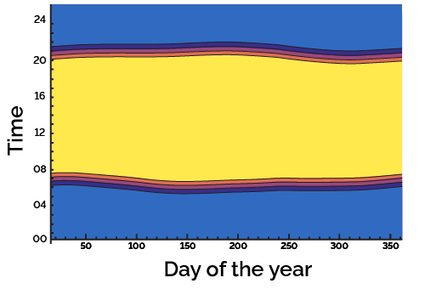
On the other extreme, you get locations above the polar circles. At those latitudes, there are days of the year when the Sun never sets and, six months later, never rises. There, you can experience the midnight sun (or a midday night, though fewer people are interested in this one). In the picture below, you can see the amount of daylight calculated for the charming town of Tromsø in Norway.

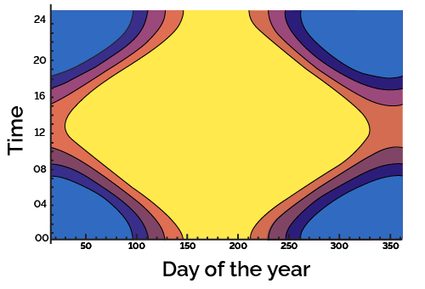
This image clearly shows that in the summer, you need very dark curtains if you want to sleep there: for a couple of months, the Sun never dips entirely below the horizon. On the other hand... there is never a 24-hour long night: even during the winter solstice, you would still get some light during the four hours long civil sunset.

To see the most authentic example of a long night, we present you with the same diagram for the North Pole (to be honest, a location a degree south of it, at $89\degree$ north).

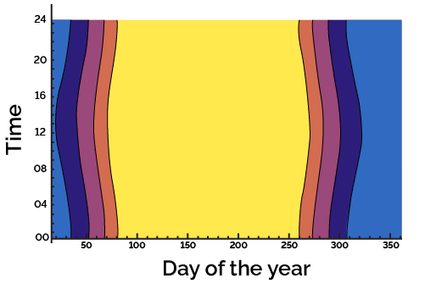
Now it's clear! If you remember how to read this type of diagram, you will quickly notice that at the poles, the Sun doesn't change height in the sky on the days. The boundary between daylight (yellow) and twilight (orange) happens two times at the equinoxes. On those days, the Sun hovers midway across the horizon, neither rising nor setting. For all the other days, the Sun is either over or below the horizon for 24 hours. Here, for a couple of months a year, you would not even know about the existence of the Sun apart from the magnificent northern (or southern) lights!

The key to these dramatic changes in the duration of the hours of sunlight lies in the angle of the Sun's path in the sky. In the next image, you can see how the Sun moves in the sky during the solstices and the equinoxes for three localities: the mid-latitudes, a location above the polar circle, and on the equator.

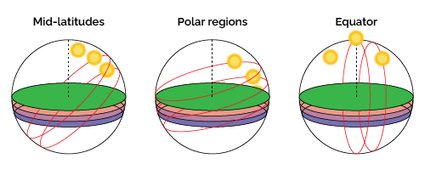
You can see so many things here! We will only point out some of them; feel free to explore the rest!

• The Sun is at its highest angle over the horizon on the equator. The opposite is true for polar latitudes.

• However, since the angle of the path of the Sun is more horizontal at the poles, the Sun, during the summer solstice, spends much more time over the horizon.

• Low angle means low energy: this is why there is ice at the poles even though the Sun is out for 24 hours (and also why you can't grow tomatoes in the Nordic countries, even though in the summer the Sun is out for ages!).

• In the polar regions, the Sun needs more time to cross each phase of the sunrise and sunset: this is why dawn and twilight are longer at higher latitudes!

To calculate the hours of daylight, we had to find the times of sunrise and sunset: you can learn how to do it with Omni's tools:

• The sunrise calculator; and
• The sunset calculator!

To calculate the length of the daylight hours, you need to follow some simple steps:

1. Find the time of the local sunrise t(rise).

2. Find the time of the local sunset t(set).

3. Subtract the two values. It may be convenient to convert the time in hh:mm to decimal hours (for example, 18:30 → 18.5). The result is the length of the daylight:
   t(daylight) = t(set) - t(rise)

4. Convert back to the desired format if necessary.

Yes. In the regions above the polar circles, there is at least a day when the Sun never sets. This happens starting from the local spring equinox at the pole.

At the poles, the six months between the spring and the autumn equinox never see a sunset, while on the polar circles, only a day during the summer solstices has the famous midnight sun.

The angle of the sunrays remains low, regardless of the time spent by the Sun over the horizon: this contributes to the cold temperatures at high latitudes.

The sunset is longer at the higher latitudes since the lower angle of the Sun's path relative to the horizon causes sunrays to cross the regions right below the horizon for a more extended period of time. The thicker atmosphere (due to perspective) is the reason for warmer, reddish-orangish hues. At latitudes high enough, you may witness day-long sunrises and sunsets!

During the equinox, you will receive slightly more than 12 hours of sunlight, regardless of your position on the Planet. On those days, the Sun changes hemispheres and everywhere on the Earth; it rises and sets exactly in the east and west and takes 12 hours to cross the sky.

Due to atmospheric refraction, however, you would receive a "late" image of the Sun, even when it is under the horizon. This would give you around 15 minutes of sunlight more for the mid-latitudes!