Last updated: Jul 29, 2024

Snell's Law Calculator

Q: What is Snell's law?

Snell's law , or the law of refraction , describes the relationship between the angles of incidence θ₁ and refraction θ₂ and the refractive indices ( n ₁, n ₂) of two media: n ₁sin(θ₁) = n ₂sin(θ₂). The law of refraction allows us to predict the amount of bend when light travels from one medium to another .

Q: Does Snell's law apply to all waves?

Yes , you can apply Snell's law to all isotropic materials , in all phases of matter . This happens because Snell's law is related only to the propagation of the wave and not to the details of the wave itself. Therefore, it works for sound waves as well.

Q: What will be the angle of refraction if the angle of incidence is 10°??

7.5° . Let's say a light beam enters the water at 10° . To find an angle of refraction: Find the refractive indices of air, n ₁ =1, and water, n ₂ = 1.33. Solve Snell's law equation for θ₂: sin(θ₂) = n ₁sin(θ₁)/ n ₂. Therefore, θ₂ = arcsin(1×sin(10°)/1.33) = 7.5°.

Q: How can I calculate the refractive index of the glass using Snell's law?

Assuming that light travels from air to glass , the angle of incidence is 30°, and the angle of refraction is 20°. To calculate the refractive index, follow these steps: Identify the refractive index of air: n ₁ = 1. Modify Snell's law to find the refractive index of glass: n ₂ = n ₁sin(θ₁)/sin(θ₂). Enter data : n ₂ = 1×sin(30°)/sin(20°) = 1.46.

Q: What are the limitations of Snell's law?

The limitation of Snell's law of refraction is when light falls on the surface of the separation of two media normally or through a normal (perpendicular line). This is because when light falls through the normal, the angle of incidence θ₁ is equal to zero . Hence from Snell's law, sin(θ₁) = sin(0°) = 0 , and the angle of refraction is also equal to zero .

New

Table of contents

Snell's law of refraction Finding the angle of refraction - an example Critical angle formula FAQs

When light travels from one medium to another, it bends or refracts. The Snell's law calculator lets you explore this topic in detail and understand the principles of refraction. Read on to discover how Snell's law of refraction is formulated and what equation will let you calculate the angle of refraction. The last part of this article is devoted to the critical angle formula and definition.

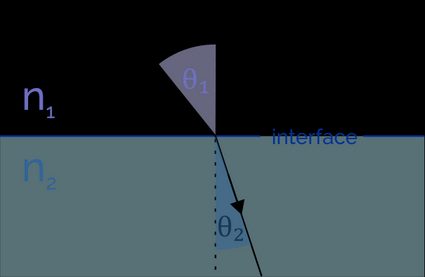
Snell's law of refraction

Snell's law describes how exactly refraction works. When a light ray enters a different medium, its speed and wavelength change. The ray bends either towards the normal of two media boundaries (when its speed decreases) or away from it (when its speed increases). The angle of refraction depends on the indices of refraction of both media:

n_1 \sin(\theta_1) = n_2 \sin(\theta_2)

where:

$n_1$ is the refractive index of medium 1 (from which the ray travels);
$n_2$ is the refractive index of medium 2 (into which the ray travels);
$\theta_1$ is the angle of incidence - the angle between a line normal (perpendicular) to the boundary between two media and the incoming ray;
$\theta_2$ is the angle of refraction - the angle between the normal to the boundary and the ray traveling through medium 2.

🔎 You can check how the speed of light can change in different media in the wave velocity calculator.

You can find some of the values of $n_1$ and $n_2$ for common media in the index of refraction calculator.

Generally, Snell's law of refraction is only valid for isotropic media. In anisotropic ones, such as crystals, the ray may be split into two rays.

Finding the angle of refraction - an example

Let's assume you want to find the angle of refraction of a light beam that travels from air to glass. The angle of incidence is 30°.

Find the index of refraction of air. It is equal to $1.000293$ .
Find the index of refraction of glass. Let's assume it is equal to $1.50$ .
Transform the equation so that the unknown (angle of refraction) is on the left-hand side: $\sin(\theta_2) = \frac{n_1 \sin(\theta_1)}{n_2}$ .
Perform the calculations: $\sin(\theta_2) = \frac{1.000293 \sin(30\degree)}{1.50} = 0.333$ .
Find the arcsin of this value: $\theta_2 = \arcsin(0.333) = 19.48 \degree$ .
You can also save yourself some time and simply use the Snell's law calculator.

Critical angle formula

Sometimes while applying the Snell's law of refraction, you will receive the $\sin(\theta_2)$ as a value greater than 1. This is, of course, impossible. If this happens, it means that all light is reflected from the boundary (this phenomenon is known as the total internal reflection). Our Snell's law calculator will advise you when this happens.

The highest angle of incidence, for which the light is not reflected, is called the critical angle. The refracted ray travels along the boundary between both media. It means that the angle of refraction is equal to 90°. Hence, you can find the critical angle by using the following equation:

n_1 \sin(\theta_1) = n_2 \sin(\theta_2)

After simplification, $n_1 \sin(\theta_1) = n_2 \cdot 1$ .

Solving for the angle of incidence, $\theta_1 = \arcsin(\frac{n_2}{n_1})$ .

🙋 Thirsty for more knowledge? Check our De Broglie wavelength calculator to read about the wave-particle duality, which explains light refraction.

FAQs

What is Snell's law?

Snell's law, or the law of refraction, describes the relationship between the angles of incidence θ₁ and refraction θ₂ and the refractive indices (n₁, n₂) of two media:
n₁sin(θ₁) = n₂sin(θ₂).
The law of refraction allows us to predict the amount of bend when light travels from one medium to another.

Does Snell's law apply to all waves?

Yes, you can apply Snell's law to all isotropic materials, in all phases of matter. This happens because Snell's law is related only to the propagation of the wave and not to the details of the wave itself. Therefore, it works for sound waves as well.

What will be the angle of refraction if the angle of incidence is 10°??

7.5°. Let's say a light beam enters the water at 10°. To find an angle of refraction:

Find the refractive indices of air, n₁ =1, and water, n₂ = 1.33.
Solve Snell's law equation for θ₂: sin(θ₂) = n₁sin(θ₁)/n₂.
Therefore, θ₂ = arcsin(1×sin(10°)/1.33) = 7.5°.

How can I calculate the refractive index of the glass using Snell's law?

Assuming that light travels from air to glass, the angle of incidence is 30°, and the angle of refraction is 20°. To calculate the refractive index, follow these steps:

Identify the refractive index of air: n₁ = 1.
Modify Snell's law to find the refractive index of glass: n₂ = n₁sin(θ₁)/sin(θ₂).
Enter data: n₂ = 1×sin(30°)/sin(20°) = 1.46.

What are the limitations of Snell's law?

The limitation of Snell's law of refraction is when light falls on the surface of the separation of two media normally or through a normal (perpendicular line). This is because when light falls through the normal, the angle of incidence θ₁ is equal to zero. Hence from Snell's law, sin(θ₁) = sin(0°) = 0, and the angle of refraction is also equal to zero.