Sunrise Calculator

Depending on the time of the year (and when you wake up), you may witness the beautiful colors of sunrise: learn how to calculate the sunrise hour, and never miss the first light of the day... if the sunrise happens!

Reading our short text, you will learn:

• What is sunrise, and what are the types of dawn?

• How to calculate the sunrise time for (almost) every location on Earth.

• How do we get some more minutes of sunlight every day thanks to the atmosphere?

• Some examples.

And much more! Wait no more, and learn this bit of astronomical geography with Omni!

Sunrise is, by definition, the moment of the day when the Sun crosses the eastern horizon and the day begins. It's not that easy, however, since sunrise is not an on-off phenomenon.

First, let's define sunrise: the sunrise time we will calculate in this tool is the time at which the upper edge of the solar disk touches the horizon. Before that moment, and for a while, you could already see the sky being pretty bright, and, to be honest, it was even an hour or so before you could tell that it was not night anymore.

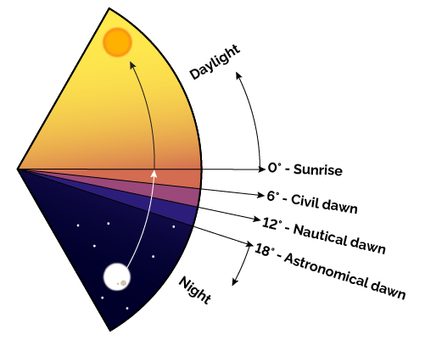
Geographers, astronomers, sailors, and some other professionals divide dawn into three phases, according to the angle of the Sun below the horizon:

• If the Sun lies between the horizon ($0\degree$) and $6\degree$ below it, we identify the civil sunset. Street lights are not necessary, and your day can start without feeling it's too early!

• When the Sun is between $6\degree$ and $12\degree$, you can still see a couple of bright stars in the sky, but reading would be difficult. Better bring a light in this sunrise phase, the nautical sunrise.

• If you are stargazing, the time the Sun is between $12\degree$ and $18\degree$ marks the disappearance of the faintest celestial objects (nebulas and galaxies, for example). We call this phase the astronomical sunrise.

To sum up, here are the three types of dawn:

• From $18\degree$ to $12\degree$ below the horizon: astronomical sunrise;
• From $12\degree$ to $6\degree$ below the horizon: nautical sunrise; and
• From $6\degree$ to $0\degree$: civil sunrise.

To calculate the sunrise time, we need to run some calculations on a set of data that identifies a specific position in space and time. The sunrise time, in fact, depends both on the location — as the length of the day varies with the latitude and to calculate the local sunrise time, we need to know our longitude — and the date (as the days are shorter during the "colder" half of the year).

For this purpose, we ask you to know three quantities:

• $\phi$ — The latitude in degrees, positive for the northern hemisphere and negative for the southern one;

• $\lambda$ — The longitude in degrees (though we will often convert this quantity in hours), positive for the eastern hemisphere and negative for the western one; and

• $n$ — The day of the year: the number of days elapsed since the first of January (with that day numbered $1$).

We are ready to find the first quantities in our calculations for the sunset time: the approximate time of the phenomenon, $t$. $t$ is an educated guess of the local hour of the sunrise, say $6$ AM, expressed as a fraction of the year:

where $\lambda_\mathrm{h}$ is the longitude converted to hour value:

From where did we pull that $15$ value? That's the angle covered by the Sun in one hour, and since a day corresponds to $360\degree$ (approximately, but that's another story), and there are $24$ hours in a day: $360\degree/24\ \mathrm{h} = 15\mathrm{\degree/h}$.

The next passages allow you to calculate the coordinates of the Sun. To do so, we need to consider the characteristics of Earth's orbit. First, we calculate the Sun's mean anomaly, a measure of the discrepancy between an elliptic orbit and the circular orbit with an identical period:

Use the value of $M$ to calculate the true longitude of the Sun:

Use the modulo operation to ensure that this value falls in the range $(0\degree,360\degree]$.

Longitude and latitude are coordinates used on the surface of the Earth. We use a similar pair of coordinates for objects in the sky, declination and right ascension. We calculate the right ascension first:

And use the modulo operation to reduce this result to the range $(0\degree,360\degree]$. Right ascension and Sun's true longitude must fall in the same quadrants — we must align our coordinate systems. We calculate two factors using the modulo operation:

We then update the value of the right ascension:

As we did for the longitude, we can convert the value of the right ascension from degree to hour:

We are ready to calculate the declination of the Sun: this is the last step in terms of coordinates; we are not far from meeting the formula to calculate the sunrise hour. Next stop: the solar declination. To calculate this quantity, which corresponds to the angle between the Sun and the equatorial plane, we make use of the inverse trigonometric functions:

And that's it; we have all the ingredients. The only thing left to do is to calculate the hour angle, the connection between the local time and the phenomenon we are considering — in our case, the sunrise. The formula for the hour angle of the local sunrise is:

The quantity $z$ is the angle of the phenomenon from the zenith (the point of the sky right above your head). $z$ assumes different values for the various types of dawn:

• $90\degree$ for the sunrise, when the (center of the) Sun crosses the horizon;
• $96\degree$ for the civil dawn;
• $102\degree$ for the nautical dawn; and
• $108\degree$ for the astronomical dawn.

Knowing the hour angle, we can easily calculate the local sunrise time:

What we obtained here is the sunrise time in UTC (the universal time). We now need to correct it, taking into account the following:

• Local longitude;
• Time zone; and
• Daylight savings (if applicable).

The longitude appears for a pair of places in the same timezone and latitude but different longitude; the most eastward one will experience sunrise earlier than the other.

For example, on the 20^th of April, the city of Kashgar in Western China sees the sunrise at 8:12 AM. On the same day, the easternmost city in China, which shares the same timezone as Kashgar, Fuyuan, sees the Sun rise at 4:04 AM, more than four hours before!

where:

• $\lambda_{\mathrm{h}}$ — Longitude expressed in hours;
• $\mathrm{tz}$ — Local time zone; and
• $\mathrm{ds}$ — Correction due to daylight saving time: if the desired location is currently using that time, assign value $1$ to $\mathrm{dz}$, otherwise, leave it at $0$.

Use the modulo operation to reduce the value you find with the last equation to the range $(0,24]$.

The atmosphere is a cozy blanket of gas that allows us to breathe and live on Earth. One of its characteristics is that its density varies with altitude. The density of a gas, alongside other parameters, affects the index of refraction, a measure of the ability of a medium to bend a light ray: the atmosphere, as a consequence, bend continuously the Sun rays entering from space, moving them to a specific angle with respect to the original, real position of the Sun.

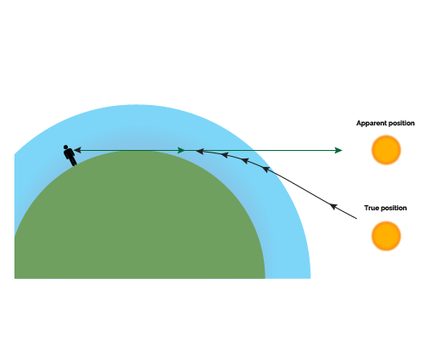
As we can learn with Snell's law (see the Snell's law calculator), the effect of refraction is higher for lower angles of incidence: the maximum deflection of Sun rays happens at sunrise and sunset. In those moments, the Sun is in a position $0.58\degree$ lower than it should; in the case of the sunrise, the consequence is that the phenomenon happens a few minutes (the amount depends on the latitude) before you'd expect. We don't complain! To make our calculations even more accurate, we add the value of the apparent radius of the Sun to this correction: the final angle is $0.833\degree$.

How do we modify the formulas to calculate the sunrise time to accommodate this modification? Take the formula for the hour angle, and substitute $z = 90+0.833\degree$:

The final result of the calculations is the time at which, on an unobstructed horizon, you'd witness the appearance of the first Sun rays of the day.

You know the sun rises early in the North, but how early? Let's calculate the time of sunrise for Rejkyavik, the capital of Iceland. We chose a place with coordinates $64.164153\ \mathrm{N}$, $22.022493\ \mathrm{W}$.

On our sunrise calculator, switch the units for the coordinates from degrees/minutes/seconds to degrees, and input the coordinates above. Remember to select the correct hemispheres!

Now set the timezone. Iceland, to be in sync with Europe, observes GMT. This is not a big deal since the day length variation at these latitudes is so huge that there is no "correct" time zone. No daylight savings; it's not needed in a country where there is barely a sunset in the summer!

Next, let's choose the day: we went for the summer solstice, the 21^st of June. The time of the sunrise is 2:55 AM! You probably won't need a flashlight.

Omni didn't stop with the sunrise calculator: below, you can find a list of other tools, more or less specific, about the different moments of the day!

• The sunrise sunset calculator;
• The sunset calculator; and
• The dayligth calculator.

Atmospheric refraction bends the light rays from the Sun by slightly more than half a degree. This bending causes the Sun to be in an apparent position higher than it is in reality. The effect is a somewhat sooner sunrise, with the upper rim of the solar disk appearing (on average) five minutes before the expected time.

The bending of light rays is accentuated at sunrise and sunset since the distance traveled in the atmosphere is longer, and the angle of incidence is higher.

The sky is pink at sunrise thanks to Rayleigh scattering: the phenomenon causes photons from the Sun's rays to disperse when they encounter gas molecules in the atmosphere.

Scattering is more intense for shorter wavelengths: that's why the sky is blue during the day. Sun rays travel longer in the atmosphere during sunset and sunrise, and blue and green wavelengths get scattered well before we can observe them. This leaves the relatively unaffected red hues to reach us, giving us the warm colors of dawn and dusk.

7:06 AM. To find this time, follow these steps:

1. Calculate the solar declination. In this case, the value is δ = -23.39°, close to its minimum value.

2. Calculate the hour angle:

   ha = (cos(90.833 - sin(δ) × sin(𝜙))/(cos(δ) × cos(𝜙)),

   where:

   • 90.833 — Angle for the sunrise, corrected for refraction; and

   • 𝜙 — The latitude.

   Then: ha = 278.73°.

3. Calculate the UTC time for the sunrise.

4. Correct the UTC time with the value of the local longitude and the time zone.

The earliest sunrises happen on the days of the solstices. There are two solstices, a summer one and a winter one. During the winter solstice, the sun rises as early as it ever does in the southern hemisphere. Those days are the longest of the year there. Conversely, the sun rises early in the northern hemisphere during the summer solstice. Those days are the peak of the summer.