Surface Area of a Rectangular Prism Calculator

Welcome to the surface area of a rectangular prism calculator, where you'll have the opportunity to learn everything about your prism quickly and easily. In particular, we'll explain how to find the surface area of a rectangular prism. Do you want to paint a barn and are wondering how much paint do I need? Or are you building a swimming pool in your backyard and want to know how many tiles you need?

No matter what the question is, as long as it boils down to "what is the surface area of a rectangular prism," you've come to the right place!

Before we see what the surface area of a rectangular prism is, we should get familiar with the prism itself.

Imagine a box. A regular, rectangular box, just like the ones you see in the supermarket, full of whatever products. Well, that is a rectangular prism! Or do you remember those drawings of houses that we did in kindergarten? Remove the angular roof, and you're left with another example of a rectangular prism.

Formally (mathematically), a right rectangular prism is a solid where all six sides are rectangles that are perpendicular to one another. Note that this, in particular, means that there are three pairs of identical faces placed on opposite sides of the solid.

Also, as with any other scientific definition, there are a few fancy names associated with the prism. The bottom and top faces of the box are called bases, and each of the other four is called a lateral face. Lastly, the sides of each rectangle are called edges (again divided into base edges and lateral edges).

Time to put the high-brow words aside and focus on how to find the surface area of a rectangular prism.

To see what is the surface area of a rectangular prism, we need to know all three of its sides. Let's start with the notation we use for them and for the other values in our surface area of a rectangular prism calculator:

• l – the first base edge length;
• w – the second base edge length;
• h – the lateral edge length (also called the height of the prism);
• A_b – the base area of the prism;
• A_l – the lateral area of the prism;
• A – the surface area of the prism; and
• V – the volume of the prism.

Note that A_b denotes the surface area of a single base of our prism. On the other hand, A_l denotes the lateral area, meaning the total area of the four lateral faces. Therefore, since the solid has two bases (the bottom one and the top one), the surface area of a rectangular prism formula is as follows:

surface_area = 2 × base_area + lateral_area,

which, in our notation, translates to

A = 2 × A_b + A_l.

Recall that all the faces in our calculator are rectangles, and, as mentioned in the rectangle area calculator, they are calculated by multiplying the side lengths. Now, let's use that information to study the base of our prism. With our notation, it is a rectangle with sides l and w, so its area is l × w. And that is precisely the formula for the base area:

A_b = l × w.

Piece of cake, wasn't it? Well, let's now try to do something a little bit more complicated and move on to the lateral area. We have four faces contributing to that number, and all of them are rectangles. What is more, among the four, there are two pairs of identical ones (the front and back wall and the left and right wall). All of those have one side equal to h, the lateral edge (or the height) of the prism. Also, the other side of one of the pairs is equal to the first base edge, say l, and the other is equal to the length of the second one, which is w. All in all, we obtain that the lateral area, or A_l as we call it, is

A_l = l × h + l × h + w × h + w × h,

or simply

A_l = 2 × l × h + 2 × w × h.

Observe that, together with the base area, this allows us to translate the surface area of a rectangular prism formula into

A = 2 × A_b + A_l = 2 × l × w + 2 × l × h + 2 × w × h.

Let's say that you're trying to tile a swimming pool and want to know the area you have to tile. If the pool is rectangular with a flat bottom, then what we're dealing with is precisely a rectangular prism! Let's look at a pretty picture to see it clearly.

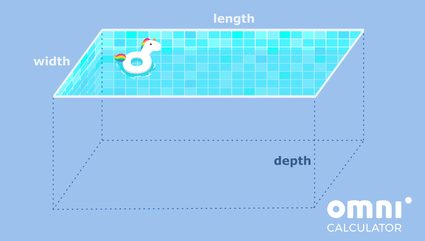
Okay, we know it's hard to keep your eyes away from the floaty unicorn, but let's get back to the problem at hand!

Say that the pool has a length of 8 feet, a width of 6 feet, and is 5-foot-deep. Now that we have the numbers let's try to put them in terms of the notation we've used above.

Firstly, the sides of the base of our pool are its length and width, which in our case are 8 ft and 6 ft, respectively. Since we're using l and w as the base edges, we can use these numbers in the calculator above and set l = 8 ft and w = 6 ft. Note that it doesn't matter in which order we put them; it only translates to looking at the pool from another angle and doesn't change its surface area.

We're left with the depth of our pool and the number h in the calculator. And that is exactly what we should do now: set h = 5 ft, which is the depth of the pool or the height of the prism.

"And we're done, aren't we?" Well, not exactly. The surface area of a rectangular prism calculator gives us the answer:

A = 2 × l × w + 2 × l × h + 2 × w × h = 2 × 8 ft × 6 ft + 2 × 8 ft × 5 ft + 2 × 6 ft × 5 ft = 236 ft².

But that is the surface area of the entire prism, and we don't want to tile it all around. After all, if we tile the top, it would be pretty difficult to get in (or out), wouldn't it? That would be some top-level malice, even worse than the removal of the ladder for your Sims.

To find the correct answer, let us move to the advanced mode. It allows us to see the base area and the lateral area of the solid. Since we know how to find the surface area of a rectangular prism, i.e., we know that

A = 2 × A_b + A_l,

we only need to subtract the extra area that we're not tiling from that. And that is the top. But the top base is the same as the bottom one, so the area we need to tile is, in fact:

tiling_area = A - A_b,

which, in our case, is:

tiling_area = 236 ft² - 48 ft² = 188 ft².

Now, that puts us one step closer to finishing the pool and being able to admire your work while drinking a cold one. That said, the prism isn't the only 3D shape with a rectangular base; find out more on the calculator for the surface area of a rectangular pyramid.