Star Shape Calculator

Twinkle, twinkle, little star... our star shape calculator will calculate all of the important elements of a star polygon in the blink of an eye!

Here you will learn everything about star-shaped polygons. Well, everything apart from occultism: we deal with geometry, not magic! Keep reading to find out:

• What are star-shaped polygons;
• How to build them;
• What is the pentagram: a down to Earth introduction;
• Other star-shaped polygons; and
• How to use our star shape calculator.

We also added some fun facts about these shapes and a challenge: how many triangles are in a pentagram? To the stars, with Omni Star Shape Calculator!

Star polygons are the shiniest shapes in geometry. By definition, they are:

• Non-convex;
• Self-intersecting;
• Equilateral; and
• Equiangular polygons.

Let's look at all of these features one by one!

• Non-convex means that you can draw a line between two points inside the star-shaped polygon that passes outside its perimeter.
• Self-intersecting means that you can build all the different star shapes starting from a regular polygon and prolonging its vertexes until the extensions cross each other.
• Equilateral signifies that all the outer sides of the star-shaped polygon have the same length (latus is the Latin for side).
• Equiangular means that all the angles lying in the same "region" are equal.

The last two attributes of the star polygons automatically qualify them as regular polygons. Of course, you can build irregular star polygons, but they would be impossible to calculate, and we are here for this!

We can uniquely identify every star polygon using the Schläfli symbol. This symbol consists of a pair of numbers in the form ${n/m}$, where:

• $n$ is the number of corners/sides of the polygon; and
• $m$ is its starriness or how many distinct boundaries you can identify around the center.

Let's see how to build a star polygon, and then this notation will be clearer!

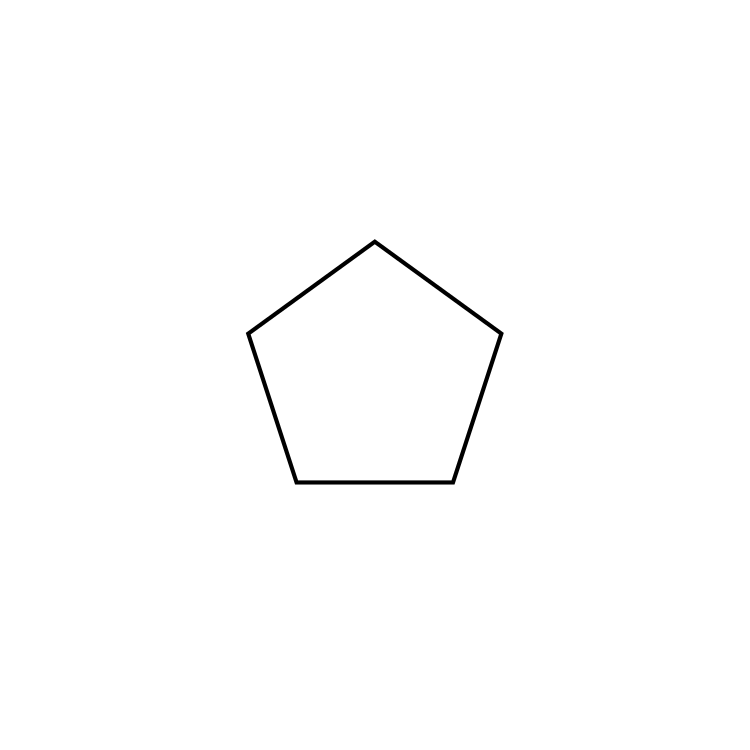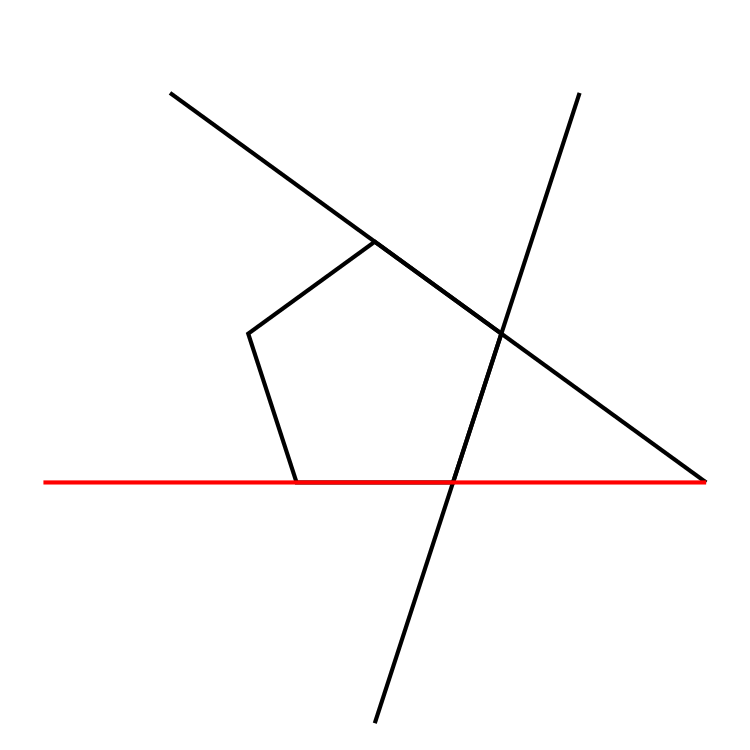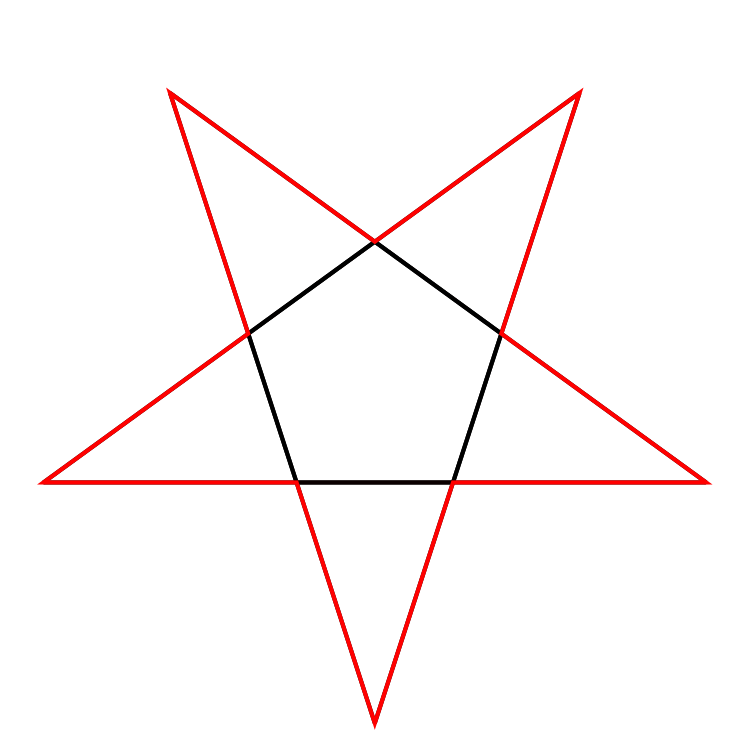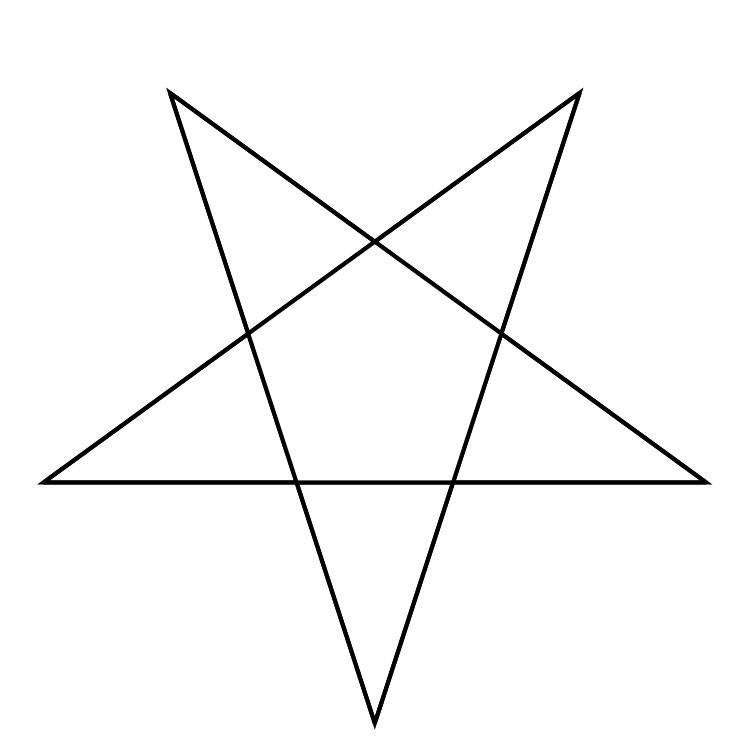
This five-pointed star polygon has the Schläfli symbol ${5/2}$, and it is so important we will deal with it in the next section.

Let's meet the VIP (very important polygon) among the star polygons: the pentagram!

What is a pentagram? The pentagram is nothing but a five-pointed star shape. However, humanity covered it with a fair dose of mysticism. It is the first regular star polygon we can build by extending the sides of a polygon (try to do that with a square or a triangle, and you will understand), and also one of the most drawn shapes in the world. In particular, you can draw it from a pentagon.

The pentagram got a bad reputation due to its association with evil: don't trust such voices and keep exploring this fascinating shape's geometry!

Here is a pentagram with all the important features highlighted!

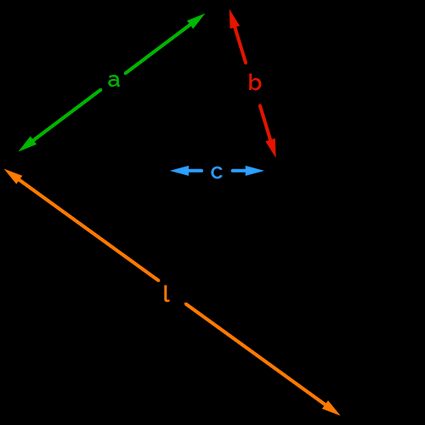
You will meet these elements in all the other star polygons in this calculator: pay attention!

You can identify:

• $a$, the distance between two contiguous "points" of the star;
• $b$, the length of the first set of "rays" wounding around the polygon;
• $c$, the side of the original polygon; and
• $l$, the distance from two "points" of the stars belonging to the same side of the polygon.

Note that connecting the points of the star creates a new $n$-sided regular polygon with side $a$!

Some relationships between those quantities always hold (for every star polygon); others are specific for a given shape. Let's check the general ones first:

• The "side" of a star is given by the sum $l=c+2\cdot b$; and
• You can calculate the perimeter of the first boundary of an $n$-pointed star with the formula:

However, there are many more "specific" formulas. Let's see the ones for the pentagram:

$\varphi$ is the golden ratio:

Only the pentagram among the star polygons has sides that relate to the ratio. Admire the proportions of these quantities:

Knowing this, we can almost understand why the pentagram got its reputation! It looks like someone really put a lot of thought into such a simple geometric shape. Learn everything about this "magic" number at the golden ratio calculator!

Apart from those golden ratios, there are a couple more relationships holding in a five-pointed star shape:

We can also calculate the value of the perimeter and the area. For the perimeter, use the general formula above, substituting $n=5$. For the area, a specific formula is needed:

Let's check out different star shapes!

If we start from the hexagon (the bestagon), we can build the hexagram. In a hexagram, we can use the following formulas to calculate the various characteristic quantities:

The factor $\sqrt{3}$ comes from the intimate connection between hexagons and equilateral triangles: the angles of such a shape are, in fact, $60\degree$ (visit Omni's equilateral triangle calculator if you want to refresh your knowledge!). When we use this value in a trigonometric function like the tangent, we find $\tan{60\degree}=\sqrt{3}$. Find out more about hexagon symmetries with our hexagon calculator.

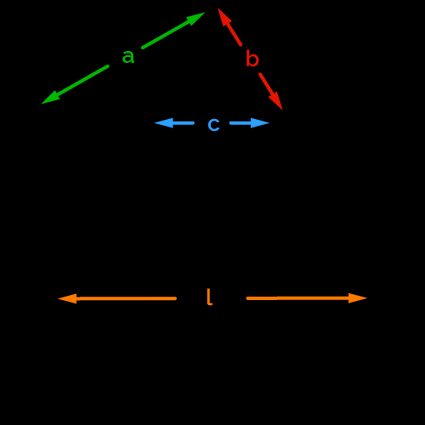
We can calculate the area of a hexagram with the formula:

Increase the number of sides and get a heptagram, a seven-pointed star. The heptagram has a particularity: it is the first star-shaped polygon for which we can naturally find a third boundary.

The reason for this peculiarity is that two sides of a heptagon separated by two others can finally meet if prolonged. In the case of a pentagram, the same couple would be a pair separated by a single side (thus a "first-order" ray), while in a hexagram, the same couple is parallel.

When drawing a heptagram then, we meet two star-shaped polygons: a stubbier one, associated with the Schläfli symbol ${7/2}$, and a more slender one with symbol ${7/3}$.

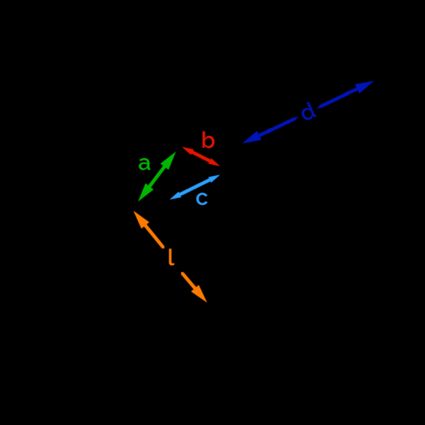
We call the side of the ${7/3}$ heptagram $d$. We can calculate the geometric relationships for both shapes, but we warn you: we will use some trigonometry, and the formulas will start to look "ugly"!

The side of the boundary ${7/3}$ comes from the formula:

The formula for the area requires we compute:

• The area of a heptagram with a side equal to $a$; and
• Seven times the area of an isosceles triangle with side $d$ and base $a$.

To conclude, the last "manageable" star-shaped polygon is the octagram, an eight-pointed star shape with an intriguing figure, rich in angles of $45\degree$. We start drawing it from an octagon, an eight-sided polygon.

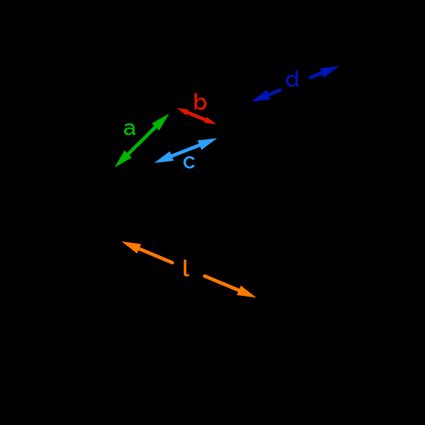
As for the heptagon, we deal with a shape with three boundaries (we can identify both ${8/2}$ and ${8/3}$). Here are the formulas for the side: don't worry if you see some $\sqrt{2}$ factors, blame trigonometry instead!

As for the heptagram, the fastest way to compute the area involves the separation of the octagram in an octagon with side $a$ and eight triangles. The formula is:

You can build star shapes for any regular polygon: the series continues with the enneagram, the decagram, etc. A generalization of the formulas is hardly helpful since every new odd-numbered polygon is associated with an additional boundary: for the enneagram, we can identify the Schläfli symbol ${9/4}$, for the hendecagram, we have the boundary ${11/5}$, and so on.

Star polygons are simple shapes, but somehow they keep appearing all around us.

Consider flags, for example. Of the $196$ country flags in the world, $40$ of them contain stars. However, the number of stars rises quickly if you count the shapes: the US flag alone contributes with 50! 😉

Burundi's and Israel's flags contain hexagrams. The flag of Jordan depicts a heptagram; the shape was also part of the old Georgian coat of arms. Only Azerbaijan contains an octagram!

Many countries have pentagrams in their flags: there is quite a constellation from the US to Somalia!

An old flag of Australia contained six-pointed stars, while the modern one has both a pentagram and some heptagrams! The designers of the national colors couldn't make up their minds!

Our favorite starred flag is the flag of Nepal: the only non-rectangular flag in the world also has a beautiful 12-pointed star which really makes it stand out!

Star-shaped polygons appear widely through sacred geometry. Do we need to mention the Star of David, a hexagram, or the shared symbolism associated with the pentagram from Hinduism to Neo-paganism?

You can also notice that the constructions of a star-shaped polygon create many triangles, the simplest bi-dimensional shape.

To make the game more entertaining, connect the outside points of the $n$-gram! How many triangles are in a pentagram shape?

We counted... $35$, how about you?

Our star shape calculator can help you calculate all of the characteristic lengths of the four most common star-shaped polygons:

• Pentagram;
• Hexagram;
• Heptagram; and
• Octagram.

Select the desired number of sides at the top of the calculator and insert the value of one of the available variables there: we will calculate all the others! For example, you can insert the area, and we will tell you all the other lengths.