Perimeter Calculator
- What is perimeter? Perimeter definition
- How to find perimeter - perimeter formulas
- Perimeter of a square formula
- Formula for the perimeter of a rectangle
- Perimeter of a triangle formula
- Perimeter of a circle formula (circumference formula)
- Perimeter of a circle sector formula
- Perimeter of an ellipse formula (ellipse circumference formula)
- Perimeter of a trapezoid formula
- Perimeter of a parallelogram formula
- Perimeter of a rhombus formula
- Perimeter of a kite formula
- Perimeter of an annulus formula
- Perimeter of a polygon formula (regular pentagon, hexagon, octagon, etc.)
With this perimeter calculator, you don't need to worry about perimeter calculations anymore. Below you'll find the perimeter formulas for twelve different shapes as well as a quick reminder about what a perimeter is and a perimeter definition. Read on, give it a try, or check this calculators twin brother - our comprehensive area calculator.
What is perimeter? Perimeter definition
Perimeter is the boundary of a closed geometric figure. It may also be defined as the outer edge of an area, simply the longest continuous line that surrounds a shape. The name itself comes from Greek perimetros: peri meaning "around" + metron, understood as "measure". As it's the length of the shape's outline, it's expressed in distance units - e.g., meters, feet, inches or miles.
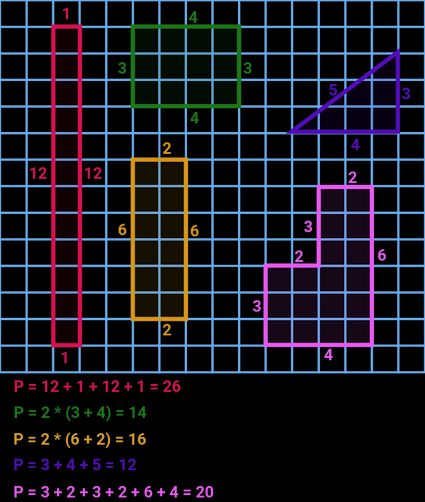
How to find perimeter - perimeter formulas
Usually the most simple and straightforward approach is to find the sum of all of the sides of a shape. However, there are cases where there are no sides (such as an ellipse, circle, etc), or one or more sides are unknown. In this paragraph, we'll list all of the equations used in this perimeter calculator. Scroll down to next sections if you're curious about a specific shape, and wish to see an explanation, derivation, and an image for each of the twelve shapes present in this calculator. We also have tools dedicated to each shape - just type the name of the shape in the search bar at the top of this webpage.
Here are the perimeter formulas for the twelve geometric shapes in this calculator:
- Square perimeter formula:
P = 4a - Rectangle perimeter formula:
P = 2(a + b) - Triangle perimeter formulas:
P = a + b + corP = a + b + √(a² + b² - 2ab * cos(γ))orP = a + (a / sin(β + γ)) * (sin(β) + sin(γ))
- Circle perimeter formula:
P = 2πr - Circle sector perimeter formula:
P = r(α + 2)(αis in radians) - Ellipse perimeter formula:
P = π(3(a + b) - √((3a + b) * (a + 3b))) - Quadrilateral / Trapezoid perimeter formula:
P = a + b + c + d - Parallelogram perimeter formulas:
P = 2(a + b)orP = 2a² + √(2e² + 2f² - 4a²)orP = 2(b + h/sin(α))
- Rhombus perimeter formulas:
P = 4aorP = 2√(e² + f²)
- Kite perimeter formula:
P = 2(a + b) - Annulus perimeter formula:
P = 2π(R + r) - Regular polygon area formula:
P = n * a
Perimeter of a square formula
A square has four sides of equal length. To calculate its perimeter, all you need to do is to multiply side length by 4:
Square Perimeter = a + a + a + a = 4a
Formula for the perimeter of a rectangle
The formula for the perimeter of a rectangle is almost as easy as the equation for the perimeter of a a square. The only difference is that we have two pairs of equal length sides:
Rectangle Perimeter = a + b + a + b = 2a + 2b = 2(a + b)
Calculating the perimeter of a rectangle is useful in all sorts of everyday situations, like, e.g., if you want to fence your plot or garden.
Perimeter of a triangle formula
The easiest formula for finding the perimeter of a triangle is - as usual - by summing all sides:
Triangle Perimeter = a + b + c
However, you aren't always given three sides. What can you do then? Well, instead of fretting, you can use the law of cosines to find the missing side:
c = √(a² + b² - 2ab * cos(γ))
This can be incorporated into the perimeter formula:
Triangle Perimeter = a + b + √(a² + b² - 2ab * cos(γ))
The other option is to use the law of sines if you have one side and the two angles that are formed by that side:
b = sin(β) * a / sin(β + γ)
c = sin(γ) * a / sin(β + γ)
so the triangle perimeter may be expressed as:
Triangle Perimeter = a + (a / sin(β + γ)) * (sin(β) + sin(γ))
Perimeter of a circle formula (circumference formula)
A perimeter of a circle has a special name - it's also known as the circumference. The most well-known perimeter of a circle formula uses only one variable - circle radius:
Circumference = 2π*r
Have you ever wondered how many times your bike wheel will rotate on a ten-mile trip? Well, that's one of the cases where you'll need to use the circumference formula. Input the radius of your wheel (half of the wheel's diameter), and divide 10 miles by the obtained circumference (but don't forget about the convert the units of length!). If you want to be even more accurate, you can include the size of the bike tire. If you're keen cyclist, don't forget to have a look at our bike cadence and speed calculator and the gear calculator.
Not convinced? Need more examples? How about calculating the icing around your circular birthday cake, or you can find how much lace you need to sew your circle skirt.
Perimeter of a circle sector formula
Calculating the perimeter of a circle sector may sound tricky - is it only the arc length or is it the arc length plus two radii? Just keep in mind perimeter definition! The sector perimeter is the sum of the lengths of all its boundaries, so it's the latter:
Circle Sector Perimeter = r * (α + 2) where α is in radians.
Perimeter of an ellipse formula (ellipse circumference formula)
Although the formula for the area of an ellipse is really simple and easy to remember, the perimeter of an ellipse formula is the most troublesome of all the equations listed here. We've chosen to implement one of the Ramanujan approximations in this perimeter calculator:
Ellipse perimeter ≈ π * [3(a + b) - √((3a + b) * (a + 3b))]
Where a is the shortest possible radius and b in the longest possible radius of an ellipse. The other, more accurate Ramanujan approximation is:
Ellipse perimeter ≈ π * (a + b) * [1 + 3(a - b)²/(a + b)²] / [10 + √(4 - 3(a - b)²/(a + b)²)]
There is also a simpler form, using an additional variable h:
h = (a - b)²/(a + b)²
Ellipse perimeter ≈ π * (a + b) * [1 + 3 * h] / [10 + √(4 - 3 * h)]
Or you could just use our calculator!
Perimeter of a trapezoid formula
If you want to calculate the perimeter of an irregular trapezoid, there's no special formula - just add all four sides:
Trapezoid perimeter = a + b + c + d
Maybe you've noticed, but it's the formula for any quadrilateral perimeter.
There's also an option that that presents itself with certain special trapezoids - like an isosceles trapezoid, where you need a, b, and c sides. Another example is a right trapezoid, where the length of the bases and one leg are enough to find the shape's perimeter (the last leg is calculated using Pythagoras' Theorem).
Perimeter of a parallelogram formula
In this perimeter calculator you'll find three formulas for the perimeter of a parallelogram:
- The most straightforward one, adding all sides together
Parallelogram Perimeter = a + b + a + b = 2(a + b)
- The perimeter of a parallelogram formula that requires one side and diagonals
Parallelogram Perimeter = 2a² + √(2e² + 2f² - 4a²)
- The perimeter given base, height and any parallelogram angle
Parallelogram Perimeter = 2 * (b + h / sin(α))
Perimeter of a rhombus formula
The perimeter of a rhombus formula is not rocket science, so let's make it concise - it's the same as the perimeter of a square formula!
Rhombus Perimeter = 4a
Another solution to finding the rhombus perimeter requires the diagonal lengths:
Rhombus Perimeter = 2 * √(e² + f²)
Try deriving the formula yourself. You know that the two diagonals of a rhombus are perpendicular to and bisect each other, so you can divide the shape into four congruent right triangles. Each triangle has legs that are e/2 and f/2 long - all you need to do is find the triangle's hypotenuse which is, at the same time, the rhombus side. Then multiply the result by four to find the final perimeter of a rhombus formula.
Perimeter of a kite formula
Formula for the perimeter of a kite is pretty straight forward - just sum up all of the sides:
Kite Perimeter = a + a + b + b = 2(a + b)
Perimeter of an annulus formula
As perimeter is defined as the boundary, an annulus requires us to add the circumference of both concentric circles:
Annulus Perimeter = 2π * R + 2π * r = 2π * (R + r)
Perimeter of a polygon formula (regular pentagon, hexagon, octagon, etc.)
In our perimeter calculator we've also implemented a simple formula for regular polygon perimeter:
Polygon Perimeter = n * a
where n is the number of polygon sides. So, for example, you can calculate the perimeter of a pentagon, hexagon, or octagon.
Additionally, for polygons up to 12 sides, the polygon name will appear in the tool. Awesome!
If you want to determine the perimeter of any polygon, sum the lengths of all its sides:
Polygon Perimeter = Σ aᵢ
where a₁, a₂, ..., aₙ are sides lengths
Σ is the sum symbol (from i = 1 to n)
Or use the vertices coordinates:
Polygon Perimeter = Σ √[(xᵢ₊₁ - xᵢ)² + (yᵢ₊₁ - yᵢ)²]
with x(n+1) = x(1) and y(n+1) = y(1)
