Pentagon Calculator
With this pentagon calculator, you'll find essential properties of a regular pentagon: side, diagonal, height, perimeter, and area, as well as the circumcircle and incircle radius. Type any value, and the remaining parameters will be calculated on the spot.
If you are not sure what a pentagon is or how many sides a pentagon has, keep scrolling, and you'll find clarifying pictures with a short explanation.
What is a pentagon? How many sides does a pentagon have?
Pentagon is a 5-sided polygon. A pentagon can be simple or self-intersecting.
The sum of the internal angles in a simple pentagon is 540°, so every internal angle is equal to 108°. A regular simple pentagon has all five sides equal in length. (In this article, we use the term "regular pentagon" to describe a regular simple pentagon).
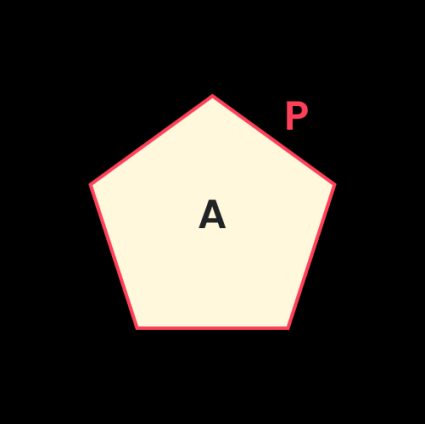
Area and perimeter of a regular pentagon
Area A of a regular pentagon can be calculated from the formula:
area = a² × √(25 + 10√5) / 4, where a is a side of a regular pentagon.
Also, you can find the area having the circumscribed circle radius:
area = 5R² × √[(5 + √5)/2] / 4, where R is the circumcircle radius.
Perimeter P of a regular pentagon is equal to the side length multiplied by the number of vertices. A pentagon is a five-sided polygon, so the perimeter is:
perimeter = 5 × a
How do I find the height and diagonal of a pentagon?
To calculate the height and diagonal of a regular pentagon, all you need to have given is the side length a:
-
diagonal = a × (1 + √5) / 2 -
height = a × √(5 + 2√5) / 2
A pentagon has five diagonals equal in length, which form a pentagram.

How to solve a regular pentagon using this pentagon calculator?

As we now know the pentagon definition, we can have a look at this step-by-step example:
-
Find out what is given. For a regular pentagon, one parameter is enough to find the remaining six.
-
Type the value into the pentagon calculator. Let's take the most famous, almost regular pentagon as an example – the Pentagon building, the headquarters of the US Department of Defense. From the Wikipedia page, we find out that it's 1414 ft wide – it's the height of the pentagram.

The Pentagon, 1,414 feet, 431m (Light blue)
RMS Queen Mary 2, 1,132 feet, 345m (Pink)
US Navy's nuclear-powered USS Enterprise, 1,123 feet, 342m (Yellow)
Airship LZ 129 Hindenburg, 804 feet, 245m (Green)
Imperial Japanese Navy's Yamato, 863 feet, 263m (Dark blue)
Empire State Building, 1,454 feet, 443m (Grey)
Knock Nevis supertanker, 1,503 feet, 458m (Red)
Apple Park main building, 1,522 feet, 458m (Green)
-
The pentagon parameters appear! They are:
- Side – 918.9 ft;
- Diagonal – 1486.8 ft;
- Perimeter – 4594 ft (0.87 mi);
- Area – 33.35 ac;
- Circumcircle radius – 781.6 ft; and
- Incircle radius – 632.4 ft.
Did you notice how enormous it is? Have a look at the perimeter – it's almost a mile! In reality, each side of the building is ~921 feet long – it looks like it's practically a regular pentagon!
Other regular shapes
If you are interested in other regular shapes, have a look at our great tools:
FAQs
How do I calculate the area of a pentagon with side 2?
To compute the area of a regular pentagon from side length, you need to apply the formula:
area = a² × √(25 + 10√5) / 4.
Plugging in a = 2, we obtain area = 2² × √(25 + 10√5) / 4 = √(25 + 10√5) ≈ 6.882.
How do I calculate the apothem of a pentagon?
To compute the apothem of a pentagon with side length a, apply the formula:
apothem = 0.5 × a / tan(π/5)
By simplifying tan, we obtain the following:
apothem = 0.1 × a × √(25 + 10√5 ).
How do I calculate the pentagon internal angle?
To compute the internal angle of a pentagon:
-
Divide
360°by the number of sides:360°/5 = 72°. -
Subtract
72°from180°to get the internal angle of a pentagon:180° - 72° = 108°. -
It follows that the sum of internal angles in a pentagon equals
5 × 108° = 540°.
