Slant Height calculator

Do you want to calculate the slant height of a right circular cone or a right-angled pyramid? If you said "Yes," then our slant height calculator is the right match.

Please read the article below to learn about:

• What is a slant height?
• How to calculate slant height for a right circular cone and a right-angled pyramid?
• How to use our calculator effectively.

The slant height is the side of a right triangle opposite to the right angle. It is also known as the hypotenuse.

For right-angled pyramids, the slant height is the shortest distance measured from the apex to the boundary points located at the base. Particularly, the slant height connects the midpoint of the base to the pyramid's apex.

Some examples of slant height are in the figures below.

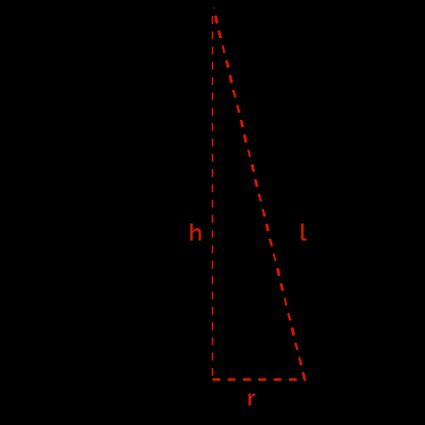
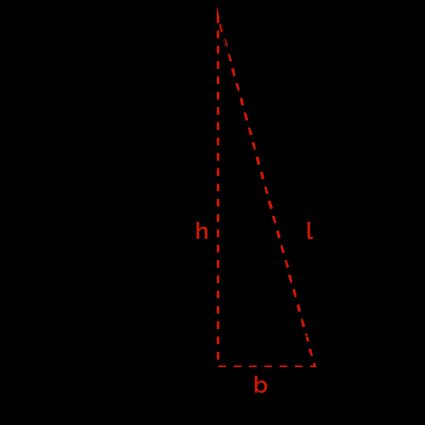
Check out our right square pyramid calc to learn more about the right square pyramid.

Now, let us try to understand how to calculate slant height for different geometric shapes. You can use the following steps to calculate the slant height for different shapes:

1. Find the height $h$ and base length $b$ of the shape for which you want to calculate the slant height $l$.
2. Use the Pythagorean theorem to find the slant height:

• You can apply this procedure to different geometric shapes:

  • Right circular cone – You need height $h$ and base radius $r$ to compute the slant height; and

  • Right angle pyramid – You need height $h$ and base length $b$ to compute the slant height.

The only restriction you need to keep in mind is that the opposite sides of the slant height need to be at $90$ degrees to each other (at right angles).

Cool! Now you know how to calculate the slant height! If you are curious to learn different ways to calculate the slant height of a cone, please check out our slant height of a cone calculator.

Let us consider a hypothetical situation: two persons (P and Q) are in the park. Person $P$ has climbed up the tree, and Person $Q$ is on the ground at a distance of $b$ from the tree. You can find schematics of this problem in the figure below.

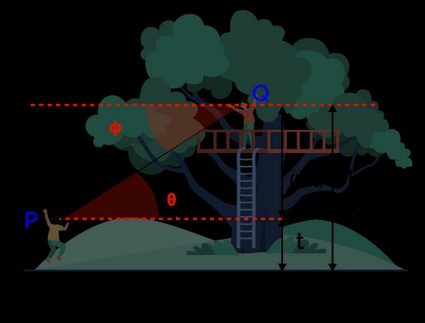
Now the stage is set to solve several problems which involve slant height and other new parameters (you will see them soon 😉).

First problem – We want to calculate how high $h$ Person P is in the tree. To do that, we need to know:

• The distance between the Person P and the tree $b$;
• The angle from the horizontal $\theta$ Person P is looking at the person Q; and
• The distance $t$ between Person P's eye-level and the ground.

1. By using simple trigonometry, we can find out the height $(h-t)$ between Person Q and Person P's eye level:

2. Rearranging the above equation, we can obtain the height Person Q is above the ground:

Angle $\theta$ is called the elevation angle. You notice that Person Q looks down at Person P at the angle $\phi$ from the horizontal, known as the angle of depression. To know about the angle of depression, please check out our angle of depression calculator. In the figure above, the angles of elevation and depression are equal, but this is not always the case.

Second problem – We want to determine the distance between Persons P and Q. You can see from the above figure that we have a right-angle triangle. Therefore, this problem involves slant height $l$. As a result, this problem is essentially a slant height (distance between P and Q) calculation problem.

1. Find at least two out of the following three parameters: $(h-t)$, $b$, and $\theta$.
2. Depending on what is given, you can calculate slant height $l$, or the distance between P and Q, in 3 different cases using the following equations:
   • Given height $(h-t)$ and angle of elevation $\theta$: $l= {(h-t)}/{\sin{\theta}}$
   • Given base $b$ and angle of elevation $\theta$: $l= {b}/{\cos{\theta}}$
   • Given height $(h-t)$ and base $b$: make use of Pythagoras theorem to obtain slant height: $l=\sqrt{(h-t)^2+b^2}$.

To use our calculator effectively, please follow the steps below:

1. Choose the type of shape you want to find the slant height of using the Choose the shape option.
2. Insert the base $b$ or base radius $r$ and height $h$ into the respective fields.
3. Our calculator will give you the slant height $l$ right away.