(Reduced) Row Echelon Form Calculator

Welcome to the reduced row echelon form calculator (or rref calculator for short), where we'll solve a system of equations of your choice using the matrix row reduction and elementary row operations. Also, we give you the option to choose whether you'd like to use the reduced version or not. Based on the choice you make, our tool can be viewed as a Gauss-Jordan elimination calculator (with the first variant) or a Gauss elimination calculator. Moreover, in case your system has an infinite number of solutions, our rref calculator will even tell you what they look like!

Remember all those math scenarios that try to imitate real life? Like a little girl asking you how old she is if, in ten years, her mom will be twice as old as she will be then? You know, just your everyday conversations and everyday problems. Well, equations are what we use to solve them.

Whenever we have some value that we don't know (like the age of the little girl), but we know that it must satisfy some property (like being twice as large as some other number), we describe this connection using equations. We denote the value we don't know with a symbol, which we call a variable. We then write what we know about it with mathematical symbols and operations, such as addition, subtraction, multiplication, or division. The resulting expression is called an equation.

If we have several equations and want all of them to be satisfied by the same number, then what we're dealing with is a system of equations. Usually, they have more than one variable in total, and the most common math problems include the same number of equations as there are variables. For example, suppose that the mother of our little girl tells us that she's three times older than her daughter. Now we know where that wittiness came from)... Anyway, we can translate this new mom statement into an equation as well. Together with the previous one, they would form a system of two equations with two variables: the girl's and the mother's age.

Let's try to see how our reduced row echelon form calculator sees a system of equations. Take this juicy example:

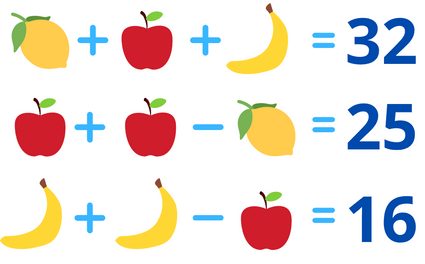
Don't worry, we haven't gone back to kindergarten, we're still working with systems of equations. The above picture may not look like one, but in fact, it is just that. We're so used to seeing variables such as $x$ or $y$ that we tend to forget that it is just a symbol for a value we don't know. And here we have a juicy lemon, a crunchy apple, and a sweet banana, all representing numbers we don't yet know. For simplicity of notation, let's denote them by $x$, $y$, and $z$, respectively. This way we can write an equivalent system of equations:

Now that we look at it, high school killed some of our imagination along the way, hasn't it? Still, we can now easily simplify the system by adding together the same symbols in consecutive equations and write the variables that appear in them in alphabetical order. For example, in the second equation, $y + y - x = 25$, we can add the $y$'s together to obtain $2y - x = 25$ (since we had two copies of $y$). Next, we flip the $x$ variable to the beginning to create an alphabetical order (remember to bring along the number next to it) and get $-x + 2y = 25$. All in all, we obtain

The rref calculator uses the Gauss-Jordan elimination and the Gauss elimination, and both use so-called matrix row reduction. This, in turn, relies on elementary row operations, which are:

1. You can exchange any two equations.
2. You can multiply any equation by a non-zero constant number.
3. You can add a non-zero multiple of any equation to another equation.

What we mean by "you can" is that the system you'd obtain by these operations will be equivalent to the one you started with. This means that the two will have exactly the same solutions.

For example, we could multiply the first equation by, say, $-3$:

and add two copies of the second equation to the third one:

which is

The elementary row operations didn't change the set of solutions to our system. Don't believe us? Go on, type the first and the last system into the reduced row echelon form calculator, and see what you get. We'll wait for you, but expect a "we told you so" when you get back.

We can use the matrix row reduction that we've mentioned in the section above for more practical uses than just having fun with multiplying equations by random numbers. Oh come on, we did have fun, didn't we?

As you might have guessed, it is easier to deal with one variable than with several of them, so why not try to eliminate some of them? Presumably, this (but in German) was the line of thinking of Carl Friedrich Gauss, a mathematician behind the so-called Gauss elimination, but not only: meet him also at the Gauss law calculator. It is an algorithmic procedure that transforms a system of equations into a very easy to deal with form. The idea behind it is (please proceed to read the following instructions in 18th-century German accent):

1. Take an equation with the first variable in it and put that line as the first one in your system.
2. Use elementary row operations on the first equation to eliminate all occurrences of the first variable in all the other equations.
3. Take an equation (different from the first) with the second variable in it and put it as the second one in the system.
4. Use elementary row operations on the second equation to eliminate all occurrences of the second variable in all the later equations.
5. Repeat for subsequent variables until you run out of equations, variables, or self-discipline to finish the exercise.

The system we get in the end is said to be in row echelon form. "So what does the reduced in reduced row echelon form calculator stand for?" How convenient of you to ask! That's where the Gauss-Jordan elimination comes in. It is a slightly improved version of the previous algorithm, first done by Camille Jordan. It took a French mathematician and a few decades to ask the fundamental question: "What if in the end, we divided every line by its first number?" Mind = blown.

In other words, the Gauss-Jordan elimination add-on gives us an additional step in the algorithm:

6. Divide each equation by the coefficient of the first variable occurring in that line.

The system we get with the upgraded version of the algorithm is said to be in reduced row echelon form. The advantage of that approach is that in each line the first variable will have the coefficient $1$ in front of it instead of something complicated, like a $2$, for example. It does, however, speed up calculations, and, as we know, every second is valuable.

It's high time for an example, wouldn't you say?

Recall the system of equations we had in the second section, but the one right before we started playing with elementary row operations:

Before we move on to the step-by-step calculations, let's quickly say a few words about how we can input such a system into our reduced row echelon form calculator. First of all, we have three lines in the system, so we need to tell that to the calculator at the top, in the number of equations field. This will show us a symbolic picture of an arbitrary system of three linear equations.

We need to identify which number corresponds to which symbol from the rref calculator. In the picture, the first equation has symbols $a_1$, $b_1$, $c_1$, and $d_1$, which are respectively next to $x$, to $y$, to $z$, and to the right hand side of the $=$ sign. These are the numbers that we're looking for in our system. Looking at the first of our equations, we identify that $a_1 = 1$, $b_1= 1$, $c_1 = 1$, and $d_1 = 32$ (remember that no number in front of a variable means that the coefficient is equal to $1$).

Similarly, for the next two lines we get $a_2 = -1$, $b_2 = 2$, $c_2 = 0$, $d_2 = 25$, and $a_3 = 0$, $b_3 = -1$, $c_3 = 2$, $d_3 = 16$ (remember that if an equation doesn't have some variable, then the coefficient next to that variable is $0$). If you input all this data into the reduced row echelon form calculator, you'll get a spoiler of what the answer is. Also, note here that our rref calculator doesn't allow non-linear (e.g., quadratic) equations. If you need to solve individual equations of this type, visit the quadratic formula calculator!

We'll now follow the instructions on matrix row reduction given by the Gauss elimination to transform it into a row echelon form. Lastly, we'll do the extra step from the Gauss-Jordan elimination to make it into the reduced version, which is used by default in the rref calculator.

According to the algorithm, we start by choosing an equation with the first variable (in our case, it's $x$) and putting it in the top line. Note, that our system is already in this form, so we don't have to change anything. Next, we use the first equation to eliminate the $x$'s from the other two lines. Observe that we only have to deal with the second one since the third equation has no $x$. To get rid of the $-x$ in the middle line, we need to add to that equation a multiple of the first equation so that the $x$'s will cancel each other out. Since $-x + x = 0$, we need to have $x$ with coefficient $1$ in what we add to the second line. Fortunately, this is exactly what we have in the top equation. Therefore, we add the first line to the second to obtain:

Which is:

Together with the other two equations, this gives:

Great! We now have the two last lines with no $x$'s in them. True, the second equation gained a $z$ that was not there before, but that's just a price we have to pay.

Now we need to do something about the $y$ in the last equation, and we'll use the second line for it. However, it's not going to be as easy as last time - we have $3y$ at our disposal and $-y$ to deal with. Well, the tools they gave us will have to do.

To eliminate $-y$ from the third equation, we'll need to get $y$ (i.e., $y$ with coefficient $1$) from the second one since $-y + y = 0$. To get it from the $3y$, it's enough to divide it by $3$. In other words, in the language of matrix row reduction, we'll add a multiple of $1/3$ (equivalent to dividing by $3$) of the second equation to the bottom line. This gives:

Note how the $1/3$ also appeared on the right side with the $57$. After simplification, this gives:

Which, together with the other two equations, is:

Voilà! That is the row echelon form given by the Gauss elimination. Note, that such systems are obtained in our rref calculator by answering "No" to the question of whether to show the reduced form at the top of the calculator.

To obtain the reduced row echelon form, we follow the sixth step mentioned in the section above - we divide each equation by the coefficient of its first variable. This means that we need to divide the first line by $1$ (the coefficient of $x$), the second by $3$ (the coefficient of $y$), and the third by $7/3$ (the coefficient of $z$). This gives

and marks an end of the Gauss-Jordan elimination algorithm. We can get such systems in our reduced row echelon form calculator by answering "Yes" to the top question (as is done by default).

Observe that now it is easy to find the solution to our system. From the last line, we know that $z = 15$ so we can substitute it in the second equation to get:

From that we get $y = 14$, and we can substitute that and $z = 15$ into the first line to obtain:

Which gives $x = 3$. Coming back to the picture we started with, this means that the lemon is equal to $3$, the apple to $14$, and the banana to $15$. Now that we know our fruits, we can chop them up and have them with some pancakes. We deserve it.