Polygon Calculator
Table of contents
What is a polygon? Polygon definitionHow many sides does a polygon have? Names of polygon shapesRegular polygon formulas: sides, area, perimeter, anglesHow to use this polygon calculator — an exampleWith this polygon calculator, you can find the essential properties of any n-sided regular polygon. Whether you are looking for the area of a heptagon or the angles in a decagon, you're at the right place. Below, you'll find the polygon definition and a table with the names of polygons along with their shapes. After reading this short article, you'll know what a polygon is and how many sides a particular polygon has — keep reading, or simply give this calculator a go!
What is a polygon? Polygon definition
A polygon is a 2D closed figure made up of straight line segments. That's the polygon definition. But what does it look like? Many shapes you learned about are polygons - triangles, squares, parallelograms, rhombus, kites, pentagons, hexagons, octagons... A lot of them. But popular shapes that are not polygons also exist - take a circle and an ellipsis as an example.
Polygons are classified based on their sides and angles, as well as their convexity, symmetry, and other properties.
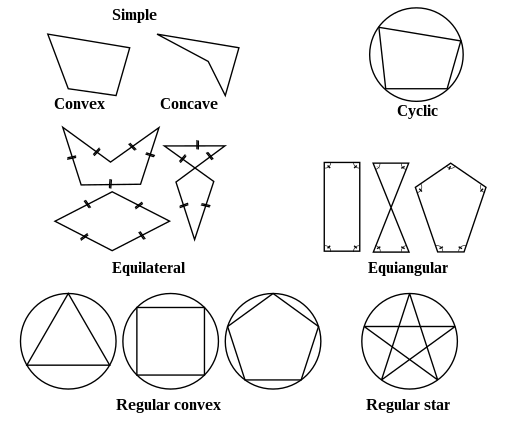
In this polygon calculator, we solve the properties of regular polygons - the special polygon types which are:
- Equiangular — all angles are equal in measure
- Equilateral — all sides have the same length
Every regular polygon with n sides is formed by n isosceles triangles.
How many sides does a polygon have? Names of polygon shapes
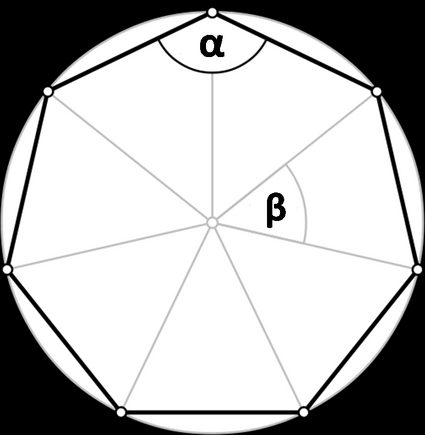
The answer to the question depends on which polygon you have on your mind. "Usually, you can use the polygon name as a hint to deduce how many sides it has - the prefixes come from Greek numbers.
Polygon | Name | n (sides) | Regular polygon shape | α | β |
|---|---|---|---|---|---|
3 - sided polygon | trigon (equilateral triangle) | 3 |  | π/3 = 60° | 2π/3 = 120° |
4 - sided polygon | tetragon, quadrilateral (square) | 4 |  | π/2 = 90° | π/2 = 90° |
5 - sided polygon | pentagon | 5 |  | 3π/5 = 108° | 2π/5 = 72° |
6 - sided polygon | hexagon | 6 |  | 2π/3 = 120° | π/3 = 60° |
7 - sided polygon | heptagon (septagon) | 7 |  | 5π/7 = 128.57° | 2π/7 = 51.43° |
8 - sided polygon | octagon | 8 |  | 3π/4 = 135° | π/4 = 45° |
9 - sided polygon | nonagon | 9 | | 7π/9 = 140° | 2π/9 = 40° |
10 - sided polygon | decagon | 10 |  | 8π/10 = 144° | π/5 = 36° |
n - sided polygon | n - gon | n |  | (n-2) × 180°/n | 360°/n |
If your polygon has 11 or more sides, it's easier to write 11-gon, 14-gon, 20-gon ... "100-gon", etc. But if you're really curious...
Polygon | Name | n (sides) | α | β |
|---|---|---|---|---|
11 - sided polygon | Hendecagon (undecagon) | 11 | 147.273° | 32.73° |
12 - sided polygon | Dodecagon | 12 | 150° | 30° |
13 - sided polygon | Triskaidecagon | 13 | 152.308° | 27.69° |
14 - sided polygon | Tetrakaidecagon | 14 | 154.286° | 25.71° |
15 - sided polygon | Pentadecagon | 15 | 156° | 24° |
16 - sided polygon | Hexakaidecagon | 16 | 157.5° | 22.5° |
17 - sided polygon | Heptadecagon | 17 | 158.824° | 21.18° |
18 - sided polygon | Octakaidecagon | 18 | 160° | 20° |
19 - sided polygon | Enneadecagon | 19 | 161.053° | 18.98° |
20 - sided polygon | Icosagon | 20 | 162° | 18° |
30 - sided polygon | Triacontagon | 30 | 168° | 12° |
40 - sided polygon | Tetracontagon | 40 | 171° | 9° |
50 - sided polygon | Pentacontagon | 50 | 172.8° | 7.2° |
60 - sided polygon | Hexacontagon | 60 | 174° | 6° |
70 - sided polygon | Heptacontagon | 70 | 174.857° | 5.14° |
80 - sided polygon | Octacontagon | 80 | 175.5° | 4.5° |
90 - sided polygon | Enneacontagon | 90 | 176° | 4° |
100 - sided polygon | Hectagon | 100 | 176.4° | 3.6° |
1,000 - sided polygon | Chiliagon | 1,000 | 179.64° | 0.36° |
10,000 - sided polygon | Myriagon | 10,000 | 179.964° | 0.036° |
1,000,000 - sided polygon | Megagon | 1,000,000 | ~180° | ~0° |
10100 - sided polygon | Googolgon | 10100 | ~180° | ~0° |
Regular polygon formulas: sides, area, perimeter, angles
If you want to calculate the regular polygon parameters directly from equations, all you need to know is the polygon shape and its side length:
1. Area
area = n × a² × cot(π/n)/ 4
Where n- number of sides, a - side length
Other equations, which use parameters such as the circumradius or perimeter, can also be used to determine the area. You can find them in a dedicated calculator of polygon area.
2. Perimeter
perimeter = n × a
Read more about polygon perimeter in the perimeter of a polygon calculator.
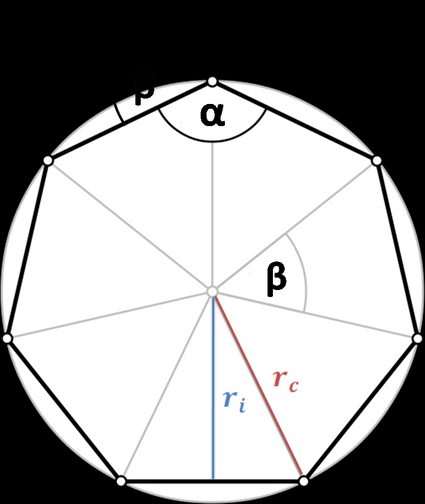
3. Angles :
α = (n - 2) × π / n, whereαis an interior angle;β = 2 × π / n, whereβis an exterior angle.
If you're particularly interested in angles, you may want to take a look at our polygon angle calculator.
4. Incircle radius (apothem)
ri = a / (2 × tan(π/n))
5. Circumcircle radius
rc = a / (2 × sin(π/n))
All these equations are implemented in our polygon calculator.
How to use this polygon calculator — an example
If you're still wondering how to use our tool, have a look at the following example:
- Choose the polygon shape and type its number of sides. To calculate the properties of, e.g., a nonagon, type 9 into the number of sides box.
- Enter one parameter. One given value is enough. Assume that we know the perimeter of our shape; let's say it's 18 in.
- Great! Our polygon calculator finds all the remaining values! We determined that:
- side = 2 in
- area = 24.727 in²
- α = 140°
- β = 40°
- rc = 2.924 in
- ri = 2.7475 in