Radical Calculator

If you want to find the radical numbers of any $n^{\text{th}}$ degree radical, then this radical calculator is just for you. The tool to your left is straightforward to use, as it only needs two values to estimate the third one. It can also do the reverse calculations!

If you are wondering what radical form is and want to learn about the radical notation, read the following article for all the basic information about this math operation. Below you'll also find the radical definition and some examples explaining the problem of adding and subtracting radicals. There's also answers to the questions "How to multiply radicals?" and "How to divide radicals?". It might not be as easy as you think! 😮

If you came here for the simplest root, the one with a degree of 2, then check out our square root calculator to find a more comprehensive description of square roots.

In general, the radical function is a root of a number $x$ for which we use the radical symbol $\sqrt[n]{}$, with the superscript $n$ describing the degree of the root. The radical definition is:

$r^n = x$,

and therefore:

$r = x^{\frac{1}{n}}$,

where $r$ is the result of the radical. So, in other words, radicalization is the opposite operation to exponentiation, for which the exponent is a fraction. To make writing the radicals easier, we use the radical notation:

$r = \sqrt[n]{x}$,

which means the same thing as the above equation.

It turns out that you cannot calculate the root of any number. What are the conditions for radical numbers then?

In general, the number you want to root should be positive, although it is possible to find the answer when the degree is odd, e.g., when $n = 3$ ($\sqrt[3]{x}$ – cube root), as $\sqrt[3]{8}$ = 2 and -2.

Secondly, the degree of the radical is usually a positive integer number. Technically, you can use fractions, but in that case, exponentiation is a better way to present the computation.

To conclude the radical notation, for the radical $\sqrt[n]{x}$:

• $n$ – should be a positive integer; and
• $x$ – should be any positive number.

The radical calculator consists of three fields that should be self-explanatory. Fill in any two boxes and we will estimate the third one automatically:

• Number – that's the number for which you'd like to find the radical. We decided not to allow entering negative values here even if the radical degree is odd. That's because, in most cases, you would obtain multiple answers (like in the quadratic formula), including complex numbers, which we wanted to avoid in this calculator. If you insist on negative numbers, then check our root calculator (a very similar tool to this radical calculator, but which allows negative numbers) or complex root calculator dedicated to finding radicals of any number.

• Radical degree (n) – as we mentioned before, $n$ should be a positive integer. However, since you can treat a radical function as an exponent, technically, it's possible to calculate the radical for other degrees. You can input non-integer values as well as negative numbers if you want so.

• Radical (nᵗʰ radical) – the $n^{\text{th}}$ radical is probably the reason you came here. We display a more advanced result under this field, i.e., with step-by-step radical simplification (if possible). For example, try to find $\sqrt[4]{162}$ and see what happens. As a bonus, we've enabled you to input a negative number into the last field. Why is it possible? Because all that we said about multiple answers and complex numbers before, doesn't apply here. Doing all the math the other way around, i.e., estimating an exponent, is a well-defined operation 🎉

The radical calculator might be a convenient tool that you can use to estimate the radicals of any degree, find perfect radicals (by inputting numbers in the third field), or just to verify your answer that you worked on paper (or in your head if you're some kind of math wizz). Speaking of calculating things by hand... we haven't finished yet! Below, we've prepared some sections about adding and subtracting radicals, how to multiply radicals, and how to divide radicals. All of them consist of enlightening examples. So, hesitate no more and dive in the sea of the rules for radicals!

Do you want to find out how to add radicals, or what are the rules for subtracting radicals? It isn't as simple as adding two numbers. For example, this is WRONG:

❌ $\sqrt[4]{7} + \sqrt[3]{4} = \sqrt[7]{11}$ ❌

What is the procedure of adding radicals, then? You can do it only if the degree and the number under the radical sign are the same:

✅ $\sqrt[4]{7} + 2\sqrt[4]{7} = 3\sqrt[4]{7}$ ✅

✅ $5\sqrt[3]{5} + 3\sqrt[3]{5} = 8\sqrt[3]{5}$ ✅

There are no exceptions to that! However, in some cases, you can manipulate the number under the radical symbol by bringing out a number that can be rooted. For example, can you add $\sqrt[3]{192}$ and $\sqrt[3]{3}$? It might seem impossible, but if you make some simplification of $\sqrt[3]{192}$:

$\sqrt[3]{192} = \sqrt[3]{64 \times 3} = \sqrt[3]{64} \times \sqrt[3]{3} = 3\sqrt[3]{3}$,

you realize that both requirements of the adding radicals are fulfilled!

$\sqrt[3]{192} + \sqrt[3]{3} = 3\sqrt[3]{3} + \sqrt[3]{3} = 4\sqrt[3]{3}$

You can always use our radical calculator to check whether your radical numbers can be simplified or not. Are you fighting with a similar problem but with fractions? Check out our dedicated tool: the simplify fraction calculator!

What about subtracting radicals? There is not much difference 😎 You still need to have the same radical degree and number under the radical sign:

$5\sqrt[6]{9} - 2\sqrt[6]{9} = 3\sqrt[6]{9}$

Thankfully, this is much easier than adding and subtracting radicals. However, there are some additional rules for when you want to multiply two radicals. Namely speaking, the degree of both radicals must be the same. If this is true, then you can multiply the numbers below the radical symbol, for example:

$\sqrt[4]{7} \times \sqrt[4]{4} = \sqrt[4]{7 \times 4} = \sqrt[4]{28}$

What if your radical form also consists of a number before the radical itself? Even in this case, it is still simpler than adding radicals because you don't care much and simply multiply numbers before radicals:

$4\sqrt[3]{3} \times 2\sqrt[3]{5} = (4 \times 2)\sqrt[3]{3 \times 5} = 8\sqrt[3]{15}$

$5\sqrt[3]{2} \times \sqrt[3]{12} = (5 \times 1)\sqrt[3]{2 \times 12} = 5\sqrt[3]{24} = 10\sqrt[3]{3}$

In the last example, we simplified the radical $\sqrt[3]{24}$, just like we did when we learned How to add radicals in the previous section. In this case:

$\sqrt[3]{24} = \sqrt[3]{8 \times 3} = \sqrt[3]{8} \times \sqrt[3]{3} = 2\sqrt[3]{3}$

In the Radical definition math – what does radical mean? section, we explained the radical meaning – it's the reverse operation to exponentiation. Therefore, rules for radicals and exponentiation are similar. You can use this knowledge to multiply radicals of different degrees but with the same number under the radical symbol. Take a look at this example:

$\sqrt[4]{2} \times \sqrt[3]{2} =$

We know what radical form (the alternative one, with fractions) is:

$2^{\frac{1}{4}} \times 2^{\frac{1}{3}} =$

you can perform a multiplication of the exponents (i.e., add fractions):

$2^{\frac{1}{4} + \frac{1}{3}} = 2^{\frac{7}{12}} =$

Eventually, you can go back to the original radical form:

$\sqrt[12]{2^7} = \sqrt[12]{128}$

Isn't that a simpler radical form? 😀

After learning how to add radicals, subtract them, and multiply them, the remaining basic arithmetic operation left is dividing radicals. Basically, the rules for dividing radicals are the same as for multiplication, i.e., if two radicals have the same degree, you can simply divide the numbers under the radical symbol, for example:

$\sqrt[5]{8} / \sqrt[5]{4} = \sqrt[5]{8 / 4} = \sqrt[5]{2}$

or

$5\sqrt[3]{15} / 2\sqrt[3]{5} = (5 / 2)\sqrt[3]{15 / 5} = 2.5\sqrt[3]{3}$

Again, if you want to divide radicals of different degrees but the same numbers under the radical sign, use the formula from the Radical definition math – what does radical mean? section. As always, here's an example to picture this approach:

$\sqrt[4]{6} / \sqrt[5]{6}$

$= 6^{\frac{1}{4}} / 6^{\frac{1}{5}}$

Be careful, though! This time you need to subtract fractions:

$6^{\frac{1}{4} - \frac{1}{5}} = 6^{\frac{1}{20}}$

The final answer is:

$= \sqrt[20]{6}$

The simplest radical function has the following form:

$f(x) = \sqrt[n]{x}$,

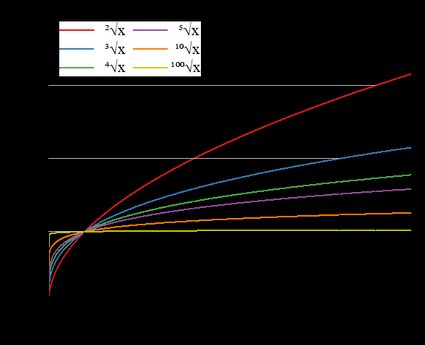
where $n$, a radical degree, is usually a positive integer. In particular, for $n = 2$, we obtain a simple square root $\sqrt{x}$ (in this special case, you shouldn't write $2$ above the radical symbol). The radical graph looks just like half a parabola rotated by 90 degrees. As you can see in the picture below, for greater degrees of $n$, the radical graph has an increasingly flat shape.

We can further generalize the radical function, if needed, by adding three extra parameters:

$f(x) = a \times \sqrt[n]{b\times x - h} + k$,

where:

• $a$ scales the radical graph on the y-axis;
• $b$ scales the radical graph on the x-axis;
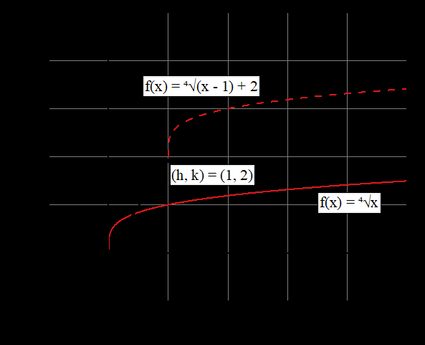
• $h$ offsets the radical function on the x-axis; and
• $k$ offsets the radical function on the y-axis.

Does that sound complicated? 🤓 In the figure below, we explained how the parameters $h$ and $k$ influence the radical function. You can see that it's translated by a vector $(h, k)$.