Perimeter of a Quadrilateral Calculator

Q: What is a quadrilateral?

A quadrilateral is a closed shape with four straight sides, angles, and vertices. Some examples of quadrilaterals are square, kite, rhombus, trapezoid, and parallelogram. Read more

Q: What is a concave quadrilateral?

A concave quadrilateral is a four-sided figure with one interior angle measuring more than 180 degrees. Additionally, a concave quadrilateral has one diagonal that lies in the area of the actual form. Read more

Q: How do I calculate the perimeter of a quadrilateral given its coordinates?

To calculate the perimeter of a quadrilateral when given its coordinates, you need to follow these steps: Get the coordinates of each side. Put the coordinates of each side into the distance formula and calculate the lengths . Find the total length of all the sides. The answer from step 3 is your perimeter . Read more

Created by Adena Benn

Reviewed by Steven Wooding

Last updated: Jan 18, 2024

Table of contents:

Do you need a perimeter of a quadrilateral calculator to help you solve those math problems? Do you know the coordinates of a shape with four sides but have no idea 😕 how to calculate the perimeter and need some help❓ We have just the tool you need. Our how to find the perimeter of a quadrilateral calculator is designed to help you find the perimeter of any shape with four sides and four vertices.

In this article, you will learn more about:

What a quadrilateral is;
What is a concave quadrilateral;
How to find the perimeter of a quadrilateral given four sides;
How to calculate the perimeter of a quadrilateral using the coordinates; and
How to use our perimeter of a quadrilateral calculator.

So what is the perimeter of a quadrilateral?

The perimeter of a quadrilateral is the distance around the quadrilateral. So to find the perimeter of a quadrilateral 🟧, we need to add up all the sides. The real difficulty, however, is that we do not always know what those measurements are in mathematics or real life. This is where our calculator comes in.

🔎 If you have a rectangle, you can find its perimeter with our perimeter of a rectangle calculator.

Keep reading to learn how to find the perimeter of quadrilaterals when all the sides are known as well as when only the coordinates of the vertices are known.

What is a quadrilateral?

A quadrilateral is a closed shape with four straight sides, angles, and vertices. Some examples of quadrilaterals are square, kite, rhombus, trapezoid, and parallelogram.

What is a concave quadrilateral?

A concave quadrilateral is a four-sided figure with one interior angle measuring more than 180 degrees. Additionally, a concave quadrilateral has one diagonal that lies in the area of the actual form.

How to find the perimeter of a quadrilateral given its sides

Finding a quadrilateral's perimeter when the sides are known is a pretty simple task. We add all the sides together. Of course, sometimes, we may only know two sides. With most quadrilaterals, this is still pretty simple.

For instance, if the quadrilateral is a square, rectangle, parallelogram, or any shape with two equal opposite sides and angles, the usual solution is to multiply the length by two and the width by two, then add the answers together to arrive at the perimeter.

However, we cannot do this for more irregular shapes like a trapezoid unless we have more information.

How to find the perimeter of a quadrilateral when given the coordinates

To find the perimeter of a quadrilateral, when you know the coordinates of the vertices, you:

Use the distance formula to find the length of each side.

\small \qquad D = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}

Put in the matching $x$ and $y$ coordinates of all the sides and calculate the lengths.
Once you complete step 2, you need to add all the answers together.
The result is the perimeter.

Example:

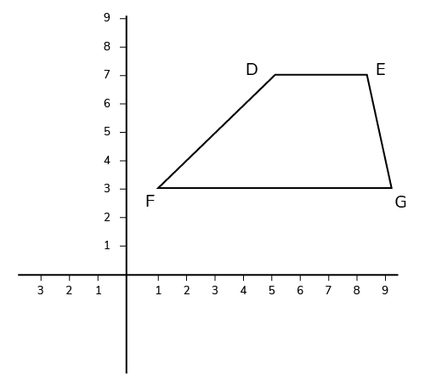
Given the coordinates of quadrilateral DEFG as (5, 7), (8, 7), (1, 3), and (9, 3) respectively, find the perimeter.

Let the values of D, (5 and 7) be x₁, y₁ the values of E, (8, 7), are x₂, y₂ the values F, (1, 3) are x₃, y₃ and the values of G, (9, 3) are x₄, y₄.

Now plot the graph so you can clearly see which points connect to form your quadrilateral.

Using the distance formula, let us find line DE:

\small \begin{align*} DE &= \sqrt{(8 - 5)^2 + (7 - 7)^2}\\[.5em] &= \sqrt{(3)^2 + (0)^2}\\[.5em] &= \sqrt{(3)^2 }\\[.5em] &= 3 \end{align*}

Now let's find line FG:

\small \begin{align*} FG &= \sqrt{(9 - 1)^2 + (3 - 3)^2}\\[.5em] &= \sqrt{(8)^2}\\[.5em] &= \sqrt{64}\\[.5em] &= 8 \end{align*}

Now, let's find the length of line EG:

\small \begin{align*} EG &= \sqrt{(8 - 9)^2 + (7 - 3)^2}\\[.5em] &= \sqrt{(-1)^2 + (4)^2}\\[.5em] &= \sqrt{1 + 16}\\[.5em] &= \sqrt{17}\\[.5em] &= 4.1 \end{align*}

Finally, let us calculate the last side:

\small \begin{align*} FD &= \sqrt{(5 - 1)^2 + (7 - 3)^2}\\[.5em] &= \sqrt{(4)^2 + (4)^2}\\[.5em] &= \sqrt{16 + 16}\\[.5em] &= \sqrt{32}\\[.5em] &= 5.7 \end{align*}

Once you have found the lengths of all the sides, the only thing left to do is add all the lengths together. So the perimeter of the quadrilateral is:

\small \begin{align*} DEFG &= 3 + 8 + 4.1+ 5.7\\[.5em] &= 20.8 \end{align*}

How to use our perimeter of a quadrilateral calculator

The perimeter of a quadrilateral calculator is two calculators in one. It allows us to calculate the distance around any four-sided shape using either the known length of all sides or the coordinates of all the vertices. So here are the steps you should follow to use our calculator:

To select which of these calculators you wish to use, choose from the options available in the field labeled Given.
If you choose the option 4 sides, you should now enter the values of the four sides.
Once you have completed step 2, the calculator will show your answer in the field labeled perimeter.
If you choose four vertices in the Given field, you will see a second calculator where you will need to fill in the x and y coordinates of the shape whose perimeter you wish to calculate.
Once you have filled in the coordinates, our calculator will return both the length of each side as well as the perimeter of the shape.

Other quadrilateral calculators

Here are some similar calculators that may interest you:

FAQ

How do I calculate the perimeter of a quadrilateral given its coordinates?

To calculate the perimeter of a quadrilateral when given its coordinates, you need to follow these steps:

Get the coordinates of each side.
Put the coordinates of each side into the distance formula and calculate the lengths.
Find the total length of all the sides.
The answer from step 3 is your perimeter.

Adena Benn

Given

Side (a)

Side (b)

Side (c)

Side (d)

Perimeter

AreaArea of a rectangleArea of crescent… 20 more