Area of Quadrilateral Calculator

Our area of quadrilateral calculator will help you to determine the area of any quadrilateral with different known parameters. This article will briefly discuss quadrilaterals and the different quadrilateral area formulae available. So join us below to learn how to find the area of a quadrilateral.

Q: How do you define a quadrilateral?
A: "Four points joined by straight lines."

Q: But what if the points are collinear?
A: "The points have to be non-collinear."

Q: But what if the lines don't form a closed figure?
A: A quadrilateral is a closed figure (a polygon) with four sides.

You can see quadrilaterals everywhere, from swimming pools and soccer fields to buildings and bridges. Recognizing the geometry of a structure will greatly simplify calculations. There are many types of quadrilaterals, such as rectangles and trapezoids. To estimate the latter's area quickly, you can head to Omni's trapezoid calculator. Let's first learn how to calculate the area of an irregular quadrilateral.

There are various methods to calculate the area of an irregular quadrilateral based on which parameters are known:

1. From four sides and two opposite angles:

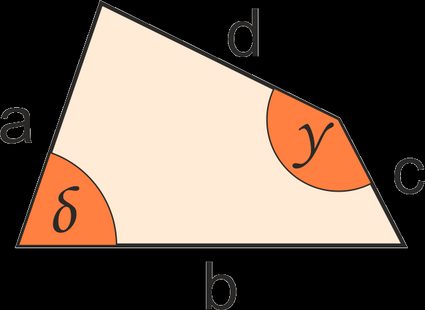
A = √((s - a)(s - b)(s - c)(s - d) - a · b · c · d · cos²(δ · γ))

where:

• A — Area of the quadrilateral;
• s — The semi-perimeter of the quadrilateral, equal to 0.5 · (a + b + c + d);
• a, b, c, d — The four sides of the quadrilateral; and
• δ, γ — Any two opposite angles of the quadrilateral.

2. From its diagonals and the angle between them:

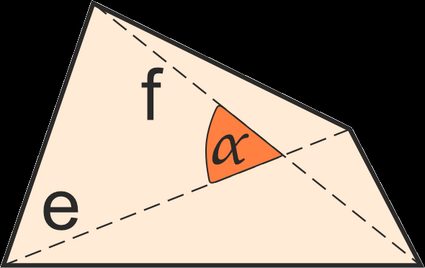
A = 0.5 · e · f · sin(α)

where:

• e, f — The lengths of the two diagonals of the quadrilateral; and
• α — The angle between the two diagonals. There are two unique angles between the two diagonals, α and (π-α). Since sin(π-α) = sin(α), the quadrilateral area formula yields the same result for both angles.

3. From the bimedians and the angle between:

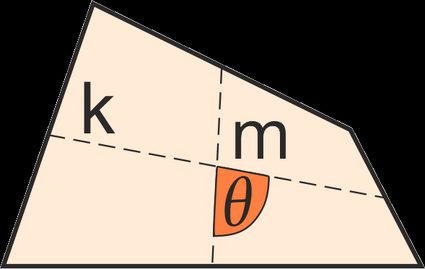
A = m · k · sin(θ)

where:

• m, k — The lengths of the two bimedians of the quadrilateral; and
• θ — The angle between the two bimedians. Again, since sin(π-θ) = sin(θ), we can use this formula to calculate quadrilateral area irrespective of our choice of angle.

4. From the Cartesian coordinates of the quadrilateral's vertices:

A = 0.5 · (x₁y₂ - y₁x₂ + x₂y₃ - y₂x₃ + x₃y₄ - y₃x₄ + x₄y₁ - y₄x₁)

where (x₁, y₁), (x₂, y₂), (x₃, y₃), (x₄, y₄) are the coordinates of the four vertices of the quadrilateral.

We've seen how to find the area of a quadrilateral with an irregular shape. For quadrilaterals like squares and rectangles, other simpler formulae for area exist:

1. Rectangles: A quadrilateral whose opposite sides are equal in length, and all angles are right angles.

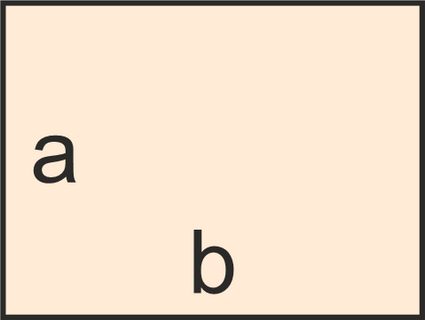
Its area is given by:

A = b · a

where:

• b — The rectangle's length; and
• a — The rectangle's breadth.

2. Square: A quadrilateral with all sides equal in length, and all its angles are right angles.

Its area is given by:

A = a²

where a is the square's side length.

3. Parallelogram: A quadrilateral whose opposite sides are equal in length and parallel to each other, and the opposite angles are equal.

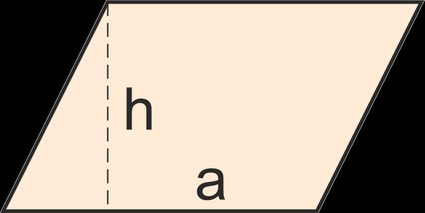
The formula for a parallelogram's area is:

A = b · h

where:

• b — The parallelogram's base; and
• h — The parallelogram's height (the perpendicular distance between the base and its opposite side).

4. Rhombus: A quadrilateral whose four sides are equal in length.

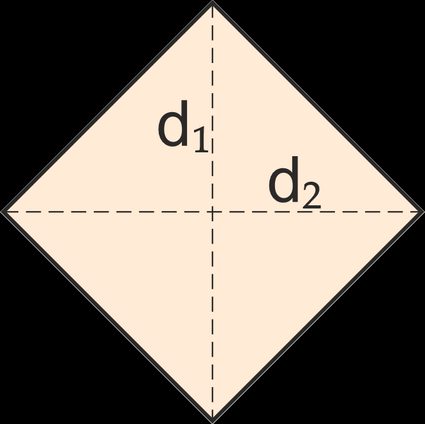
Its area is given by:

A = 0.5 · d₁ · d₂

where d₁, d₂ are the rhombus's diagonals.

5. Trapezoid: A Trapezoid (or trapezium) is a quadrilateral with at least one pair of parallel sides.

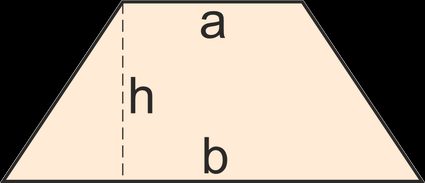
The area of a trapezoid is:

A = 0.5 · h · (a + b)

where:

• a, b — The lengths of the parallel sides of a trapezoid; and
• h — The trapezoid's height.

6. Kite: A kite is a quadrilateral in which two pairs of adjacent sides are equal in length.

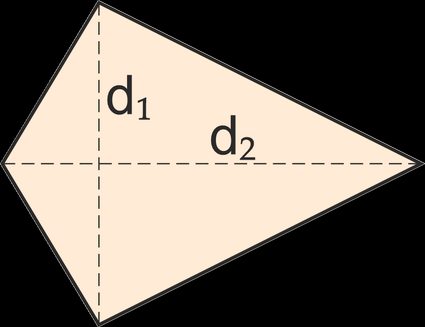
Its area is given by:

A = 0.5 · d₁ · d₂

where d₁, d₂ are the kite's diagonals.

Our area of quadrilateral calculator is a powerful tool capable of calculating the area of any quadrilateral from different known parameters:

• Select the type of the quadrilateral. Choose unknown for irregular quadrilaterals.
• For irregular quadrilaterals, you can choose which parameters are given.
• Enter the parameters in their respective fields with proper units.
• This area of a quadrilateral calculator will instantly calculate the answer for you.

Here are some other quadrilateral calculators for you to explore:

• Quadrilateral; and
• Perimeter of a quadrilateral.

25 cm². To calculate this, follow these steps:

1. Multiply the square's side by itself to get A = 5 × 5 = 25.
2. Verify your result with our area of a quadrilateral calculator.

The sum of all the angles in a quadrilateral is 360° or 2π radians. Think of a quadrilateral as a fusion of two triangles that share a common side (the diagonal).