Percentage Calculator

This percentage calculator is a tool that lets you do a simple calculation: what percent of X is Y? The tool is pretty straightforward. All you need to do is fill in two fields, and the third one will be calculated for you automatically. This method will allow you to answer the question of how to find a percentage of two numbers.

Furthermore, our percentage calculator also allows you to perform calculations in the opposite way, i.e., how to find a percentage of a number. Try entering various values into the different fields and see how quick and easy-to-use this handy tool is. Is only knowing how to get a percentage of a number is not enough for you?

Other than being helpful with learning percentages and fractions, this tool is useful in many different situations. You can find percentages in almost every aspect of your life! Anyone who has ever been to the shopping mall has surely seen dozens of signs with a large percentage symbol saying "discount!". And this is only one of many other examples of percentages. They frequently appear, e.g., in finance, where we use them to find an amount of income tax or sales tax, or in health to express what is your body fat.

Keep reading if you would like to see how to find a percentage of something, what the percentage formula is, and the applications of percentages in other areas of life, like statistics or physics.

Our percentage calculator has four sections. The following instructions should help you select the right section and put it to good use:

1. The section What is p% of x? will calculate the given percentage of a number:

   1. Enter the percentage.
   2. Enter the number of which you need to find the percentage.
   3. The percent number appears at once.

For example, say you scored 80% on a test. If the test was for 30 marks, your score is 24 marks.

You can even calculate in reverse. This would allow you to, for instance, calculate your percentage based on your score. In a test for 30 marks, if you scored 27 marks, your percentage is 90%.

2. The section x is what percent of y? will determine the percentage of two given numbers:

   1. Enter the number whose percentage you want to determine.

   2. Provide the number against which this percentage must be evaluated.

   3. The calculator gives you the percentage instantly.

For instance, say Gavin's rent is $1245 per month, while his monthly budget is $4000. When we enter 1245 in the first field and 4000 in the second, we can determine that his house rent takes up 31.125% of his monthly budget.

This section also works in reverse. Say Gavin wants to move to a place that costs no more than 25% of his monthly budget. When we input 25% as the percentage and 4000 in the second field, the calculator informs us that $1000 is the maximum rent Gavin can afford.

3. The section x is p% of what? is useful to find the value for which a given number comprises a known percentage:

   1. Enter the number for which you know the percentage.

   2. Provide the percentage.

   3. The calculator will give you the number you seek right away.

Let us see this with an example — 10 is 5% of which number? Enter 10 in the first field and 5% as the percentage. You can immediately see that the result is 200.

You can even use this in reverse. Entering 25% percentage and 50 in the third field, we learn that 12.5 is 25% of 50.

4. The section What is x increased/decreased by p%? will help you determine the effects of an increase or decrease in a value by a given percent:

   1. Enter the initial value.

   2. Select whether the change is an increase or decrease.

   3. Enter the percent by which the initial value changes.

   4. The changed value is displayed to you instantly.

For example, say that the price of a candy bar increased by 30%. Enter the original price, $5, in the first field. Next, choose that the change is an increase. Finally, enter 30% percent, and we learn the new price is $6.50.

It also works in reverse. Say we know the discounted price of an item is $44. If the discount is 10%, our calculator will tell us the original price is $48.89.

There is a lot of fascinating information about percentages in the following section, starting with what percentages are and how to find them. So grab some snacks and browse through it.

Percentage is one of many ways to express a dimensionless relation between two numbers (the other methods being ratios and fractions). Percentages are very popular since they can describe situations that involve large numbers (e.g., estimating chances for winning the lottery), averages (e.g., determining the final grade of your course), as well as very small ones (like the volumetric proportion of NO₂ in the air, also frequently expressed by PPM — parts per million).

One percent is a hundredth. As a percent sign, we usually use %, but sometimes it is denoted by pct. It means that 5 percent is the same as 5%, 5 pct, 0.05, 5/100, or five-hundredths. It is as simple as that, and this percentage calculator is a tool dedicated to working with decimal fractions and percentages. If you're seeking more complicated problems, try to figure out how to calculate the percentage of a percentage.

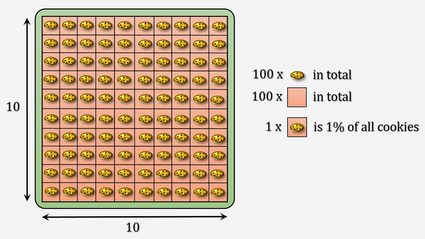
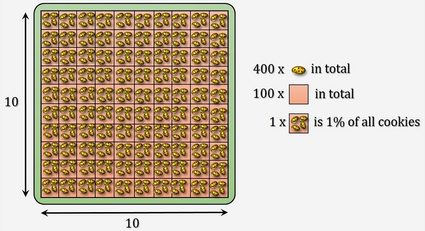
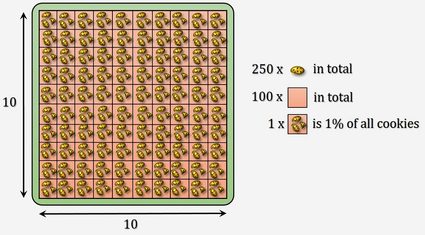
This is all nice, but we usually do not use percentages just by themselves. Mostly, we want to answer how big is one number in relation to another number?. To try to visualize it, imagine that we have something everyone likes, for example, a large packet of cookies (or donuts or chocolates, whatever you prefer 😉 — we will stick to cookies). Let's try to find an answer to the question of what is 40% of 20? It is 40 hundredths of 20, so if we divided 20 cookies into 100 even parts (good luck with that!), 40 of those parts would be 40% of 20 cookies. Let's do the math: 40/100 × 20 = 8. A handy little tip: to divide by 100, simply move the dot two spaces to the left. In our calculation, 40/100 × 20 could be done as (40 × 20)/100 (it's the same thing). 40 × 20 is 800. By moving the dot in 800 by two digits to the left, you get 8.00, and when you get rid of all unnecessary zeros, you obtain 8. In our calculator, enter 40 and 20 (so it reads "40% of 20" is 8).

A percentage is also a way to express the relation between two numbers as a fraction of 100. In other words, the percentage tells us how one number relates to another. If we know that number A is 25% of number B, we know that A to B is like 25 is to 100, or, after one more transformation, like 1 to 4, i.e., A is four times smaller than B. This is what the percentage calculator teaches; what is a percentage and how to find a percentage of two numbers.

How to find a percentage of something? It's easiest to explain what is the percentage with cookies. It is surprising how often cookies save the day, right? Say we have a big drawer with 100 compartments (a 10 × 10 grid). Every compartment is one hundredth or 1% of the whole drawer. We then fill this drawer with cookies in a way that gives us exactly the same number of cookies in each compartment.

At first, let's start with the most straightforward example with 100 cookies. How to get the percentage of several, let's say, five cookies? It's easy: every compartment gets exactly one cookie. So one percent of 100 is one cookie, and five percent is five cookies.

Let's go with something a bit harder and four times more delicious: 400 cookies! We're dividing them evenly, and every compartment gets four cookies. Cookies look smaller, but in our imagination, they are the same, just the drawer is much bigger! One percent of 400 is 4. How about 15 percent? It's 15 compartments times four cookies — 60 cookies. Our tummies start to ache a little, but it has never stopped us from eating more cookies!

Now, something even harder — 250 cookies. Oh-oh, we divided up the first 200 cookies, placing two in every compartment. Now we are left with 50 cookies that need to be spread evenly, hmmm, it's half a cookie in every box. How to calculate the percentage? You are right — this time, 1 percent of the total number of 250 cookies is 2.5. How many do we have in 15 boxes? 2.5 × 15 is 37.5.

So what is percentage good for? As we wrote earlier, a percentage is a way to express a ratio. Say you are taking a graded exam. If we told you that you got 123 points, it really would not tell you anything. 123 out of what? Now, if we told you that you got 82%, this figure is more understandable information. Even if we told you, you got 123 out of 150; it's harder to feel how well you did. A week earlier, there was another exam, and you scored 195 of 250, or 78%. While it's hard to compare 128 of 150 to 195 of 250, it's easy to tell that an 82% score is better than 78%. Isn't the percent sign helpful? After all, it's the percentage that counts!

What about decimal fractions and percentages? Percentages can easily be converted to decimals. Just divide the percentage by 100, and you are set. 15% is the same as 0.15. So as we have shown before, 0.15 of 250 cookies is thirty-seven and a half.

Percentages are sometimes better at expressing various quantities than decimal fractions in chemistry or physics. For example, it is much more convenient to say that the percentage concentration of a specific substance is 15.7% than that there are 18.66 grams of substance in 118.66 grams of solution. Another example is efficiency (or its special case — Carnot efficiency). Is it better to say that a car engine works with an efficiency of 20% or that it produces an energy output of 0.2 kWh from the input energy of 1 kWh? What do you think? We are sure that you're already well aware that knowing how to get a percentage of a number is a valuable ability.

While it's certainly quick and painless just to use our percentage calculator, you don't always have access to a computer or a smartphone. Also, it's just plain cool to be able to perform calculations in your head. Maybe not as cool as juggling flaming torches, but close.

The percentage tells you how number A relates to number B. A real-world example could be: there are two girls in a group of five children. What's the percentage of girls? In other words, we want to know what's the ratio of girls to all children. It's 2 out of 5, or 2/5. We call the first number (2) a numerator and the second number (5) a denominator because this is a fraction. To calculate the percentage, multiply this fraction by 100 and add a percent sign. 100 × numerator / denominator = percentage. In our example, it's 100 × 2/5 = 100 × 0.4 = 40. Forty percent of the group are girls. That's the entire procedure of converting between decimal fractions and percentages.

Do you have problems with simplifying fractions? The best way to solve this is by finding the GCF (greatest common factor) of the numerator and denominator and dividing both of them by GCF.

Let's go the other way around and try to find the numerator. Say we know that 70 percent of fruits in the basket are apples, and there are 30 fruits altogether. It could be worse — they could be lemons. So how many apples do we have? Let's get our percentage formula: 100 × numerator / denominator = percentage. We want to find out the numerator. Let's move all the other parts of the equation to the other side. Divide both sides by 100 (to get rid of 100 on the left) and then multiply both sides by the denominator. This is what we get: numerator = percentage × denominator / 100. Let's substitute percentage and denominator with our values: numerator = 70 × 30 / 100. Now it's easy: numerator = 2100 / 100 = 21, we have 21 apples. Should be enough for lunch or a rather violent food fight.

Now let's solve a problem with an unknown denominator. We spent 30 percent of our pocket money on bubble gum (we never said we're great investors). We bought 12 sticks for $1 each. So we know that $12 was 30 percent of our total budget. How much money did we have before we almost literally blew it all away? Let's start with our formula: 100 × numerator / denominator = percentage or 100 × 12 / denominator = 30. This time we want to find out the denominator. Let's multiply both sides by the denominator and then divide by percentage. This way, we'll get 100 × 12 / 30 = denominator. And the other way around, denominator = 100 × 12 / 30 = 1200 / 30 = 40. We had 40 dollars, and we spent 30 percent, or $12, on bubble gum. Totally worth it.

Staying with our cookie examples, let's name the three parts in our equation: the percentage of cookies — 40%, the whole pack of cookies — 20, and the part of the pack of cookies — 8. Depending on what you want to estimate, you can write three various percentage formulas:

• the equation for percentage is this: percentage = 100 × part / whole, and it answers the question "what percentage of 20 is 8".
• the formula for a part is: part = whole × percentage / 100, and it answers "what is 40% of 20?".
• and finally, the formula for a whole is: whole = 100 × part / percentage, and it says "what is 100% if 8 is 40%?".

That's technically all. You should now know how to find the percentage of a number.

Although Ancient Romans used Roman numerals I, V, X, L, and so on, calculations were often performed in fractions that were divided by 100. It was equivalent to the computing of percentages that we know today. Computations with a denominator of 100 became more standard after the introduction of the decimal system. Many medieval arithmetic texts applied this method to describe finances, e.g., interest rates. However, the percent sign % we know today only became popular a little while ago, in the 20th century, after years of constant evolution.

The term percent is often attributed to Latin per centum, which means by a hundred. Actually, it is wrong. We got the term from Italian per cento — for a hundred. The percent sign % evolved by the gradual contraction of those words over centuries. Eventually, cento has taken the shape of two circles separated by a horizontal line, from which the modern % symbol is derived. The history of mathematical symbols is sometimes astonishing. We encourage you to take a look at the origin of the square root symbol!

Recently, the percent symbol is widely used in programming languages as an operator. Usually, it stands for the modulo operation. On the other hand, in experimental physics, the symbol % has a special meaning. It is used to express the relative error between the true value and the observed value found in a measurement. To know more about relative error, you can check our percent error calculator.

Have you ever met a percent symbol that had an additional circle? That's not a mistake! There are two related signs:

• ‰ — per mille — per thousand,
• ‱ — per myriad — per ten thousand (also known as a basis point),

Later in the text, we explain in more detail what per mille means, what is a basis point and how to convert per milles and basis points to percents.

Higher proportions use other notation (called parts-per notation), e.g., parts-per-million (PPM) which is frequently used to measure the concentration of a substance in solution or mixture. Of current concern is smog, the tiny particulate matter that enters the air and can seriously affect someone's health.

Percent or per cent? It depends on your diet. If you eat hamburgers for the majority of your meals, it is percent. If you prefer fish and chips, it is per cent. If you spray your fish-smelling chips with vinegar, then it is per cent, mate (as opposed to burger eaters' percent, dude). When it comes to percentage, both sides of the pond are in agreement: it should be a single word. Still confused? Americans say percent, British use per cent. Something tells us that American English is more popular nowadays, so this website uses a single-word form.

Per mille, per mil, per mill, or simply ‰ is similar to percent, only it is one thousandth (1/1000 or 0.001). If our household's budget is $2400 and we allocated 1 per mille of that to buying chewing gum, we would spend 2.4 dollars (2 dollars 40 cents) on annoying our teachers (well, 20 years ago it was not allowed in Polish schools. We do not know the rules nowadays 😃). It's pretty similar to how you find percentages. If you wanted to use percentage calculator to count per mille, simply use numbers 10× lower (0.2 instead of 2, 4 instead of 40).

Per myriad, basis point or just ‱ is one ten-thousandth(1/10000 or 0.0001). It's 10× smaller than per mille, so to convert basis points to percents, you need to divide them by 100. It's that simple!

Percentage points (or percent points) are a rather tricky beast. We use it all the time even if we don't know it — and in these situations, we often incorrectly say percent instead of a percentage point. Once you read this section, you will know how to do it properly and be annoyed for the rest of your life (because other people will keep making the mistake).

Senator Homer Simpson was polling at 10% last month. He had a few successful debates since then, and now 12% of the population wants to vote for him. What's the change? You want to say 2%, are we right? It's wrong! Let's examine this. Imagine the whole population is 1000 people. 10% of them is 100. 12% is 120. What's the percentage increase? It's 100 × 20 / 100 = 20%!

This situation is when percentage points come in handy. We use percentage points when we want to talk about a change from one percentage to another. A change from 10% to 12% is two percentage points (or 20 percent).

Understanding changes in percentages can be done in two different ways:

• Change in percentage points (pp): The difference between two percentage values. If one value is 10 % and the other is 30 %, the change is 20 percentage points (20 pp).
• Change in percentage: The relative change between two percentage values. If one value is 10 % and the other is 30 %, the change is 200 % of the original 10 %.

Now, when you know everything about percentage points, we guarantee that you will read or hear other people incorrectly saying percent when they should be using percentage points. If you're anything like us, you will scream at the newspaper, insulting it in some made-up language. This reaction helps to free up space around you when you're using public transportation :-)

Mateusz and Dominik are experienced in creating scientific tools that solve everyday problems and explaining the concepts in a simple, easy-to-digest manner. The idea for this percentage calculator was born when Mateusz was shopping online and comparing prices and discount percentages on different websites. Now, they use it not just to make better shopping decisions but to pick better investments.

We put extra care into the quality of the content to ensure they are as accurate and reliable as possible. Each tool is peer-reviewed by a trained expert and then proofread by a native speaker. If you’d like to learn more about our standards, please check the Editorial Policies page.